Эконометрика. Решение. Вес (унция)Y
 Скачать 1.01 Mb.
|
|
Задача № 14
На основании следующей информации по 10 магазинам построить линейную модель связи между прибылью и оборотом. Пояснить смысл параметров уравнения регрессии. Рассчитайте прогнозное значение результата (Р=75%), если прогнозные значения фактора Х составят 85% от его максимального значения. Результаты моделирования и прогнозирования отобразить на графике. Используя построенную модель, ранжировать магазины по степени их эффективности. Решение: Построим уравнение парной регрессии. Линейное уравнение регрессии имеет вид:  Итак, для того, чтобы вывести линейное уравнение регрессии для зависимости затрат на рекламу (У) от количества туристов (Х), определим параметры 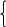 . Для этого решим систему уравнений с двумя неизвестными.  n0 +1x =y 0x +1x2 =xy Для расчета параметров а и b линейной регрессии методом наименьших квадратов необходимо решить систему нормальных уравнений относительно а и b: 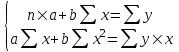 Для расчета параметров уравнения линейной регрессии строим расчетную таблицу 7.1. Значения параметров а и b линейной модели можно определить по формулам: 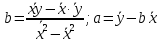 Составим расчетную таблицу: Таблица 14.1
Определим значения параметров а и b линейной модели, используя данные таблицы 14.1. 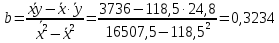 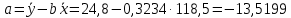 Уравнение регрессии будет иметь вид: 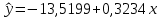 Коэффициент регрессии b = 0,3234 показывает среднее изменение результативного показателя (годовой прибыли) с повышением или понижением величины фактора х (оборота розничной торговли ) на единицу его измерения. Таким образом, с увеличением оборота розничной торговли на 1 тыс.$ годовая прибыль магазинов увеличивается в среднем на 0,3234 тыс.$. Коэффициент a = -13,52 формально показывает прогнозируемый уровень у, но только в том случае, если х=0 находится близко с выборочными значениями. Для расчета параметров уравнения регрессии можно воспользоваться пакетом MS Excel: Анализ данных, инструмент Регрессия. 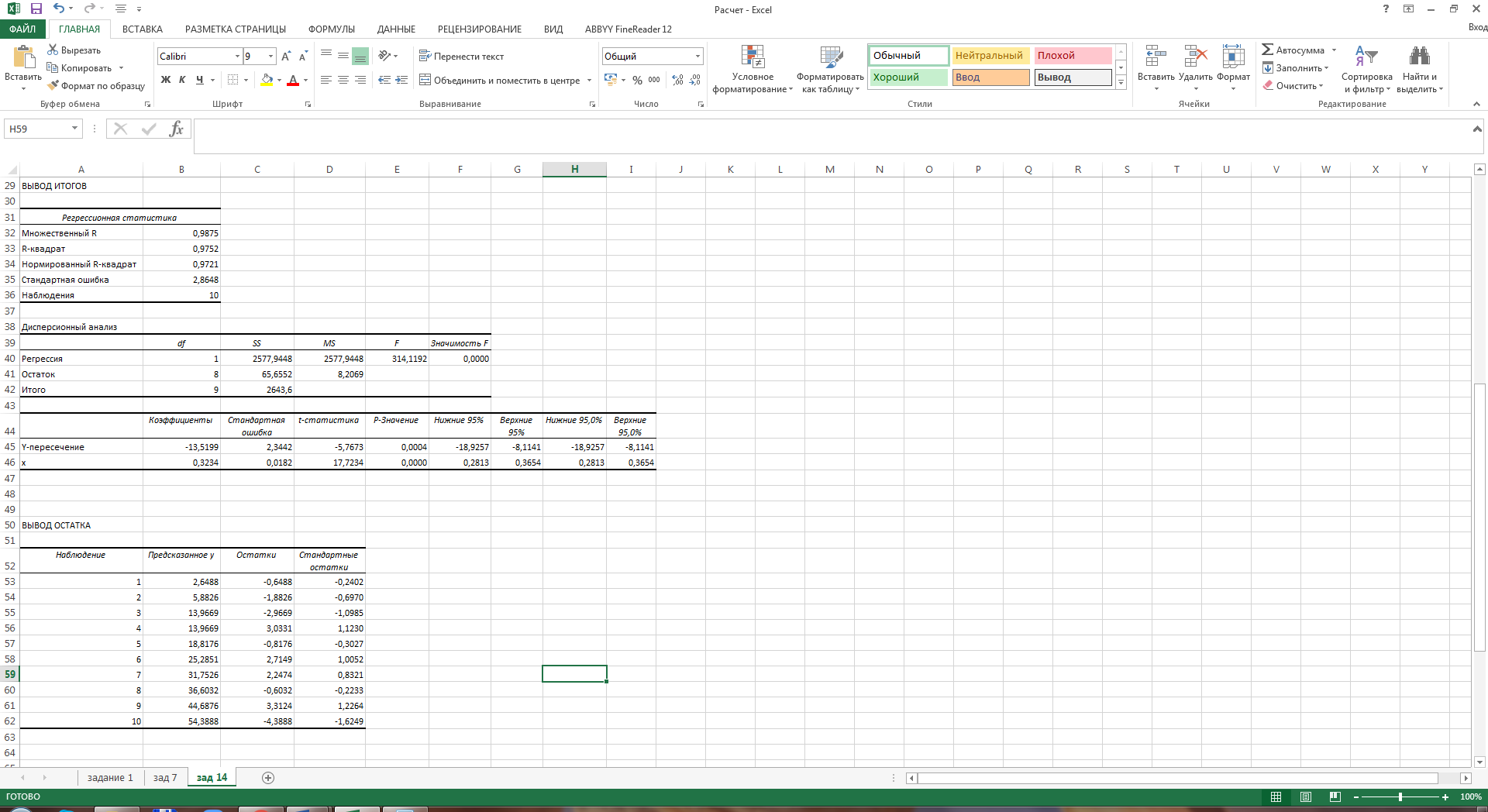 Рис.14.1 Рассчитаем прогнозное значение результата (Р=75%), если прогнозные значения фактора Х составят 85% от его максимального значения. Максимальное значение оборота торговли равно 210. Тогда прогнозное значение оборота составит: 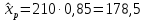 Прогнозное значение годовой прибыли будет равно: 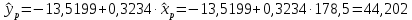 Оценим точность прогноза, рассчитав ошибку прогноза и его доверительный интервал. Средняя квадратическая ошибка прогноза находится по формуле: 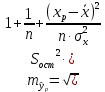 где: 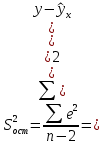 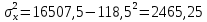 Ошибка прогноза составит: 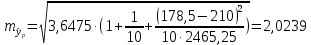 Табличное значение 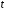 -критерия для числа степеней свободы: df = n -2 =11 - 2 = 9 и α = 0,15 составит tтабл = 1,574.Предельная ошибка прогноза, которая в 85% случаев не будет превышена, составит: 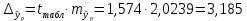 Доверительный интервал прогноза: 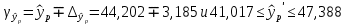 Выполненный прогноз годовой прибыли является надежным (p = 1 – α = 1 – 0,15 = 0,85) и находится в пределах от 41,017 тыс.$ и до 47,388 тыс.$. Результаты моделирования и прогнозирования отобразиv на графике. 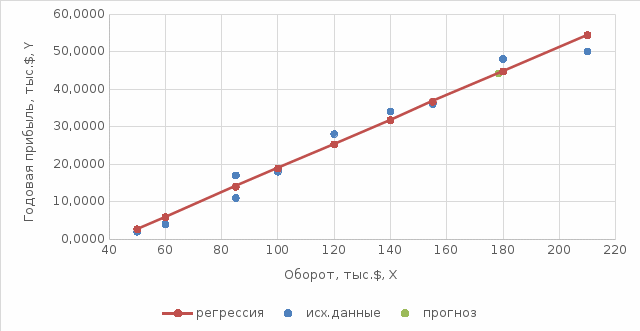 Рис.14.2 Используя построенную модель, ранжируем магазины по степени их эффективности. Для определения лучшей компании при его прибыли лучше делать ранжирование по остаткам. Таблица 14.2 – Ранжирование по остаткам
Эффективными будут компании, остатки которых будут положительными, при этом, если стандартизированный остаток больше или близок к 2, то компании очень эффективные. Неэффективными будут магазины, остатки которых будут отрицательными, при этом, если стандартизированный остаток меньше или близок к −2, то магазины откровенно убыточные с неэффективным управлением. Наиболее эффективные магазины выделены красным цветом, самые худшие – желтым цветом. |
