Эконометрика. Решение. Вес (унция)Y
 Скачать 1.01 Mb.
|
|
Решение системы можно найти по формулам Крамера либо можно найти по следующим формулам: 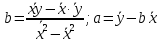 Получим: 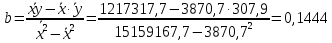 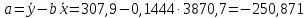 Уравнение линейной парной регрессии будет иметь вид: 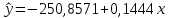 Определим параметры уравнения с помощью пакета Анализ данных средства MS Excel (инструмент Регрессия) (Рис.20.1). 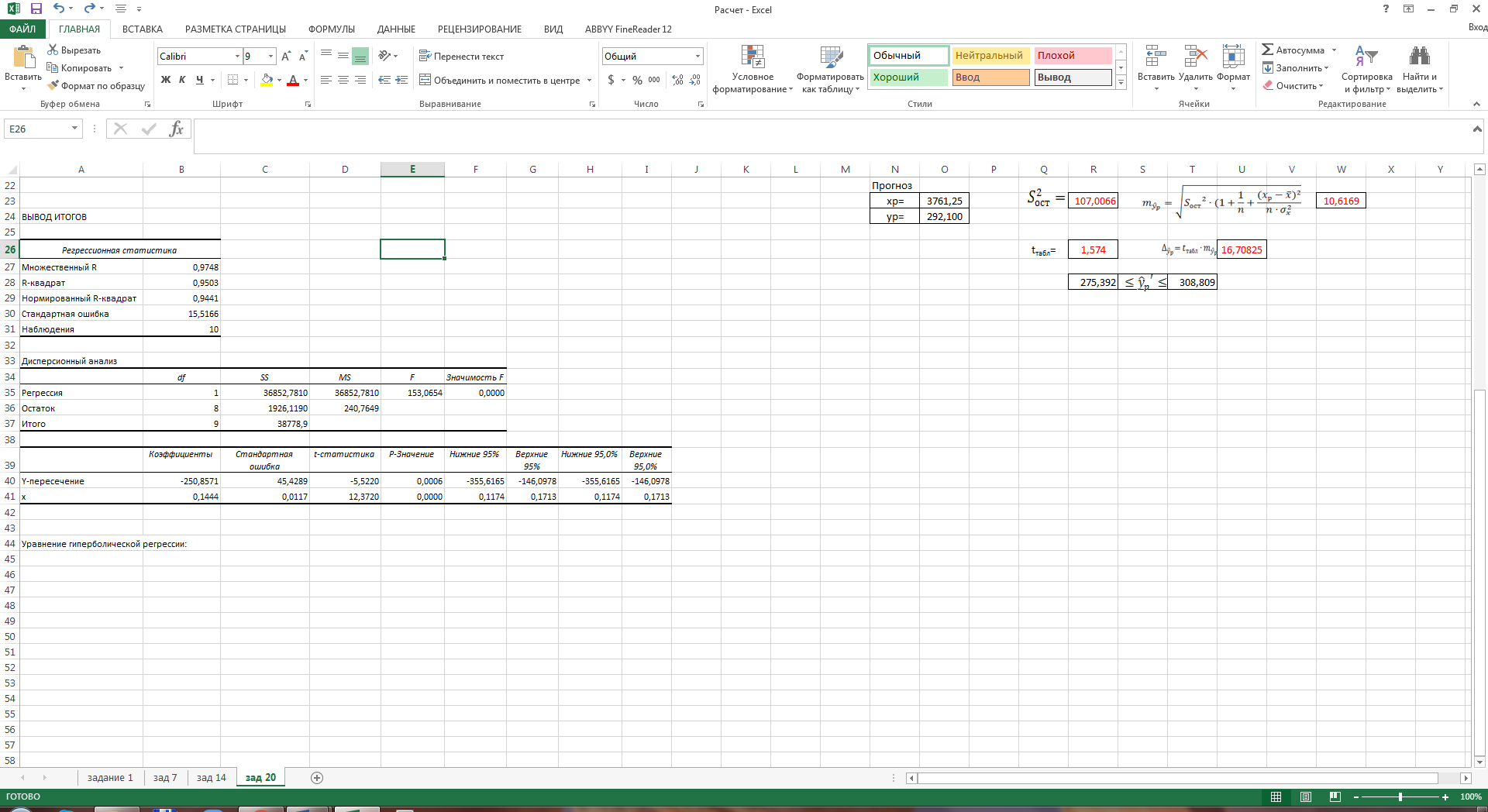 Рис.20.1 Уравнение линейной парной регрессии имеет вид: 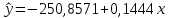- уравнение гиперболической регрессии имеет вид: 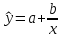 Произведем линеаризацию модели путем замены 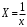 . 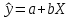В результате получим линейное уравнение: Строим вспомогательную таблицу: Таблица 20.2
Параметры уравнения можно определить по формулам: 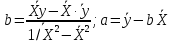 Имеем: 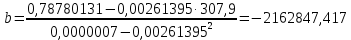 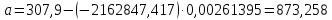 Тогда уравнение гиперболической регрессии с учетом замены переменной имеет вид: 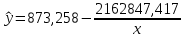 Определим параметры уравнения с помощью пакета Анализ данных средства MS Excel (инструмент Регрессия) (Рис.20.2). 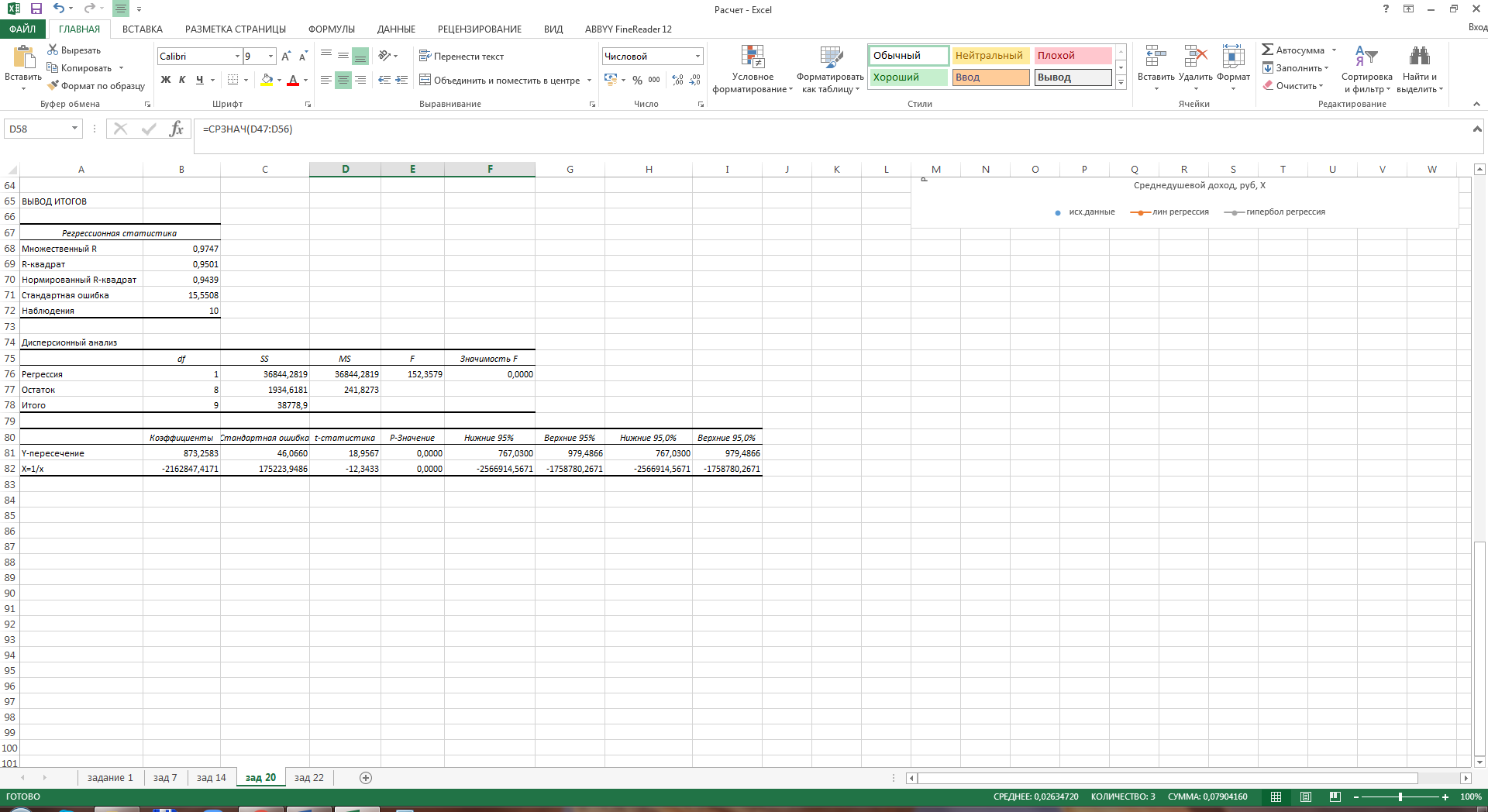 Рис.20.2 Как видно из протокола регрессионного анализа, параметры уравнения рассчитаны верно. Для анализа полученных уравнений регрессионных моделей произведем дополнительные расчеты. Оценим тесноту связи с помощью показателей корреляции и детерминации. Для линейной модели Тесноту линейной связи оценит коэффициент корреляции, который вычисляется по формуле: 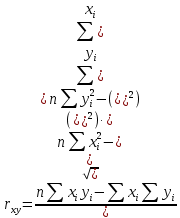 Коэффициент корреляции можно найти с помощью статистической функции КОРРЕЛ(): 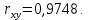 Значение коэффициента корреляции также можно взять из протокола регрессионного анализа (рис.20.1): rxy= 0,9748. Можно сказать, что связь между y (расходами на оздоровительные услуги) и фактором x (среднедушевым доходом) прямая и полная. Определим коэффициент детерминации R2: 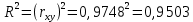 Вариация результата у (расходы на оздоровительные услуги) на 95,03% объясняется вариацией фактора х (среднедушевой доход). Для гиперболической модели Оценим тесноту связи с помощью показателя корреляции по данным таблицы 20.2. Показателем корреляции для нелинейной регрессии является индекс корреляции: 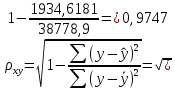 Можно сказать, что связь между y (расходами на оздоровительные услуги) и фактором x (среднедушевым доходом) прямая и полная. Индекс детерминации вычислим по формуле: 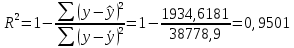 Вариация результата у (расходы на оздоровительные услуги) на 95,03% объясняется вариацией фактора х (среднедушевой доход). Остальные 4,97% объясняются другими факторам, не входящими в модель. По протоколу регрессионного анализа, значения коэффициента корреляции и детерминации такие же, как рассчитанные выше. Для оценки статистической значимости уравнения регрессии используется критерий Фишера. Если фактическое значение критерия Фишера больше табличного, то уравнение статистически значимо, если наоборот, то уравнение статистически не значимо. Линейная регрессия Рассчитаем значение F-критерия Фишера: 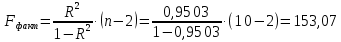 Т.к. Fфакт = 153,07 > Fтабл = 5,59 для α=0,05; к1 = m = 1, к2 = n – m – 1 = 7, то уравнение регрессии с вероятностью 0,95 в целом статистически значимо. Гиперболическая регрессия 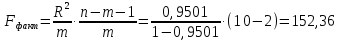 Т.к. Fфакт = 152,36 > Fтабл = 5,59 для α=0,05; к1 = m = 1, к2 = n – m – 1 = 7, то уравнение регрессии с вероятностью 0,95 в целом статистически значимо.. Для анализа полученных уравнений регрессионных моделей этого построим сводную таблицу результатов. Таблица 20.3
Если рассматривать характеристики моделей по коэффициенту корреляции, детерминации и значению F- критерия Фишера, то обе модели практически одинаковые значения. То есть обе модели хорошие и статистически значимы. Представитм обе модели в графическом виде. 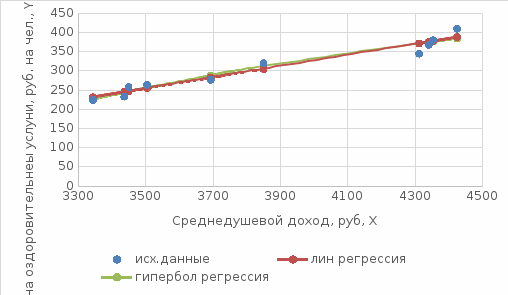 Рис.20.3 На базе линейной модели найти оценку расходов на ближайший месяц (Р=75%). Построим с помощью линейного тренда в MS Excel прогноз на 1 период вперед: 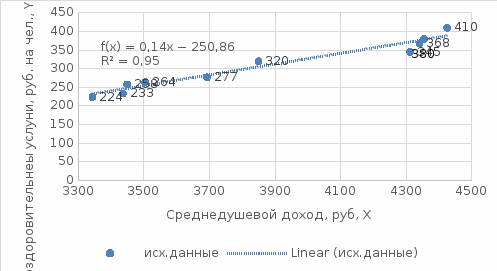 Рис.20.4 Как видно из линии тренда значение расходов будет находиться в границах от 380 до 410 руб. на человека. Задача № 22 В таблице представлены данные о цене двухкомнатных квартир на вторичном рынке жилья в областном центре (Y, млн. руб.), общей площади квартир (X1, м2), площади кухни (X2, м2).
Требуется построить модель множественной регрессии, оценить качество модели. Оценить точность модели с помощью средней относительной ошибки аппроксимации. Ответить на вопрос: целесообразно ли упрощение модели с отбрасыванием одного из факторов? Решение: Уравнение множественной регрессии имеет вид: 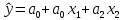 Для определения его параметров уравнения, воспользуемся пакетом Анализ данных, инструмент Регрессии программного средства MS Excel. 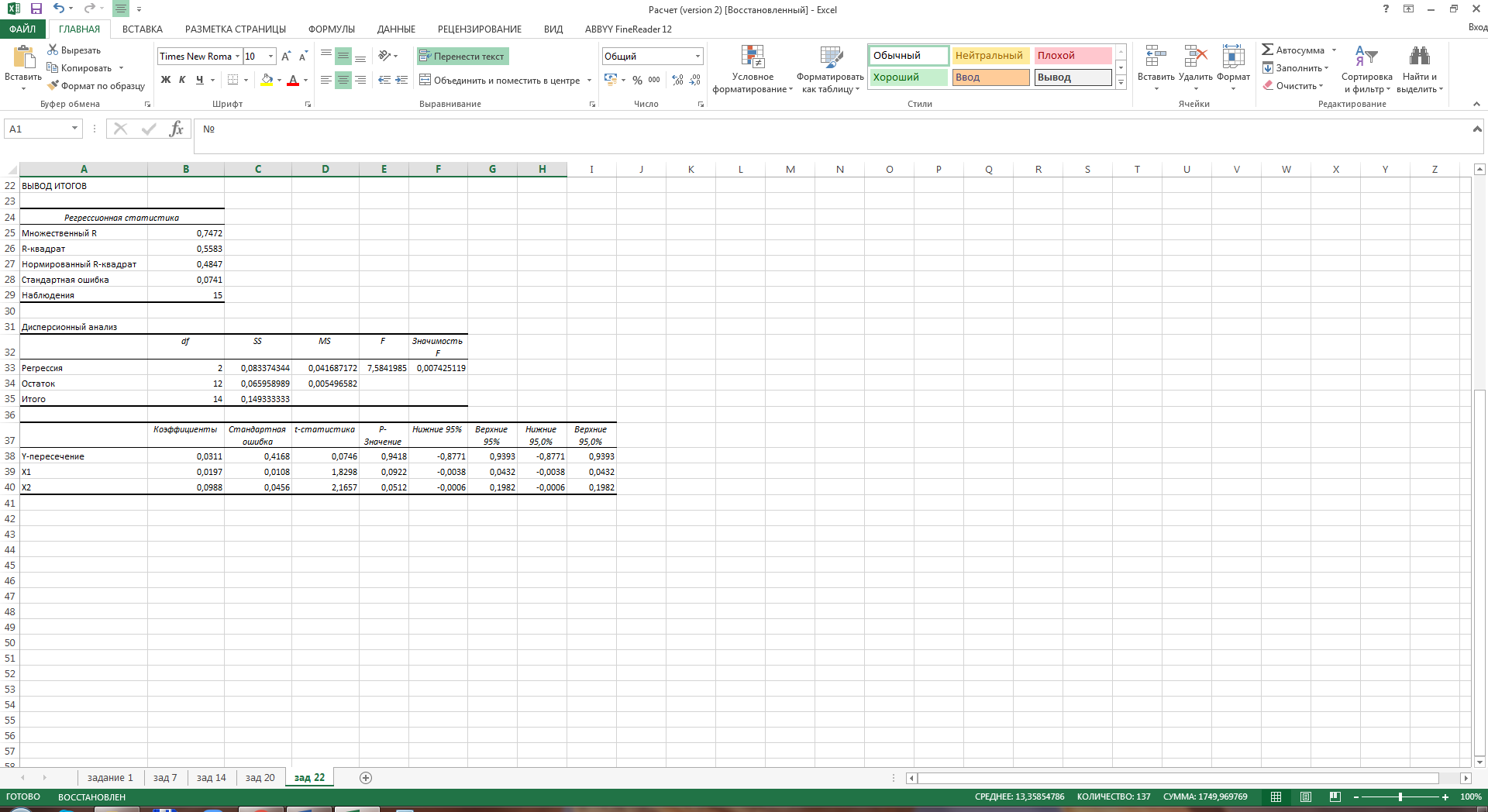 Рис.22.1 Построенная модель прогноза имеет вид: 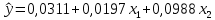 Интерпретация параметров модели: параметр 0,0197 показывает, при увеличении общей площади квартиры (х1) на 1 кв.м.. (при неизменном х2) цена двухкомнатной квартиры (y) увеличится в среднем на 0,0197 млн.руб.., а при увеличении площади кухни (х2) на 1 кв.м.. (при неизменном х1) цена квартиры (y) увеличится в среднем на 0,0988 млн.руб. Произведем дополнительные расчеты в Таблице 22.1 Таблица 22.1
Рассчитаем индекс множественной корреляции по формуле: 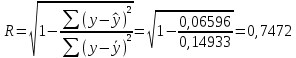 Индекс множественной детерминации равен: 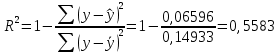 Рассчитаем значение F-критерия по формуле: 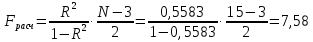 Табличное значение Фишера при вероятности α = 0,05, с двумя числами степеней свободы (2 и N – 3 = 15 - 3 = 12): Fтабл = 3,885. Сравним фактическое и расчетное Fрасч значения: 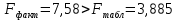 Т.к. Fфакт > Fтабл , следовательно, уравнение регрессии статически значимо. Оценим качество уравнения через среднюю ошибку аппроксимации, которая определяется по формуле: 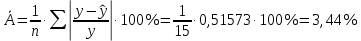 Таким образом, фактические значения результативного признака отличаются от теоретических значений на 3,44%. Качество построенной модели оценивается как хорошее, т.к. меньше 10%. Рассчитаем частные критерии Фишера по формулам: 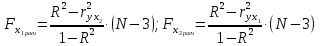 Определим частные коэффициенты корреляции с помощью инструмента Корреляция в MS Excel:
Таким образом, мы имеем: 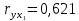 ;  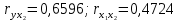Частные критерии Фишера будут равны: 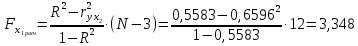 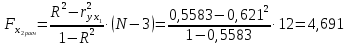 Получили, что: 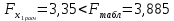 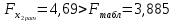 Результаты позволяют сделать вывод: 1) о незначимости фактора х1 и нецелесообразности включения его в уравнение регрессии после фактора х2; 2) о значимости фактора х2 и целесообразности включения его в уравнение регрессии после фактора х1. Задача № 27 Известна зависимость между пробегом автомобилей Х (тыс. км) и стоимостью ежемесячного обслуживания Y (тыс. руб.): Y=10,551+1,043X и известен ряд остатков:
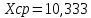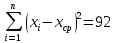  Коэффициент парной корреляции r(x,y) = 0,906 На основании приведенных данных требуется оценить качество модели регрессии с помощью коэффициента детерминации, проверить значимость уравнения регрессии (критерий Фишера). Определить прогнозные значения стоимости ежемесячного обслуживания, если пробег составит 18 тыс.км (Р=85%). Решение: Оценим качество модели регрессии: Коэффициент детерминации равен: 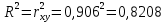 С помощью 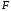 -критерия Фишера оценим статистическую значимость уравнения регрессии с надежностью 0,95.F-критерий состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера Фактическое значение 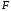-критерия согласно протокола регрессионного анализа равно: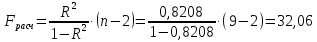 Табличное значение критерия при 0,05%-ном уровне значимости и степенях свободы k1 =1 и k2 = 9 – 2 = 7 составляет Fтабл = 5,59. Т.к. неравенство Fрасч = 32,06 > Fтабл = 5,59 выполняется, поэтому гипотеза H0 отклоняется и признается статистическая значимость уравнения. 2. Определим прогнозные значения стоимости ежемесячного обслуживания, если пробег составит 18 тыс.км (Р=85%). Прогнозное значение стоимости ежемесячного обслуживания при пробеге 18 тыс.км. будет равно: 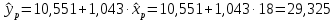 Оценим точность прогноза, рассчитав ошибку прогноза и его доверительный интервал. Средняя квадратическая ошибка прогноза находится по формуле: 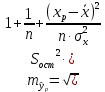 где: 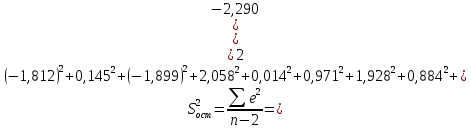 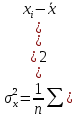 где: 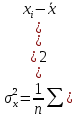выборочная дисперсия переменной x. Ошибка прогноза составит: 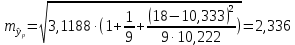 Табличное значение 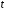 -критерия для числа степеней свободы: df = n -2 =9 - 2 = 7 и α = 0,15 составит tтабл = 1,617.Предельная ошибка прогноза, которая в 85% случаев не будет превышена, составит: 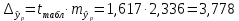 Доверительный интервал прогноза: 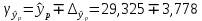 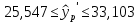 Выполненный прогноз стоимости ежемесячного обслуживания припробеге в 18 тыс.км. является надежным (p = 1 – α = 1 – 0,15 = 0,85) и находится в пределах от 25,547 тыс.руб. и до 33,103388 тыс.руб. |
