Эконометрика. Решение. Вес (унция)Y
 Скачать 1.01 Mb.
|
|
Задача № 1 Исследуется зависимость веса куриных окорочков от возраста кур и страны производителя. Требуется выяснить, как вес куриных окорочков зависит от возраста кур и страны производителя.
1. Построить линейное уравнение регрессии. Дать экономическую интерпретацию коэффициентов модели. 2. Оценить качество полученного уравнения. 3. Построить графики частных уравнений регрессии. Решение: 1. Построим линейное уравнение регрессии Общий вид линейного уравнения с фиктивной переменной: Построим уравнение множественной регрессии следующего вида: 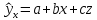 Z – фиктивная переменная, которую введем согласно правила: 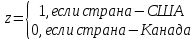 Для нахождения параметров линейного уравнения множественной регрессии воспользуемся инструментом Регрессия Пакета анализа Microsoft Excel. 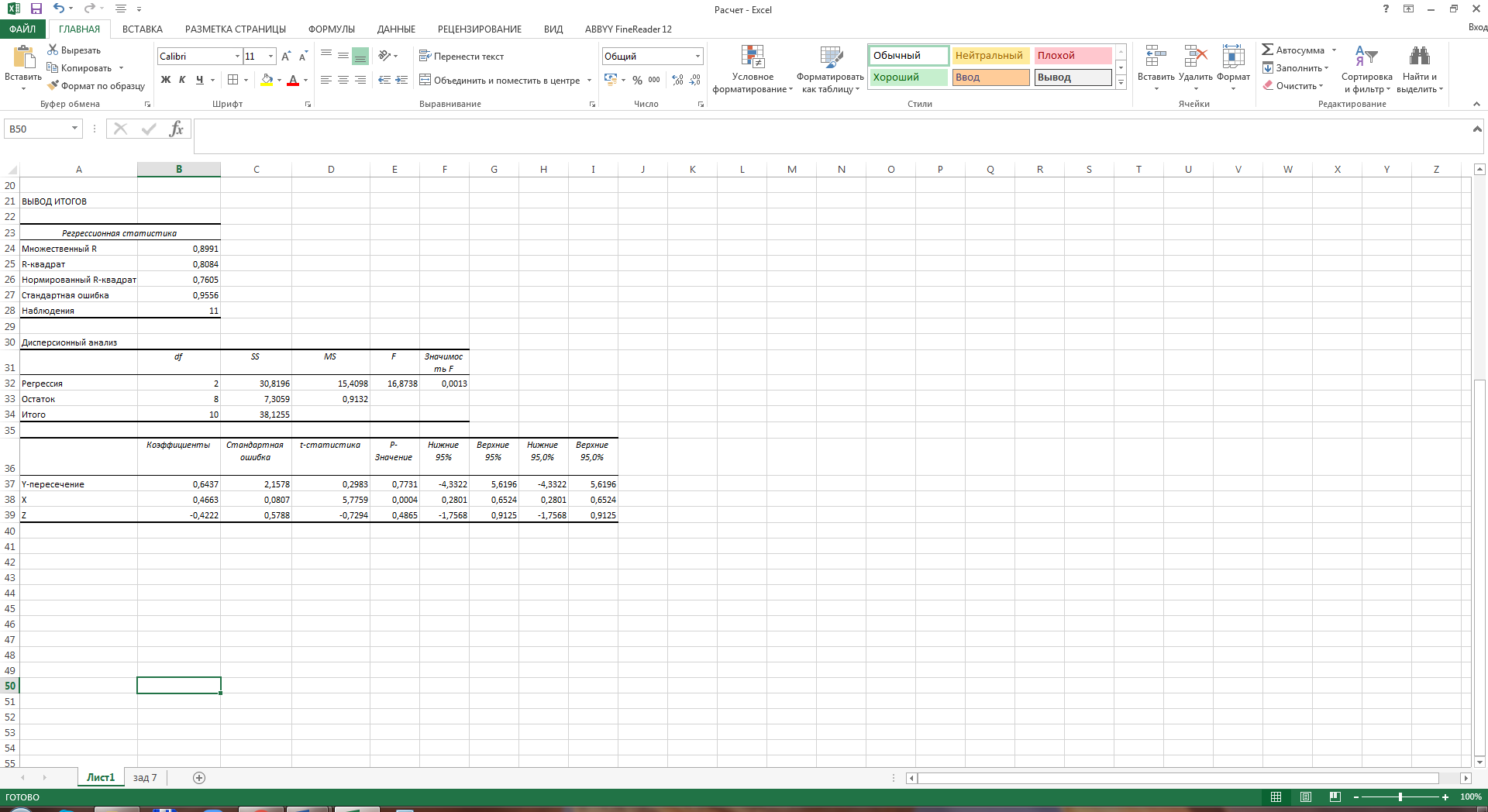 Рис.1.1 Результат регрессионного анализа Таким образом, линейное уравнение множественной регрессии, выражающее зависимость веса куриных окорочков от возраста кур и страны производителя имеет вид: 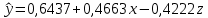 Таким образом, вес куриных окорочков из США (z=1) определяется с помощью уравнения: 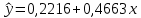 из Канады (z=0): 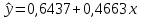 Коэффициенты уравнения говорят о том, что с повышением возраста курицы на 1 месяц, вес окорочка увеличивается на 0,4663 унции . При этом окорочка из США в среднем на 0,4222 унции меньше, чем окорочка куриц того же возраста из Канады. 2. Оценим качество полученного уравнения. Коэффициент множественной детерминации – это доля объясняющей дисперсии экзогенной переменной в её общей дисперсии. В нашем случае, коэффициент множественной детерминации равен 0,8084, что говорит о том, что 80,84% вариации результата (веса окорочка) объясняется вариацией представленных в уравнении факторов (возрастом курицы и производителем), то есть уравнение регрессии достаточно объясняет вариацию объёма продаж. При этом окорочка из США в среднем на 0,4222 унции меньше, чем окорочка куриц того же возраста из Канады. С помощью 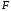 -критерия Фишера оценим статистическую значимость уравнения регрессии с надежностью 0,95.F-критерий состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера Фактическое значение 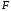-критерия согласно протокола регрессионного анализа равно: 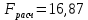 Табличное значение критерия при 0,05%-ном уровне значимости и степенях свободы k1 =1 и k2 = 11 – 2 = 9 составляет Fтабл = 5,118. Т.к. неравенство Fрасч = 16,87 > Fтабл = 5,118 выполняется, поэтому гипотеза H0 отклоняется и признается статистическая значимость уравнения. 3.Построим графики частных уравнений регрессии Частное уравнение регрессии по фактору Х имеет вид: 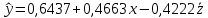 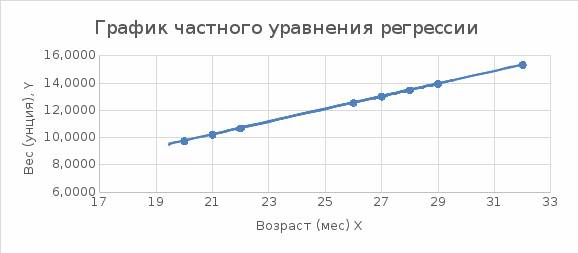 Рис.1.2 Частное уравнение регрессии по фактору Z имеет вид: 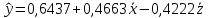 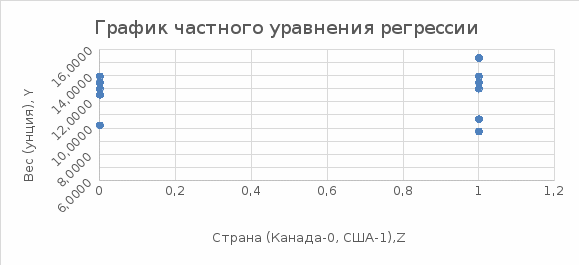 Рис.1.3 Задача № 7 Имеется 20 фирм, по каждой из которых известны данные о затратах на рекламу сервиса и о количестве туристов, воспользовавшихся услугами фирмы
Требуется: 1) построить уравнение парной регрессии; 2) проверить качество построенного уравнения; 3) выполнить прогноз количества туристов (Р=85%), если затраты на рекламу в ближайшем периоде увеличатся на 7% от её максимального значения (результаты отобразить на графике). Решение: Построим уравнение парной регрессии. Линейное уравнение регрессии имеет вид:  Итак, для того, чтобы вывести линейное уравнение регрессии для зависимости затрат на рекламу (У) от количества туристов (Х), определим параметры 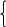 . Для этого решим систему уравнений с двумя неизвестными.  n0 +1x =y 0x +1x2 =xy Для расчета параметров а и b линейной регрессии методом наименьших квадратов необходимо решить систему нормальных уравнений относительно а и b: 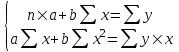 Для расчета параметров уравнения линейной регрессии строим расчетную таблицу 7.1. Значения параметров а и b линейной модели можно определить по формулам: 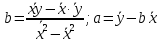 Составим расчетную таблицу: Таблица 7.1.
Определим значения параметров а и b линейной модели, используя данные таблицы 7.1. 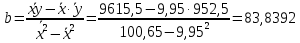 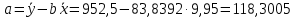 Уравнение регрессии будет иметь вид: 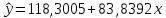 Коэффициент регрессии b = 83,84 показывает среднее изменение результативного показателя (количество туристов) с повышением или понижением величины фактора х (затраты на рекламу) на единицу его измерения, те.е.с увеличением на 1 единицу затрат на рекламу количество туристов повышается в среднем на 83,84. Коэффициент a = 118,3 формально показывает прогнозируемый уровень у, но только в том случае, если х=0 находится близко с выборочными значениями. Проверим качество построенного уравнения. Тесноту линейной связи оценит коэффициент корреляции, определяемый по формуле: 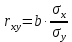 где: σx σy – среднеквадратичные отклонения. Рассчитываются по формулам: 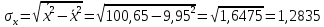 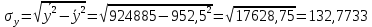 Тогда коэффициент корреляции будет равен: 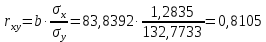 Значение коэффициента корреляции показывает, что линейная связь между признаками прямая и высокая. Рассчитаем коэффициент детерминации: 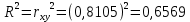 Таким образом, в 65,69 % случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - средняя. Остальные 34.31 % изменения Y объясняются факторами, не учтенными в модели (а также ошибками спецификации). Выполним прогноз количества туристов (Р=85%), если затраты на рекламу в ближайшем периоде увеличатся на 7% от её максимального значения. Подставив в уравнение регрессии соответствующие значения х, можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения. Максимальное значение затрат на рекламу равно 12. Тогда прогнозное значение затрат на рекламу составит: 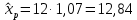 Прогнозное значение количества туристов при Х = 12,84 (составит: 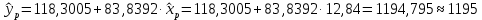 Оценим точность прогноза, рассчитав ошибку прогноза и его доверительный интервал. Средняя квадратическая ошибка прогноза находится по формуле: 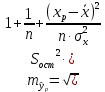 где: 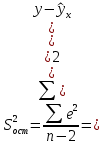 Ошибка прогноза составит: 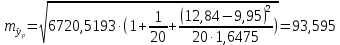 Табличное значение 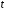 -критерия для числа степеней свободы: df = n -2 =11 - 2 = 9 и α = 0,15 составит tтабл = 1,574.Предельная ошибка прогноза, которая в 85% случаев не будет превышена, составит: 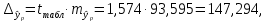 Доверительный интервал прогноза: 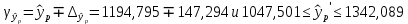 Выполненный прогноз количества туристов является надежным (p = 1 – α = 1 – 0,15 = 0,85) и находится в пределах от 1048 до 1342 туристов. Отобразим полученные данные на графике: 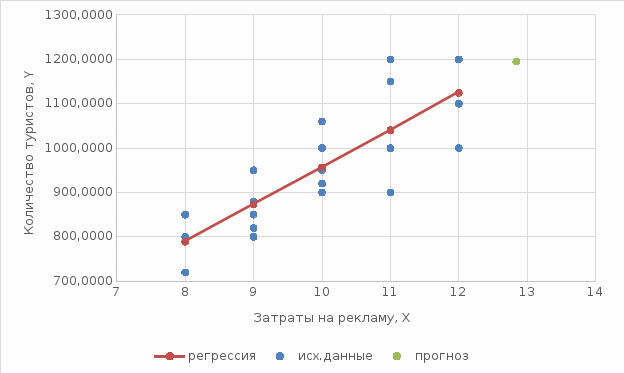 Рис.7.1 |
