Выбор формы уравнения регрессии
 Скачать 8.7 Mb.
|
|
7. Проверка значимости коэффициента корреляции и коэффициента детерминации Коэффициент корреляции В качестве меры тесноты взаимосвязи используется коэффициент корреляции: r =  =  , (18)где σx = , σy = . Вычисление коэффициента корреляции по формуле (5) является трудоемкой операцией. Выполнив несложные преобразования, можно получить следующую формулу для расчета линейного коэффициента корреляции:  (19)Линейный коэффициент корреляции может принимать любые значения в пределах от минус 1 до плюс 1. Чем ближе коэффициент корреляции по абсолютной величине к 1, тем теснее связь между признаками. Знак при линейном коэффициенте корреляции указывает на направление связи - прямой зависимости соответствует знак плюс, а обратной зависимости – знак минус. Коэффициент детерминации При анализе качества модели регрессии, в первую очередь, используется коэффициент детерминации, который определяется следующим образом: 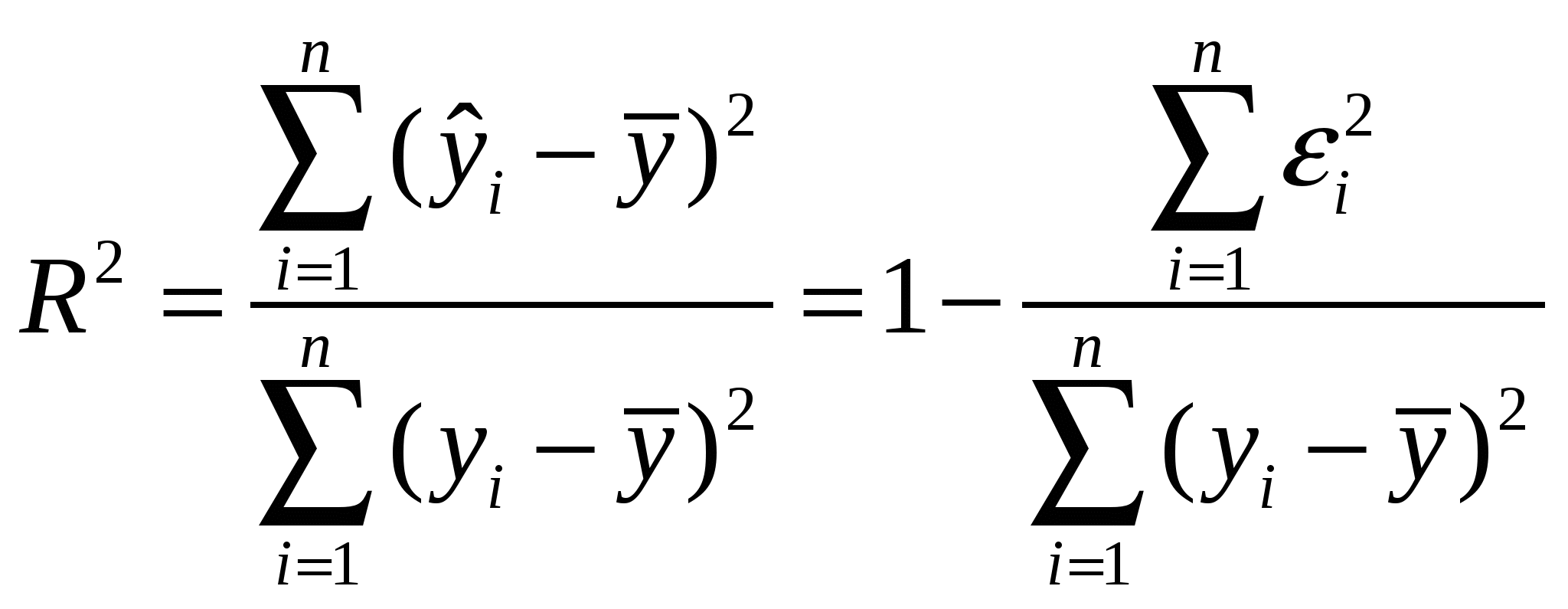 , (2.5)где  - среднее значение зависимой переменной, - предсказанное (расчетное) значение зависимой переменной.Коэффициент детерминациипоказывает долю вариации результативного признака, находящегося под воздействием изучаемых факторов, т. е. определяет, какая доля вариации признака Y учтена в модели и обусловлена влиянием на него факторов. Чем ближе  к 1, тем выше качество модели.Для проверки значимости модели Для проверки значимости модели регрессии используется F-критерий Фишера. Если расчетное значение с 1= k и 2 = (n - k - 1) степенями свободы, где k – количество факторов, включенных в модель, больше табличного при заданном уровне значимости, то модель считается значимой. 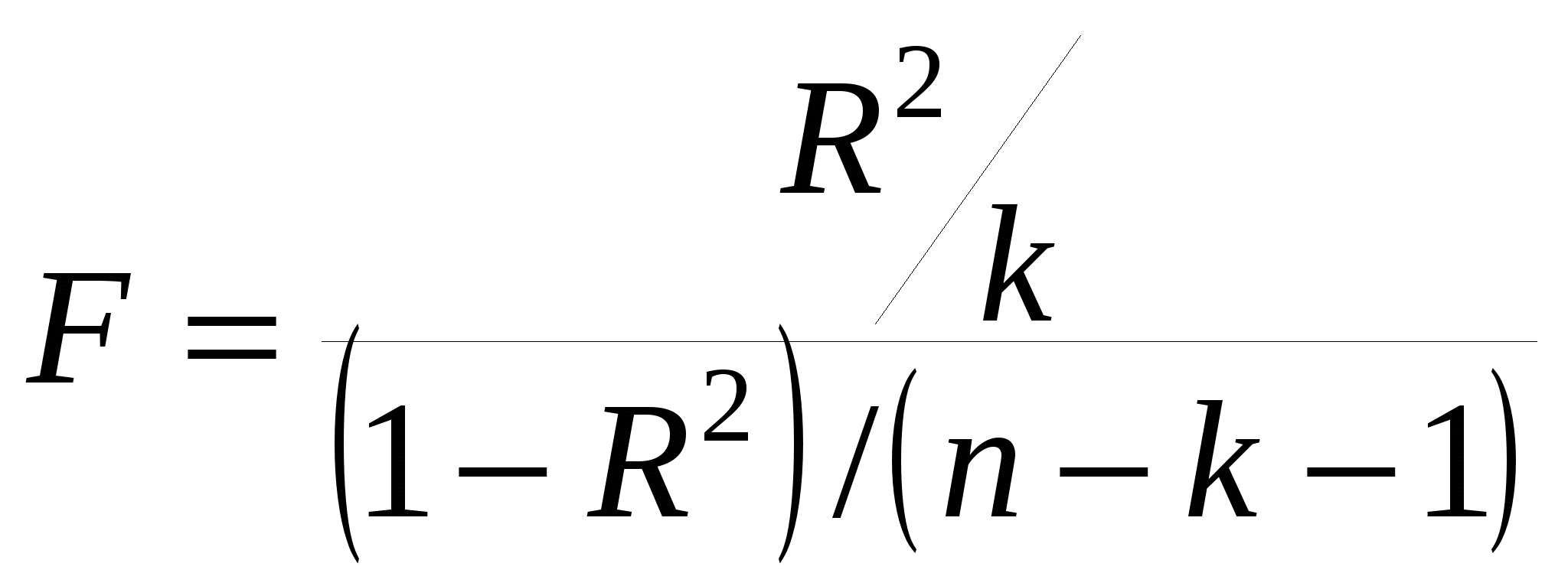 (2.7) В качестве меры точности применяют несмещенную оценку дисперсии остаточной компоненты, которая представляет собой отношение суммы квадратов уровней остаточной компоненты к величине (n- k -1), где k – количество факторов, включенных в модель. Квадратный корень из этой величины ( 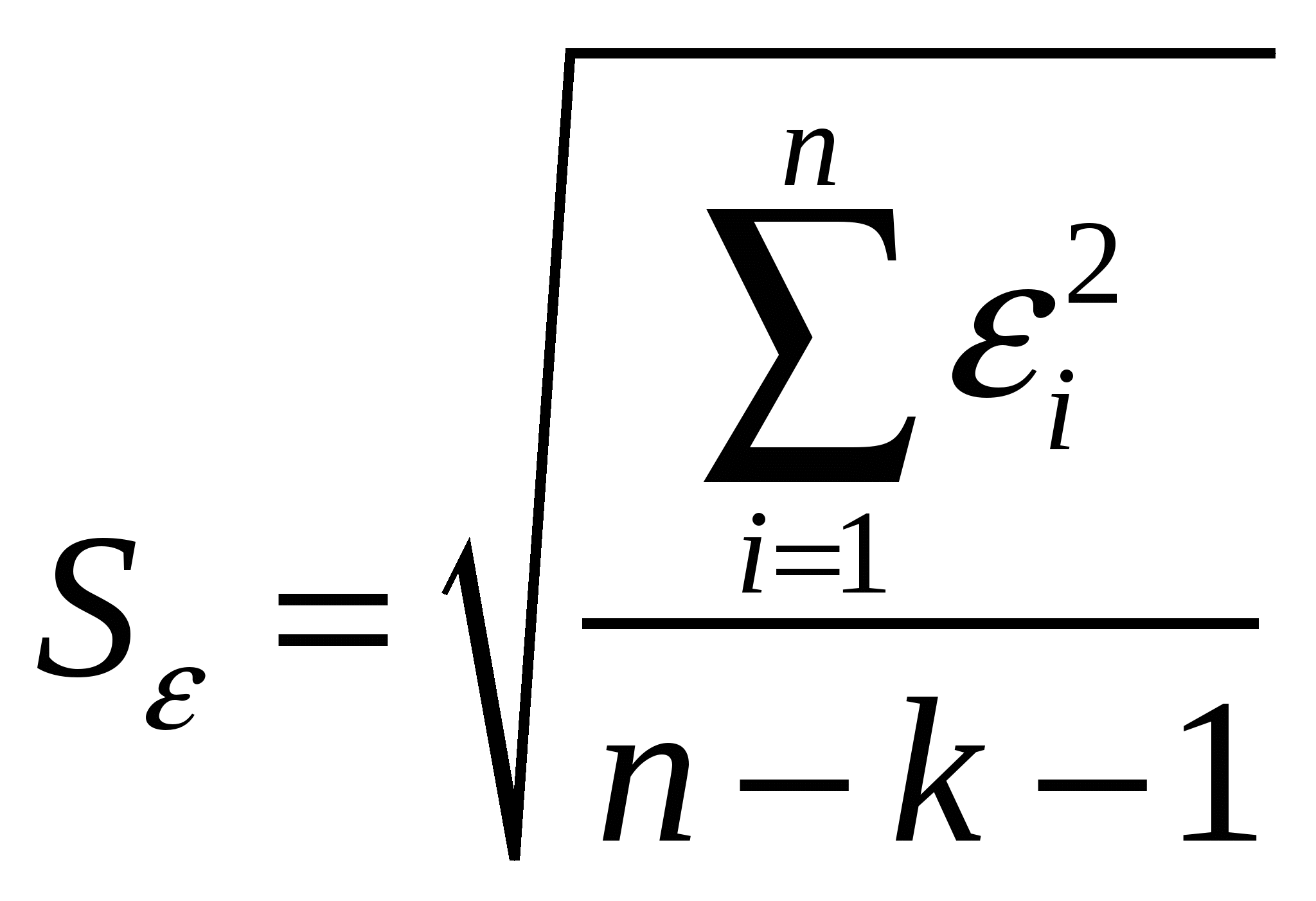 ) называется стандартной ошибкой: (2.8)значимость отдельных коэффициентов регрессии проверяется по t-статистике путем проверки гипотезы о равенстве нулю j-го параметра уравнения (кроме свободного члена):  , (2.9)где Saj— это стандартное (среднеквадратическое) отклонение коэффициента уравнения регрессии aj.Величина Saj представляет собой квадратный корень из произведения несмещенной оценки дисперсии  и j -го диагонального элемента матрицы, обратной матрице системы нормальных уравнений. где  - диагональный элемент матрицы  .Если расчетное значение t-критерия с (n - k - 1) степенями свободы превосходит его табличное значение при заданном уровне значимости, коэффициент регрессии считается значимым. В противном случае фактор, соответствующий этому коэффициенту, следует исключить из модели (при этом ее качество не ухудшится). 8. Оценка существенности параметров линейной регрессии и корреляции. Корреляционный и регрессионный анализ обычно проводится для ограниченной по объёму совокупности. Поэтому показатели регрессии и корреляции - параметры уравнения регрессии, коэффициенты корреляции и детерминации могут быть искажены действием случайных факторов. Чтобы проверить, насколько эти показатели характерны для всей генеральной совокупности, не являются ли они результатом стечения случайных обстоятельств, необходимо проверить адекватность построенных статистических моделей. После построения уравнения линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров. Проверить значимость уравнения регрессии - значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной. Методы оценки тесноты связи подразделяются на корреляционные (параметрические) и непараметрические. Параметрические методы основаны на использовании, как правило, оценок нормального распределения и применяются в случаях, когда изучаемая совокупность состоит из величин, которые подчиняются закону нормального распределения. Непараметрические методы не накладывают ограничений на закон распределения изучаемых величин. Значение линейного коэффициента корреляции важно для исследования социально-экономических явлений и процессов, распределение которых близко к нормальному. Он принимает значения в интервале: -1≤ r ≤ 1. По степени тесноты связи различают количественные критерии оценки тесноты связи. Оценка линейного коэффициента корреляции может быть произведена по таблице 1, либо укрупненно по таблице 2. Таблица 1 Количественные критерии оценки тесноты связи
Таблица 2 Укрупненные критерии оценки тесноты связи
Отрицательные значения указывают на обратную связь, положительные - на прямую. При r = 0 линейная связь отсутствует. Чем ближе коэффициент корреляции по абсолютной величине к единице, тем теснее связь между признаками. И, наконец, при r = ±1 - связь функциональная. По направлению выделяют связь прямую и обратную. При прямой связи с увеличением или уменьшением значений факторного признака происходит увеличение или уменьшение значений результативного. В случае обратной связи значения результативного признака изменяются под воздействием факторного, но в противоположном направлении по сравнению с изменением факторного признака. По аналитическому выражению выделяют связи прямолинейные и криволинейные. Если статистическая связь между явлениями может быть приближенно выражена уравнением прямой линии, то ее называют линейной связью; если же она выражается уравнением какой-либо кривой линии (параболы, гиперболы, показательной и др.), то такую связь называют криволинейной. Графически взаимосвязь двух признаков отображается с помощью поля корреляции. В системе координат по оси абсцисс откладываются значения факторного признака, а на оси ординат - результативного. Каждое пересечение линий, проводимых через эти оси, обозначается точкой. Чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связи. Квадрат линейного коэффициента корреляции r2 называется линейным коэффициентом детерминации. Из определения коэффициента детерминации очевидно, что его числовое значение всегда заключено в пределах от 0 до 1, то есть 0 ≤ r2 ≤ 1. Степень тесноты связи полностью соответствует теоретическому корреляционному отношению, которое является более универсальным показателем тесноты связи по сравнению с линейным коэффициентом корреляции. Факт совпадений и несовпадений значений теоретического корреляционного отношения η и линейного коэффициента корреляции r используется для оценки формы связи. Для оценки значимости коэффициента корреляции r используют t-критерий Стьюдента, который применяется при t-распределении, отличном от нормального. Полученное значение tрасч сравнивают с табличным значением t-критерия (для α = 0,05 и 0,01). Если рассчитанное значение tрасч превосходит табличное значение критерия tтабл, то практически невероятно, что найденное значение обусловлено только случайными колебаниями (то есть отклоняется гипотеза о его случайности). Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, следовательно, фактор х не оказывает влияния на результат у. Величина F-отношения (F-критерий) получается при сопоставлении факторной и остаточной дисперсии в расчете на одну степень свободы. F = Dфакт / Dост. F-критерий проверки для нулевой гипотезы Н0: Dфакт = Dост. Если нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для Н0 необходимо опровержение, чтобы факторная дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором разработаны таблицы критических значений F-отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение F-критерия - это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признается достоверным (отличным от 1), если оно больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: Fфакт > Fтабл Н0 отклоняется. Если же величина оказалась меньше табличной Fфакт < Fтабл, то вероятность нулевой гипотезы меньше заданного уровня (например, 0, 05) и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым и не отклоняется. Проверка адекватности регрессионной модели может быть дополнена корреляционным анализом. Для этого необходимо определить тесноту корреляционной связи между переменными х и у. Теоретическое корреляционное отношение η представляет собой относительную величину, получающуюся в результате сравнения среднего квадратического отклонения выравненных значений результативного признака δ, то есть рассчитанных по уравнению регрессии, со средним квадратическим отношением эмпирических (фактических) значений результативности признака σ. Изменение значения η объясняется влиянием факторного признака. Проверка значимости уравнения регрессии производится на основе дисперсионного анализа. В математической статистике дисперсионный анализ рассмотрен как самостоятельный инструмент (метод) статистического анализа. В эконометрике он применяется как вспомогательное средство для изучения качества модели. Центральное место в анализе дисперсии занимает разложение общей суммы квадратов отклонений переменной у от среднего значения у на две части - «объясненную» и «необъясненную».
9. Интервалы прогноза по линейному уравнению регрессии. Проверка значимости оценок параметров регрессии Интервалы прогноза Оценка статистической значимости параметров регрессии проводится с помощью t-статистики Стьюдента и путем расчета доверительного интервала для каждого из показателей. Выдвигается гипотеза Н0 о статистически значимом отличие показателей от 0 a = b = r = 0. Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что параметры a и b находясь в указанных границах не принимают нулевых значений, т.е. не является статистически незначимыми и существенно отличается от 0. 10 Влияние неучтенных факторов на коэффициент корреляции Далее мы обсудим некоторые важные факторы, которые могут при известных обстоятельствах оказывать влияние на величину коэффициента корреляции, снижая точность его оценки. В конечном итоге это может привести к ошибочным выводам, особенно при сравнении результатов нескольких обследований. Один из таких факторов — географический. Например, при изучении зависимости урожайности от показателей качества почвы необходимо учитывать, производились ли исследования в масштабах округа или района. Коэффициент корреляции, вычисленный по результатам наблюдений в районе, в общем, больше коэффициента корреляции, вычисленного по результатам исследования в округе, так как некоторые факторы при этом либо отсутствуют, либо они не так сильно варьируют. Как правило, при сравнительном анализе могут сопоставляться только такие коэффициенты корреляции, которые относятся к однородным единицам обследования, например к округам или районам. С осторожностью нужно подходить и к обобщению результатов обследования, выполненного в рамках небольшой области. Не всегда правомерно распространять вывод на более крупные территориальные единицы. Например, коэффициент корреляции между доходом и расходами на определенные потребительские товары в расчете на душу населения будет сильно варьировать остеографического признака. Величина коэффициента корреляции зависит также от фактора времени. Так, при изучении связи между прибылью и себестоимостью следует учитывать, за какой период вычисляется по экономическим показателям коэффициент корреляции — за месяц, квартал или год. Коэффициент корреляции только тогда является достоверным показателем связи, когда исследуемые единицы однородны в отношении этой связи. Одно из условий однородности — близость значений количественного признака. Так, при изучении зависимости себестоимости от объема продукции сначала необходимо произвести группировку предприятий, например на крупные, средние и мелкие, а затем по группам вычислять коэффициенты корреляции. В связи с этим возникают задачи формирования однородных многомерных комплексов. Исследователь должен располагать теоретически обоснованным критерием определения статистической однородности, чтобы отбрасывать или относить к другой группе те значения, которые не типичны для данной связи. Построение критерия группировки социально-экономических явлений по комплексу признаков — дело достаточно сложное. Далее мы покажем, что из факта линейной корреляционной связи между абсолютными величинами, по которым вычислены относительные показатели, вовсе не вытекает с необходимостью корреляционная связь между этими относительными показателями. В таких случаях часто возникает нонсенс-корреляция, или псевдокорреляция (ложная корреляция). Особенно сильное влияние на величину коэффициента корреляции оказывает неоднородность исходного материала, например производственные предприятия, на которых производится исследование связи между производительностью труда и уровнем механизации работ, могут очень сильно различаться между собой. При одном и том же уровне механизации работ одно предприятие может быть оснащено современным оборудованием, а другое — устаревшим. Благодаря этому обстоятельству отдельные значения экономических показателей могут более или менее сильно рассеиваться. Связь между явлениями, в общем, интенсивнее, если исследования производятся на большом числе предприятий. Выводы, основанные на большом числе наблюдений, значительно достовернее. Чем меньше объем наблюдений, тем сильнее подвержена колебаниям интенсивность связи от исследования к исследованию. Иногда коэффициенты корреляции, вычисленные по различным частям одной и той же совокупности, различаются даже по своему знаку. В [72] приведены рекомендации по вычислению коэффициента корреляции, свободного от случайных воздействий. |