Выбор формы уравнения регрессии

• Название: Выбор формы уравнения регрессии
• Анкор: kira_shpory.doc
• Дата: 07.05.2018
• Размер: 8.7 Mb.
• Имя файла: kira_shpory.doc
• Тип: Документы; #19000
• страница: 2 из 13

5. Метод наименьших квадратов (МНК). Обобщенный МНК

Метод наименьших квадратов — один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки.

Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.

Задача метода наименьших квадратов состоит в выборе вектора , минимизирующего ошибку . Эта ошибка есть расстояние от вектора до вектора .

Аппроксимация данных и регрессионный анализ

Пусть имеется n значений некоторой переменной y (это могут быть результаты наблюдений, экспериментов и т. д.) и соответствующих переменных x. Задача заключается в том, чтобы взаимосвязь между y и x аппроксимировать некоторой функцией f(x,b), известной с точностью до некоторых неизвестных параметров b, то есть фактически найти наилучшие значения параметров b, максимально приближающие значения к фактическим значениям y. Фактически это сводится к случаю «решения» переопределенной системы уравнений относительно b:



В регрессионном анализе и в частности в эконометрике используются вероятностные модели зависимости между переменными



где e_t — так называемые случайные ошибки модели.

Соответственно, отклонения наблюдаемых значений y от модельных f(x,b) предполагается уже в самой модели. Сущность МНК (обычного, классического) заключается в том, чтобы найти такие параметры b, при которых сумма квадратов отклонений (ошибок, для регрессионных моделей их часто называют остатками регрессии) e_t будет минимальной:



где RRS— англ. Residual Sum of Squares[3] определяется как:



В общем случае решение этой задачи может осуществляться численными методами оптимизации (минимизации). В этом случае говорят о нелинейном МНК (NLS или NLLS — англ. Non-Linear Least Squares). Во многих случаях можно получить аналитическое решение. Для решения задачи минимизации необходимо найти стационарные точки функции RRS(b), продифференцировав её по неизвестным параметрам b, приравняв производные к нулю и решив полученную систему уравнений: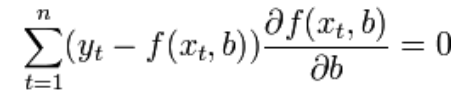



Сущность обобщённого МНК

Известно, что симметрическую положительно определенную матрицу можно разложить как , где P- некоторая невырожденная квадратная матрица. Тогда обобщённая сумма квадратов может быть представлена как сумма квадратов преобразованных (с помощью P) остатков . Для линейной регрессии это означает, что минимизируется величина:

где , то есть фактически суть обобщённого МНК сводится к линейному преобразованию данных и применению к этим данным обычного МНК. Если в качестве весовой матрицы W используется обратная ковариационная матрица V случайных ошибок e (то есть ), преобразование P приводит к тому, что преобразованная модель удовлетворяет классическим предположениям (Гаусса-Маркова), следовательно оценки параметров с помощью обычного МНК будут наиболее эффективными в классе линейных несмещенных оценок. А поскольку параметры исходной и преобразованной модели одинаковы, то отсюда следует утверждение — оценки ОМНК являются наиболее эффективными в классе линейных несмещенных оценок (теорема Айткена). Формула обобщённого МНК имеет вид:



Ковариационная матрица этих оценок равна:

6. Свойства оценок МНК. Проверка качества уравнения регрессии.

Качество модели регрессии связывают с адекватностью модели наблюдаемым (эмпирическим) данным. Проверка адекватности (или соответствия) модели регрессии наблю­даемым данным проводится на основе анализа остатков - .

Анализ остатков позволяет получить представление, насколько хорошо подобрана сама модель и насколько правильно выбран метод оценки коэффициентов. Согласно общим предположениям регрессионного анализа, остатки должны вести себя как независимые (в действительности, почти независимые) одинаково распределенные случайные величины.

Качество модели регрессии оценивается по следующим направлениям:

проверка качества всего уравнения регрессии;

проверка значимости всего уравнения регрессии;

проверка статистической значимости коэффициентов уравнения регрессии;

проверка выполнения предпосылок МНК.

При анализе качества модели регрессии, в первую очередь, используется коэффициент детерминации, который определяется следующим образом: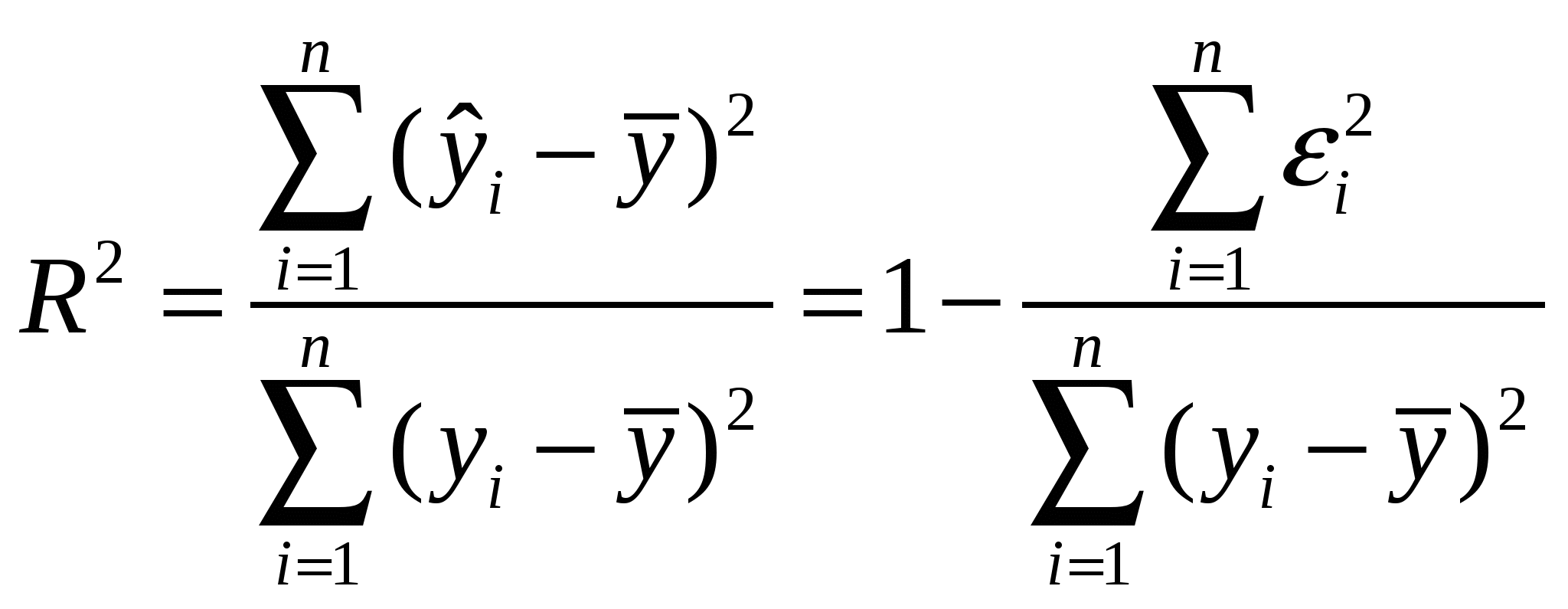

, (2.5)

где - среднее значение зависимой переменной,

- предсказанное (расчетное) значение зависимой переменной.

Коэффициент детерминациипоказывает долю вариации результативного признака, находя­щегося под воздействием изучаемых факторов, т. е. определяет, ка­кая доля вариации признака Y учтена в модели и обусловлена влия­нием на него факторов.

Чем ближе к 1, тем выше качество модели.

Для оценки качества регрессионных моделей целесообразно также ис­пользовать коэффициент множественной корреляции (индекс корреляции) R

R = 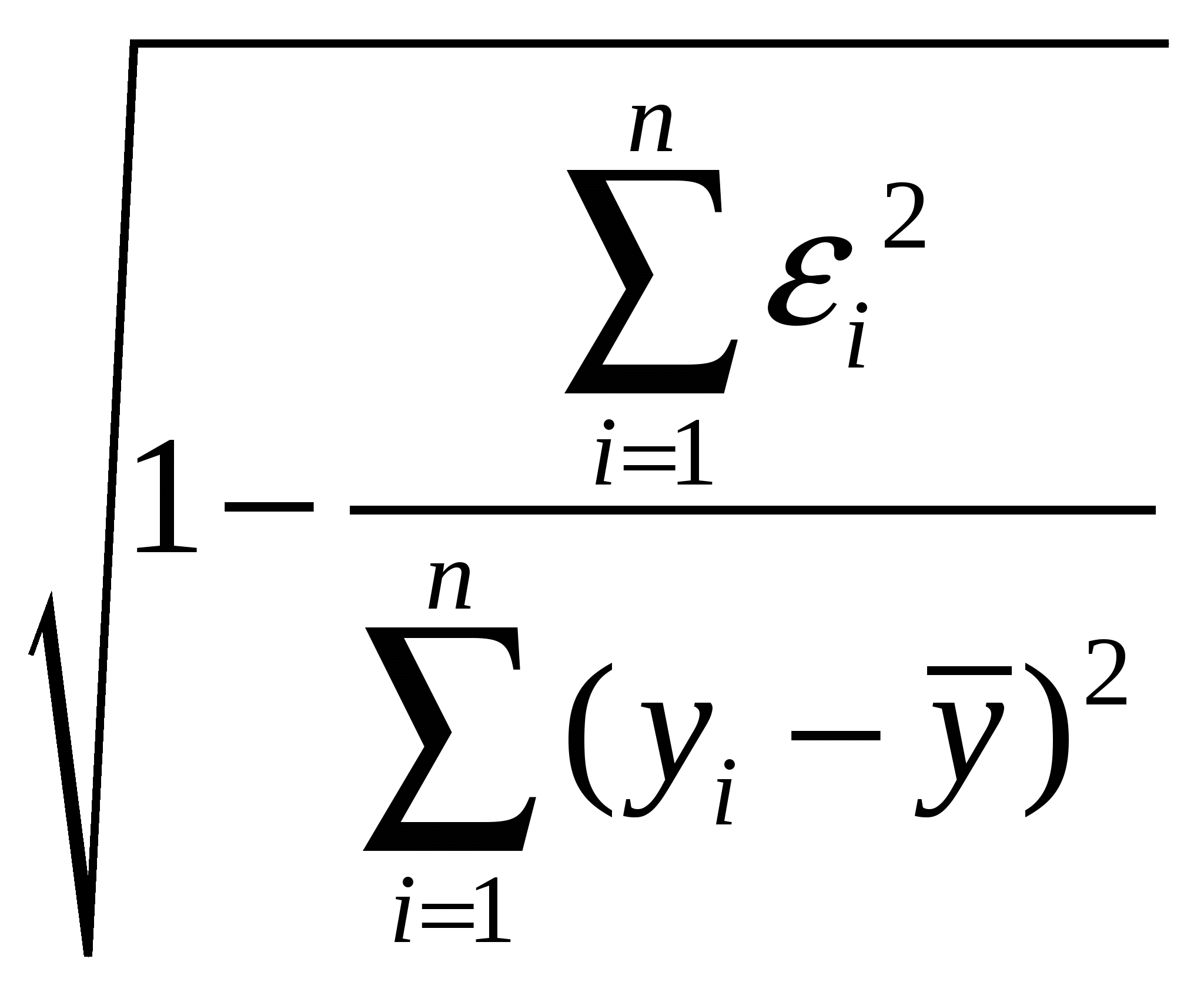= 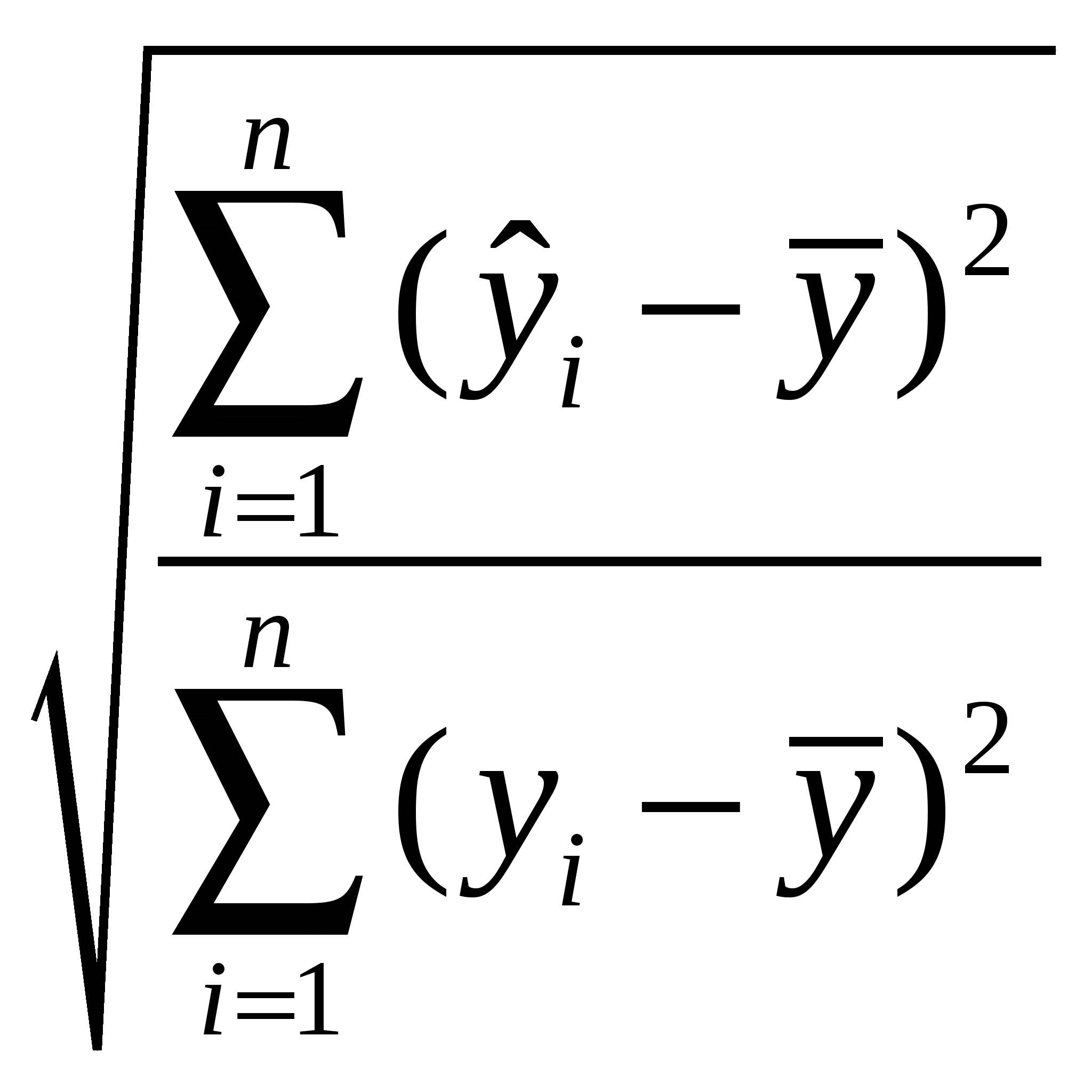(2.6)

Данный коэффициент является универсальным, так как он отра­жает тесноту связи и точность модели, а также может использовать­ся при любой форме связи переменных.

Важным моментом является проверка значимости построенного уравнения в целом и отдельных параметров.

Оценить значимость уравнения регрессии – это означает установить, соответствует ли математическая модель, выражающая зависимость между Y и Х, фактическим данным и достаточно ли включенных в уравнение объясняющих переменных Х для описания зависимой переменной Y

Оценка значимости уравнения регрессии производится для того, чтобы узнать, пригодно уравнение регрессии для практического использования (например, для прогноза) или нет.

Для проверки значимости модели регрессии используется F-критерий Фишера. Если расчетное значение с ₁= k и ₂ = (n - k - 1) степенями свободы, где k – количество факторов, включенных в модель, больше табличного при заданном уровне значимости, то модель считается значимой.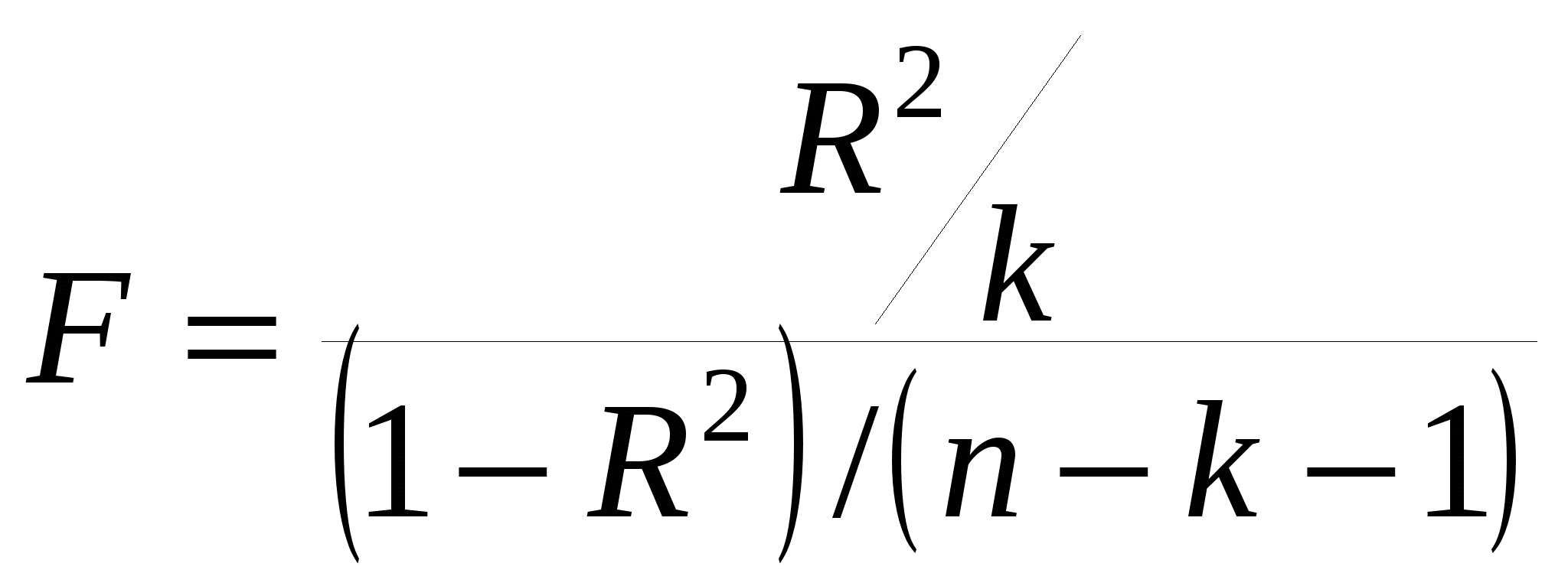

(2.7)

В качестве меры точности применяют несмещенную оценку дис­персии остаточной компоненты, которая представляет собой отно­шение суммы квадратов уровней остаточной компоненты к величи­не (n- k -1), где k – количество факторов, включенных в модель. Квадратный корень из этой величины (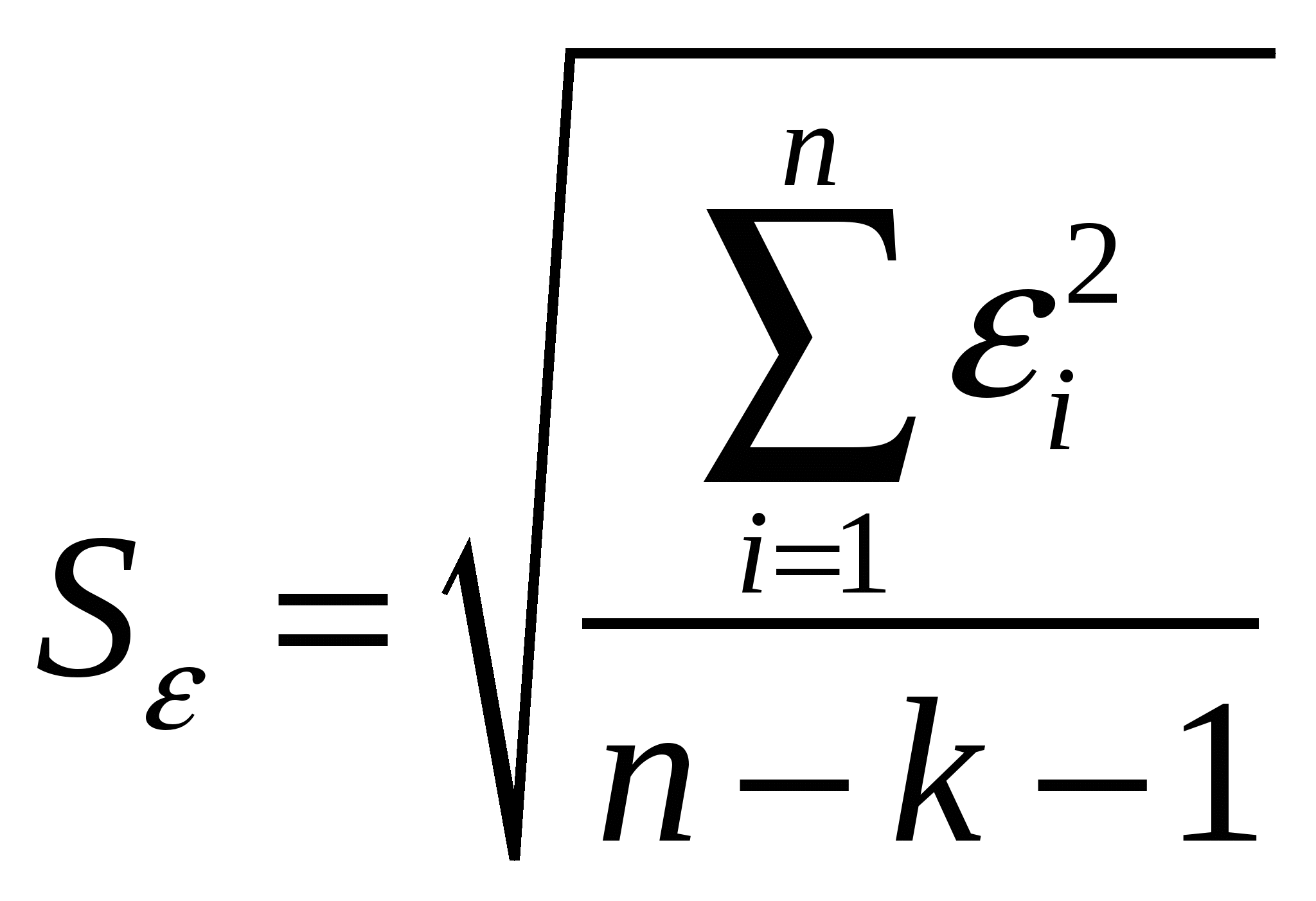) называется стандартной ошибкой:

(2.8)

значимость отдельных коэффициентов регрессии проверяется по t-статистике пу­тем проверки гипотезы о равенстве нулю j-го параметра уравнения (кроме свободного члена):

, (2.9)

где S_aj— это стандартное (среднеквадратическое) отклонение коэффициента уравнения регрессии a_j.Величина S_aj представляет собой квадратный корень из произ­ведения несмещенной оценки дисперсии и j -го диагонального эле­мента матрицы, обратной матрице системы нормальных уравнений.



где - диагональный элемент матрицы .

Если расчетное значение t-критерия с (n - k - 1) степенями сво­боды превосходит его табличное значение при заданном уровне зна­чимости, коэффициент регрессии считается значимым. В противном случае фактор, соответствующий этому коэффициенту, следует ис­ключить из модели (при этом ее качество не ухудшится).

1) математическое ожидание

Теорема: М(а) = , M(b) =  - несмещенность оценок

Это означает, что при увеличении количества наблюдений значения МНК-оценок a и b будут приближаться к истинным значениям  и ;

2) дисперсия

Теорема: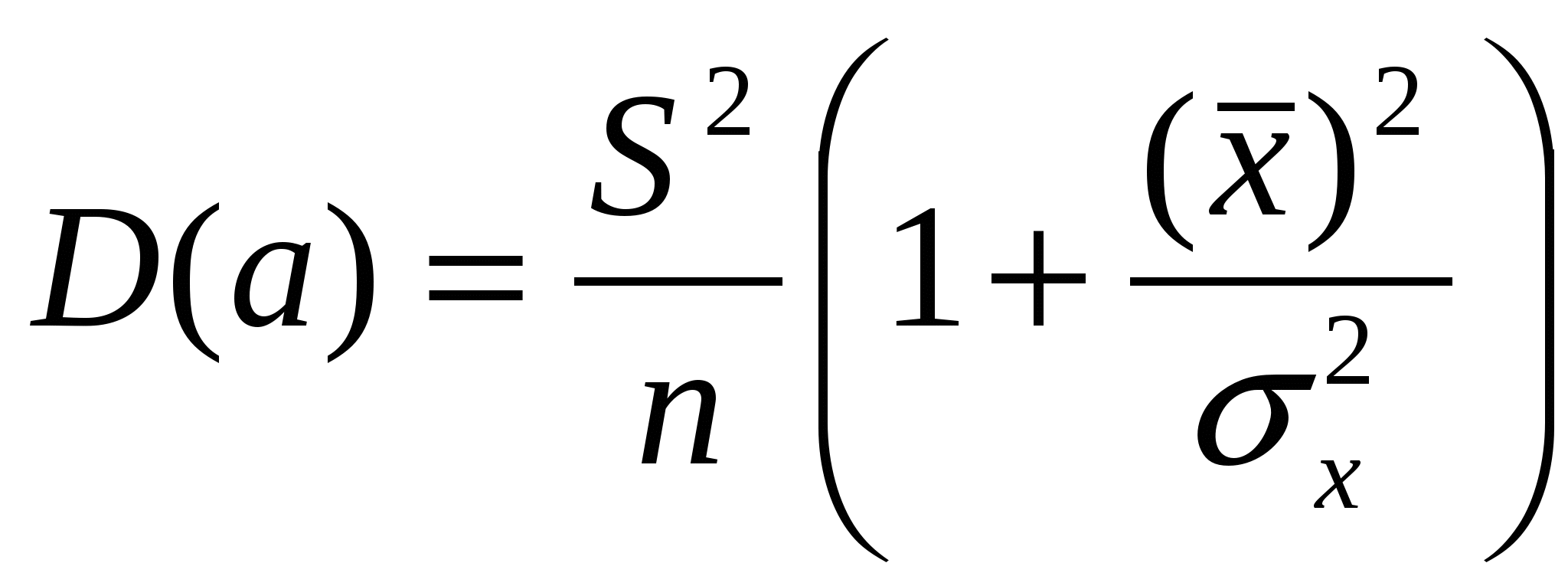

;

Благодаря этой теореме, мы можем получить представление о том, как далеко, в среднем, наши оценки a и b находятся от истинных значений  и .

Необходимо иметь в виду, что дисперсии характеризуют не отклонения, а «отклонения в квадрате». Чтобы перейти к сопоставимым значениям, рассчитаем стандартные отклонения a и b: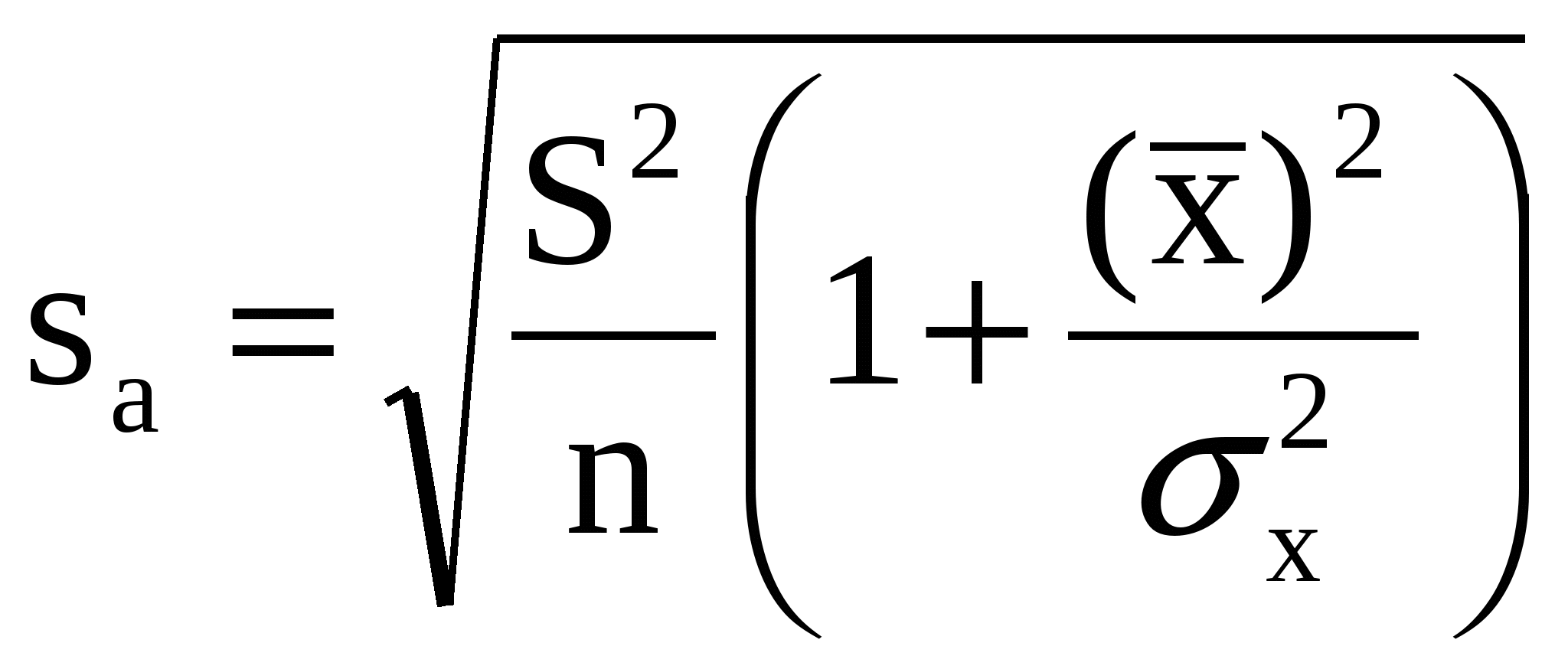

;

Будем называть эти величины стандартными ошибками a и b соответственно.

5. Построение доверительных интервалов

Пусть мы имеем оценку а. Реальное значение коэффициента уравнения регрессии  лежит где-то рядом, но где точно, мы узнать не можем. Однако, мы можем построить интервал, в который это реальное значение попадет с некоторой вероятностью. Доказано, что:



с вероятностью Р = 1 - 

где t_/2(n-1) - /2-процентная точка распределения Стьюдента с (n-1) степенями свободы – определяется из специальных таблиц.

При этом уровень значимости устанавливается произвольно.

Неравенство можно преобразовать следующим образом:





,

или, что то же самое: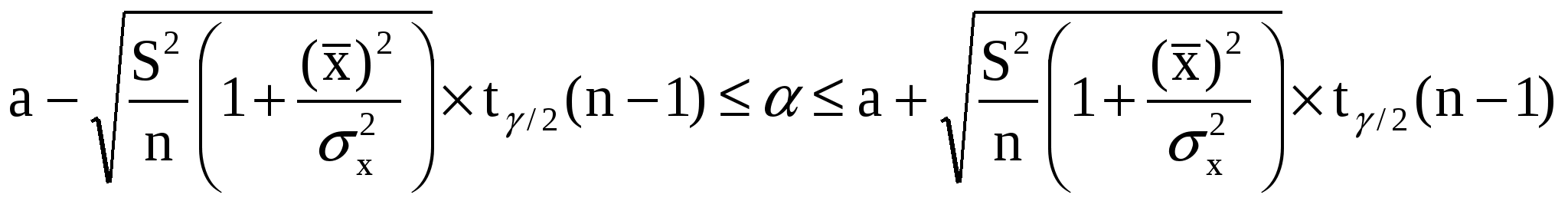



Аналогично, с вероятностью Р = 1 - :



откуда следует:

,

или: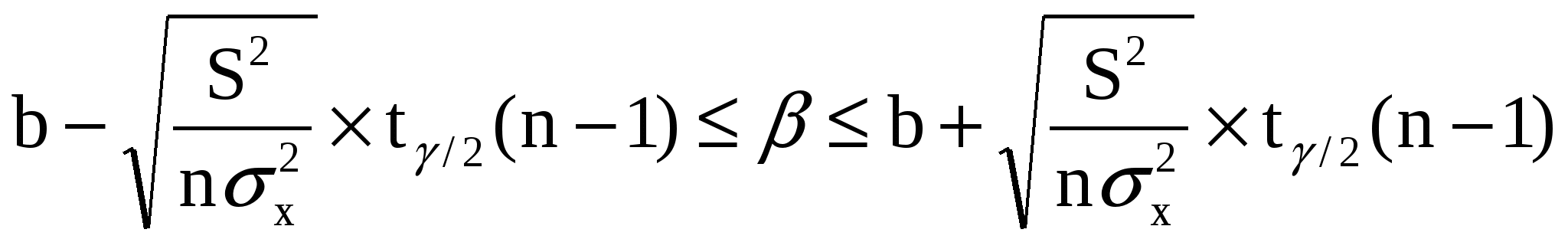



Уровень значимости  - это вероятность того, что на самом деле истинные значения  и  лежат за пределами построенных доверительных интервалов. Чем меньше его значение, тем больше величина t_/2(n-1), соответственно, тем шире будет доверительный интервал.

6. Проверка статистической значимости коэффициентов регрессии

Мы получили МНК-оценки коэффициентов, рассчитали для них доверительные интервалы. Однако мы не можем судить, не слишком ли широки эти интервалы, можно ли вообще говорить о значимости коэффициентов регрессии.

Гипотеза Н₀: предположим, что =0, т. е. на самом деле независимой постоянной составляющей в отклике нет (альтернатива – гипотеза Н₁:   0).

Для проверки этой гипотезы, с заданным уровнем значимости , рассчитывается t-статистика, для парной регрессии:



Значение t-статистики сравнивается с табличным значением t_/2(n-1) - /2-процентной точка распределения Стьюдента с (n-1) степенями свободы.

Если t < t_/2(n-1) – гипотеза Н₀ не отвергается (обратить внимание: не «верна», а «не отвергается»), т. е. мы считаем, что с вероятностью 1- можно утверждать, что  = 0.

В противном случае гипотеза Н₀ отвергается, принимается гипотеза Н₁.

Аналогично для коэффициента b формулируем гипотезу Н₀:  = 0, т. е. переменная, выбранная нами в качестве фактора, на самом деле никакого влияния на отклик не оказывае.

Для проверки этой гипотезы, с заданным уровнем значимости , рассчитывается t-статистика:



и сравнивается с табличным значением t_/2(n-1).

Если t < t_/2(n-1) – гипотеза Н₀ не отвергается, т. е. мы считаем, что с вероятностью 1- можно утверждать, что  = 0.

В противном случае гипотеза Н₀ отвергается, принимается гипотеза Н₁.

7. Автокорреляция остатков.

1. Примеры автокорреляции.

Возможные причины:

1) неверно выбрана функция регрессии;

2) имеется неучтенная объясняющая переменная (переменные)

2. Статистика Дарбина-Уотсона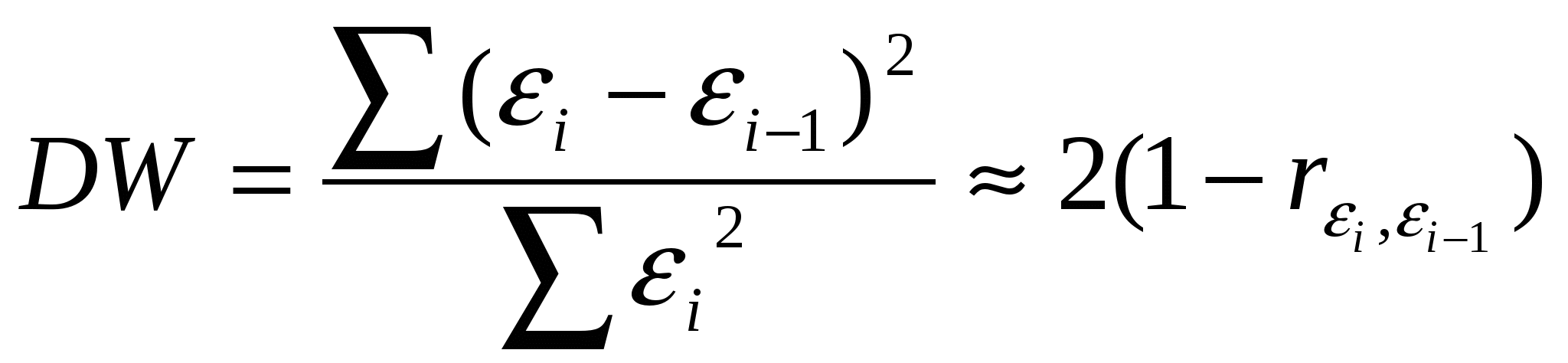



Очевидно:

0  DW  4

Если DW близко к нулю, это позволяет предполагать наличие положительной автокорреляции, если близко к 4 – отрицательной.

Распределение DW зависит от наблюденных значений, поэтому получить однозначный критерий, при выполнении которого DW считается «хорошим», а при невыполнении - «плохим», нельзя. Однако, для различных величин n и  найдены верхние и нижние границы, DW_L и DW_U, которые в ряде случаев позволяют с уверенностью судить о наличии (отсутствии) автокорреляции в модели. Правило:

1) При DW < 2:

а) если DW < DW_L – делаем вывод о наличии положительной автокорреляции (с вероятностью 1-);

б) если DW > DW_U – делаем вывод об отсутствии автокорреляции (с вероятностью 1-);

в) если DW_L  DW  DW_U – нельзя сделать никакого вывода;

2) При DW > 2:

а) если (4 – DW) < DW_L – делаем вывод о наличии отрицательной автокорреляции (с вероятностью 1-);

б) если (4 – DW) > DW_U – делаем вывод об отсутствии автокорреляции (с вероятностью 1-);

в) если DW_L  (4 – DW)  DW_U – нельзя сделать никакого вывода;

8. Гетероскедастичность остатков.

Возможные причины:

- ошибки в исходных данных;

- наличие закономерностей;

Обнаружение – возможны различные тесты. Наиболее простой:

(упрощенный тест Голдфелда – Куандта)

1) упорядочиваем выборку по возрастанию одной из объясняющих переменных;

2) формулируем гипотезу Н₀: остатки гомоскедастичны

3) делим выборку приблизительно на три части, выделяя k остатков, соответствующих «маленьким» х и k остатков, соответствующих «большим» х (kn/3);

4) строим модели парной линейной регрессии отдельно для «меньшей» и «большей» частей

5) оцениваем дисперсии остатков в «меньшей» (s²₁) и «большей» (s²₁) частях;

6) рассчитываем дисперсионное соотношение:



7) определяем табличное значение F-статистики Фишера с (k–m–1) степенями свободы числителя и (k - m - 1) степенями свободы знаменателя при заданном уровне значимости 

8) если дисперсионное соотношение не превышает табличное значение F-статистики (т. е., оно подчиняется F-распределению Фишера с (k–m–1) степенями свободы числителя и (k - m - 1) степенями свободы знаменателя), то гипотеза Н₀ не отвергается - делаем вывод о гомоскедастичности остатков. Иначе – предполагаем их гетероскедатичность.

Метод устранения: взвешенный МНК.

Идея: если значения х оказывают какое-то воздействие на величину остатков, то можно ввести в модель некие «весовые коэффициенты», чтобы свести это влияние к нулю.

Например, если предположить, что величина остатка _i пропорциональна значению x_i (т. е., дисперсия остатков пропорциональна x_i²), то можно перестроить модель следующим образом:



т. е. перейдем к модели наблюдений



где



Таким образом, задача оценки параметров уравнения регрессии методом наименьших квадратов сводится к минимизации функции: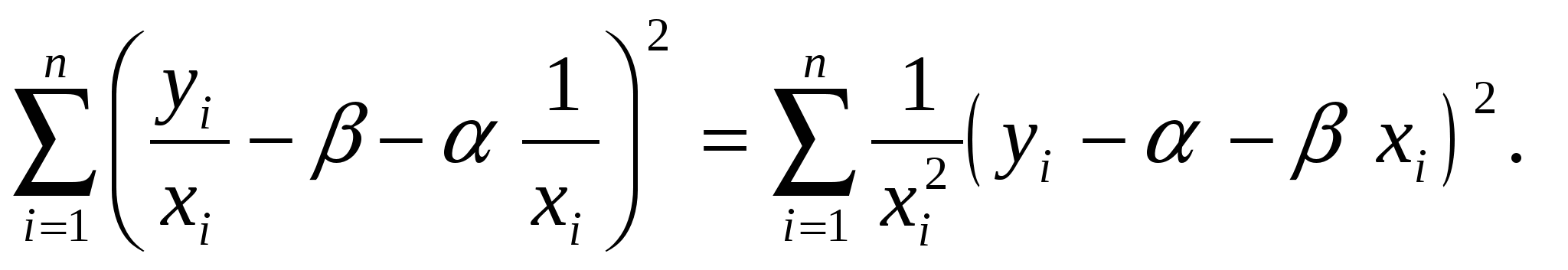



или



где - весовой коэффициент.