Курсова. Вычисление определителя и проверка свойств определителя
 Скачать 0.95 Mb. Скачать 0.95 Mb.
|
СПЕЦИАЛЬНОСТЬ 09.02.03 Программирование в компьютерных системах ПОЯСНИТЕЛЬНАЯ ЗАПИСКА к курсовому проекту на тему: ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЯ И ПРОВЕРКА СВОЙСТВ ОПРЕДЕЛИТЕЛЯ
Москва 2016 Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Московский государственный технический университет имени Н.Э. Баумана» Московский техникум космического приборостроения (МТКП МГТУ им. Н.Э. Баумана) УТВЕРЖДАЮ Председатель ПЦК специальности 09.02.03 Н.А. Жилкина «_____»______________2016 г. ЗАДАНИЕ на выполнение курсового проекта По дисциплине МДК.03.01 Технология разработки программного обеспечения_________ Студент _____________________ Д.В.Эртуганов ТМП-62______________________________ (фамилия, инициалы индекс группы) Руководитель ______________________П.В.Русанов________________ __________ (фамилия, инициалы) График выполнения работы: 25% к 3 нед., 50% к 4 нед., 75% к 5 нед., 100% к 9 нед. 1. Тема курсового проекта Разработка программы вычисления определителя квадратной матрицы (2-го или 3-го порядка) и проверка свойств определителя. 2. Техническое задание определитель не меняется при транспонировании матрицы; если строка или столбец матрицы состоит из нулей, то определитель = 0; от перестановки 2 строк или столбцов определитель меняет знак; определитель матрицы, содержащей 2 одинаковые строки или столбца равен 0; общий множитель всех элементов некоторой строки или столбца можно вынести за знак множителя; определитель матрицы, содержащей 2 пропорциональные строки равен 0; определитель матрицы не изменится, если к элементам одной строки или столбцу прибавить соответственные элементы другой строки или столбца, умноженные на одно и то же число. 3. Оформление курсового проекта 3.1. Пояснительная записка на _______ листах формата А4. 3.2. Перечень графического материала КП (плакаты, схемы, чертежи и т.п.) – схемы алгоритма программы Дата выдачи задания «_16_» _______января________ 2016 г. Руководитель курсового проекта _________________ П.В. Русанов  СОДЕРЖАНИЕ Введение 3 Постановка задачи 5 Структура и описание программы 6 Схемы алгоритма программы 8 3.1 Схема алгоритма основной программы 8 3.2 Схема алгоритма процедуры vvod 15 3.3 Схема алгоритма процедуры vivod 16 3.4 Схема алгоритма процедуры trap 17 3.5 Схема алгоритма функции opr 18 Отладка программы 19 Оптимизация программы 20 Тестирование программы 21 Тестирование в нормальных условиях 21 Тестирование в экстремальных условиях 25 Тестирование в исключительных ситуациях 29 Заключение 31 Список использованных источников 32 Приложение А Листинг программы 33 Приложение Б Результаты выполнения программы 40 Введение Определитель матрицы 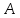 есть число, равное есть число, равное 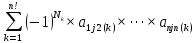 . .Опишем эту формулу словами. Определителем квадратной матрицы порядка n на n является сумма, содержащая 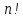 слагаемых. Каждое слагаемое представляет собой произведение n элементов матрицы, причем в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы слагаемых. Каждое слагаемое представляет собой произведение n элементов матрицы, причем в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы 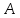 . Перед . Перед 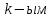 слагаемым появляется коэффициент слагаемым появляется коэффициент 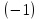 , если элементы матрицы , если элементы матрицы 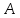 в произведении упорядочены по номеру строки, а количество инверсий в произведении упорядочены по номеру строки, а количество инверсий 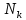 в k-ой перестановке множества номеров столбцов нечетно. в k-ой перестановке множества номеров столбцов нечетно.Определитель матрицы 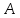 обычно обозначается как обычно обозначается как Итак, 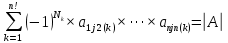 . .Отсюда видно, что определителем матрицы первого порядка является элемент этой матрицы 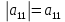 . .Вычисление определителя квадратной матрицы второго порядка - формула и пример.Найдем определитель квадратной матрицы 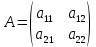 порядка 2 на 2 в общем виде. порядка 2 на 2 в общем виде.В этом случае n=2, следовательно, 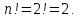 Оформим в виде таблицы необходимые данные для применения формулы. Имеем 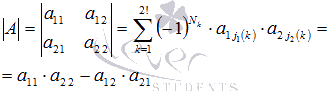 Таким образом, мы получили формулу для вычисления определителя матрицы порядка 2 на 2, она имеет вид 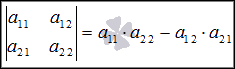 . .Вычисление определителя квадратной матрицы третьего порядка - формула и пример.Найдем определитель квадратной матрицы 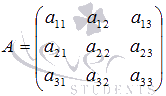 порядка 3 на 3 в общем виде. порядка 3 на 3 в общем виде.В этом случае n=3, следовательно, n!=3!=6. Оформим в виде таблицы необходимые данные для применения формулы 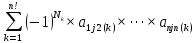 . .Имеем 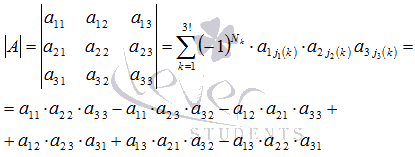 Таким образом, мы получили формулу для вычисления определителя матрицы порядка 3 на 3, она имеет вид 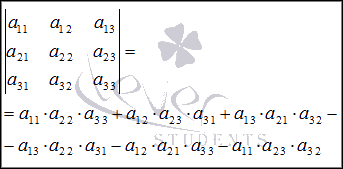 Аналогично можно получить формулы для вычисления определителей матриц порядка 4 на 4, 5 на 5 и более высоких. Они будут иметь очень громоздкий вид. Данный курсовой проект посвящен разработке проверке свойств определителя. Постановка задачи В курсовом проекте требуется написать программу для вычисление определителя квадратной матрицы (2-го или 3-го порядка) и проверки свойств определителя:. определитель не меняется при транспонировании матрицы; если строка или столбец матрицы состоит из нулей, то определитель = 0; от перестановки 2 строк или столбцов определитель меняет знак; определитель матрицы, содержащей 2 одинаковые строки или столбца равен 0; общий множитель всех элементов некоторой строки или столбца можно вынести за знак множителя; определитель матрицы, содержащей 2 пропорциональные строки равен 0; определитель матрицы не изменится, если к элементам одной строки или столбцу прибавить соответственные элементы другой строки или столбца, умноженные на одно и то же число. Разработать программу квадратной матрицы на языке Pascal, IBM PC с объемом ОЗУ не менее 128мб. Структура и описание программы Структура программы приведена на рисунке 2.1  Рисунок 2.1 — Структура программы Подпрограммы, используемые в основной программе, приведены в таблице 2.1: Таблица 2.1 – Используемые подпрограммы
Переменные, используемые в основной программе, приведены в таблице 2.2: Таблица 2.2 – Используемые переменные
СХЕМЫ АЛГОРИТМА ПРОГРАММЫ Схема алгоритма основной программы      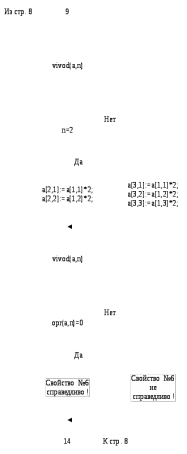  Схема алгоритма процедуры vvod  Схема алгоритма процедуры vivod  Схема алгоритма процедуры trap 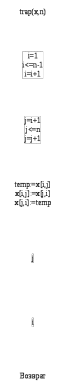 Схема алгоритма функции opr  Отладка программы Отладка – процесс локализации и исправления ошибок в программном коде. Этот процесс занимает значительную часть разработки, нередко - большую, по сравнению с составлением программы. Практически любая программа перед началом отладки содержит ошибки. Во время отладки можно наблюдать следующие ошибки: синтаксические; ошибки компоновки; ошибки выполнения; ошибки логики. Синтаксические ошибки - ошибки, фиксируемые компилятором (транслятором, интерпретатором) при выполнении синтаксического и частично, семантического анализа программы. Заключаются в несовпадении исходного кода с синтаксисом выбранного языка программирования. Ошибки компоновки – ошибки, обнаруженные компоновщиком (редактором связей) при объединении модулей программы. Заключаются в несовпадении каких-либо связей при подключении модулей и подпрограмм или при обращении к ним. Ошибки выполнения – происходят во время вычислений и чаще всего приводят к завершению работы программы. Самый распространенный пример такой ошибки - деление на ноль. Ошибки логики – не позволяют программе выполнять предполагаемые действия. Код может компилироваться и выполняться без ошибок, но результат операции может оказаться неожиданным и неверным. Во время работы были выявлены ошибки: синтаксическая ошибка: отсутствие символа «;» в конце строки; знак «*» вместо «+». логическая ошибка: была забыта установка проверки на вводе размерности матрицы. Все ошибки были исправлены. Для того чтобы убедиться в правильности работы программы, необходимо провести ее тестирование. Оптимизация программы В процессе разработки программы возникла необходимость в оптимизации алгоритма программы. Оптимизация проводилась по времени выполнения программы и по используемой памяти в процессе выполнения. В процессе оптимизации по времени были выполнены следующие шаги: реорганизация циклов таким образом, чтобы снизить количество инициализаций; внутренняя оптимизация циклов, чтобы все повторяющиеся вычисления, не зависящие от параметров цикла, производились снаружи цикла; переменным были присвоены значения при их объявлении, где это было возможно. Оптимизация памяти была выполнена посредством значительного сокращения количества необходимых переменных. Таким образом, удалось снизить время выполнения программы, а также объем выделяемой памяти. Для сокращения времени выполнения программы условный оператор в программе был вынесен за цикл, что позволило сократить количество инициализаций и завершений цикла. 6 ТЕСТИРОВАНИЕ программы Тестирование — набор процедур и действий, предназначенных для демонстрации правильности работы программы в заданных режимах и внешних условиях. Цель тестирования - выявить наличие ошибок или продемонстрировать отсутствие ошибок и правильность работы программы. Для того чтобы протестировать составленную программу, есть три способа тестирования, которые и были применены к данной программе: в нормальных условиях; в экстремальных условиях; в исключительных ситуациях. Тестирование в нормальных условиях Для проведения тестирования в нормальных условиях, воспользуемся входными данными, которые лежат внутри диапазона допустимых значений. В данном случае диапазон допустимых значений для элементов матрицы — от -1000 до 1000. Результат ввода элементов в матрицу приведен на рисунке 6.1. 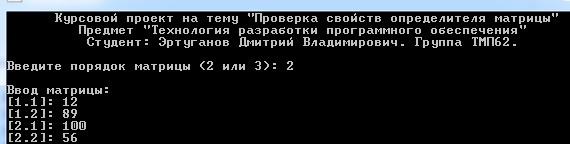 Рисунок 6.1 — Результат ввода элементов в матрицу Вывод МЕНЮ приведен на рисунке 6.2.  Рисунок 6.2 — Вывод МЕНЮ Для проверки работы программы в нормальных условиях протестируем все пункты МЕНЮ. Результат проверки свойства №1 приведен на рисунке 6.3. 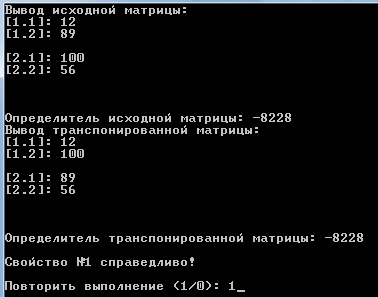 Рисунок 6.3 — Результат проверки свойства №1 Ручной просчет определителя матрицы det A = 12·56 - 100·89 = 672 - 8900 = -8228. Ручной просчет определителя транспонированной матрицы det = 12·56 - 89·100 = 672 - 8900 = -8228. Результат проверки свойства №2 приведен на рисунке 6.4. 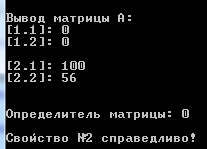 Рисунок 6.4 — Результат проверки свойства №2 Ручной просчет определителя матрицы det A = 0·56 - 100·0 = 0 - 0 = 0 . Результат проверки свойства №3 приведен на рисунке 6.5. 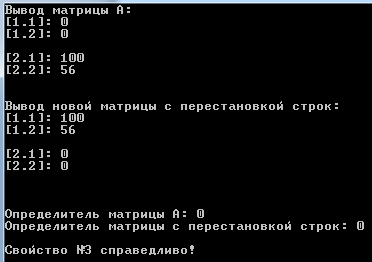 Рисунок 6.5 — Результат проверки свойства №3 Ручной просчет определителя матрицы det A = 0·56 - 100·0 = 0 - 0 = 0 . Ручной просчет определителя новой матрицы det A = 0·100 - 56·0 = 0 - 0 = 0. Результат проверки свойства №4 приведен на рисунке 6.6. 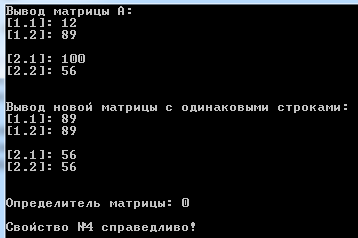 Рисунок 6.6 — Результат проверки свойства №4 Ручной просчет определителя матрицы det A =0·56 - 100·0 = 0 - 0 = 0 . Ручной просчет определителя новой матрицы det A = 89·56 - 56·89 = 4984 - 4984 = 0. Результат проверки свойства №5 приведен на рисунке 6.7. 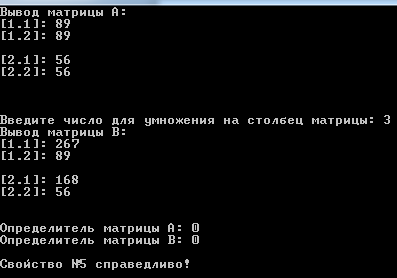 Рисунок 6.7 — Результат проверки свойства №5 Ручной просчет определителя матрицы det A = 89·56 - 56·89 = 4984 - 4984 = 0. Ручной просчет определителя новой матрицы det A = 267·56 - 168·89 = 14952 - 14952 = 0. Результат проверки свойства №6 приведен на рисунке 6.8. 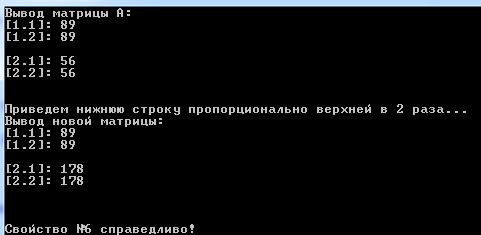 Рисунок 6.8 — Результат проверки свойства №6 det A = 89·178 - 178·89 = 15842 - 15842 = 0. Результат проверки свойства №7 приведен на рисунке 6.9. 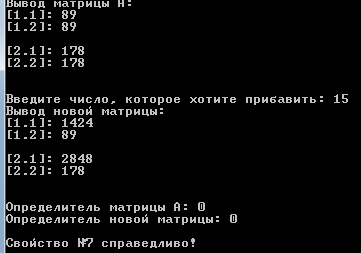 Рисунок 6.9 — Результат проверки свойства №7 Ручной просчет определителя матрицы det A = 89·178 - 178·89 = 15842 - 15842 = 0. Ручной просчет определителя новой матрицы det A =1424·178 - 2848·89 = 253472 - 253472 = 0. Ручной и машинный просчет совпали, следовательно, расчет обратной матрицы с учетом данной нам формулы в нормальных условиях работает верно. Тестирование в экстремальных условиях Экстремальные условия проводятся при значениях для множителей и степеней переменных на границе диапазона допустимых значений — от -1000 до 1000. При увеличении множителей до данных значений, проблем в работе программы не обнаруживается (рисунок 6.10). Результат ввода элементов в матрицу приведен на рисунке 6.10. 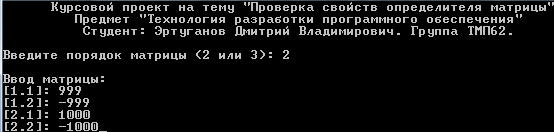 Рисунок 6.10 — Результат ввода элементов в матрицу Результат проверки свойства №1 приведен на рисунке 6.11. 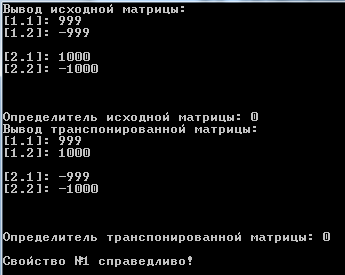 Рисунок 6.11 — Результат проверки свойства №1 Ручной просчет определителя матрицы det A = 999·(-1000) - 1000·(-999) = -999000 + 999000 = 0. Ручной просчет определителя транспонированной матрицы det A = 999·(-1000) - (-999)·1000 = -999000 + 999000 = 0. Результат проверки свойства №2 приведен на рисунке 6.12. 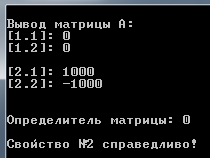 Рисунок 6.12 — Результат проверки свойства №2 Ручной просчет определителя матрицы det A = 0·(-1000) - 1000·0 = 0 - 0 = 0. Результат проверки свойства №3 приведен на рисунке 6.13. 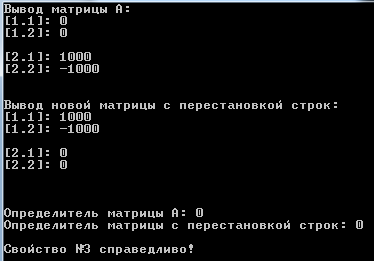 Рисунок 6.13 — Результат проверки свойства №3 Ручной просчет определителя det A = 0·(-1000) - 1000·0 = 0 - 0 = 0. Ручной просчет определителя новой матрицы det A = 1000·0 - 0·(-1000) = 0 + 0 = 0. Результат проверки свойства №4 приведен на рисунке 6.14. 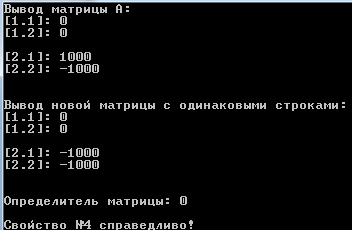 Рисунок 6.14 — Результат проверки свойства №4 Ручной просчет определителя det A = 0·(-1000) - 1000·0 = 0 - 0 = 0. Ручной просчет определителя новой матрицы det A = 0·(-1000) - (-1000)·0 = 0 + 0 = 0. Результат проверки свойства №5 приведен на рисунке 6.15. 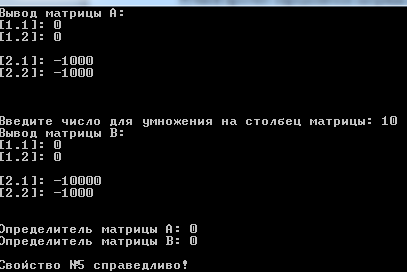 Рисунок 6.15 — Результат проверки свойства №5 Ручной просчет определителя матрицы det A = 0·(-1000) - (-1000)·0 = 0 + 0 = 0. Ручной просчет определителя новой матрицы det A = 0·(-1000) - (-10000)·0 = 0 + 0 = 0. Результат проверки свойства №6 приведен на рисунке 6.16. 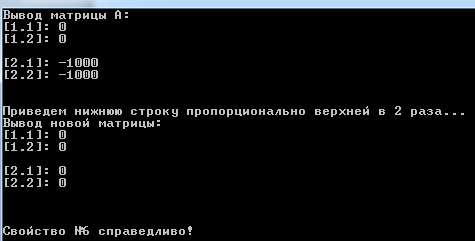 Рисунок 6.16 — Результат проверки свойства №6 Результат проверки свойства №7 приведен на рисунке 6.17. 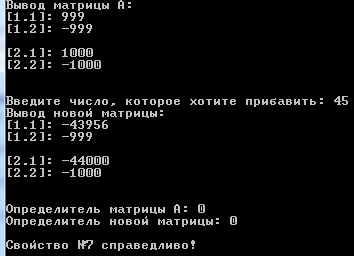 Рисунок 6.17 — Результат проверки свойства №7 Ручной просчет определителя матрицы det A = 999·(-1000) - 1000·(-999) = -999000 + 999000 = 0. Ручной просчет определителя новой det A = (-43956)·(-1000) - (-44000)·(-999) = 43956000 - 43956000 = 0. Ручной и машинный просчет совпали, следовательно, расчет обратной матрицы с учетом данной нам формулы в нормальных условиях работает верно. В итоге, повышение значений матрицы до критических областей не вызывает ошибок в работе программы, но понижает скорость выполнения. Тестирование в исключительных ситуациях Для проверки в исключительных условиях значения множителей будут браться вне области от -1000 до 1000 (рисунок 6.18). 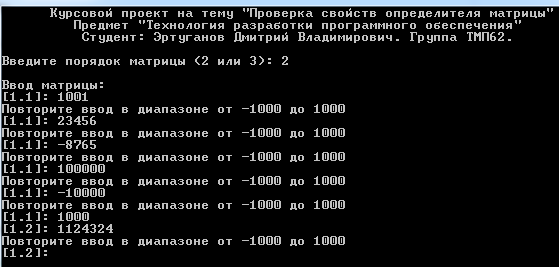 Рисунок 6.18 — Работа программы со значениями, лежащими вне области допустимых значений Тестирование в исключительных условиях показало, что программа отвергает значениями, выходящие за границы области допустимых значений и повторно выводит номер нужной ячейки для повторного ввода. Все этапы тестирования были проведены успешно. Итоги тестирования показали, что изменения в значениях элементов матрицы не влияют на успешность работы программы (но понижают время выполнение), в то время как выход за границы не допускается. Листинг программы приведен в приложении А, а результаты выполнения программы — в приложении Б. ЗАКЛЮЧЕНИЕ По итогам выполнения курсового проекта была получена программа с возможностью вычисления определителя квадратной матрицы (2-го или 3-го порядка) и проверкой свойств определителя. Ее можно использовать в учебных целях. Листинг программы имеет понятные пошаговые комментарии, позволяющие увидеть алгоритм ее работы. Имеется простой и удобный в использовании интерфейс. В процессе разработки были выявлены некоторые недостатки разработанной программы. К ним можно отнести то, что программа подходит лишь для матриц относительно небольшого порядка (2-3). К достоинствам программы можно отнести оптимизацию кода, наличие проверок вводимых данных, скорость выполнения и понятность. Проведенное тестирование позволило исправить все ошибки и приобрести опыт в отладке программ. Также были получены навыки составления документации. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ Беллман Р. Введение в теорию матриц. М.: Мир, 1969; Биркгоф Г., Барти Т. Современная прикладная алгебра. М.: Мир, 1976, 400 стр. с илл.; Боревич З.И. Определители и матрицы. М.: Наука, 1970; Воеводин В.В. Линейная алгебра. М.: Наука, 1980; Гантмахер Ф.Р. Теория матриц – 5-е изда. М.: Физматлит, 2004 – 560стр.; Головизин В.В., Практические занятия по курсу «Алгебра и геометрия» Ч.3: учеб.-метод. Пособие. Ижевск, 2009, 91стр.; Голуб. Дж., Ван Лоун Ч. Матричные вычисления. М.: Мир, 1999, 548стр., с илл.; Ильин В.А., Позняк Э.Г. Линейная алгебра: Учебник для вузов, - 6-е изд., стер. М.: Физматлит, 2004 – 280стр.; Ланкастер П. Теория матриц. М.: Наука, 1973; Меженный А.О., Turbo Pascal. Самоучитель – Вильямс, Диалектика, 2011, 336 стр.; Орлов С.,Цилькер Б., Технологии разработки программного обеспечения. Питер, 2012, 608 стр.; Сачков В.Н., Тараканов В.Е. Комбинаторика неотрицательных матриц. М.: Научное издательство ТВП, 2000. Хорн.Р., Джонсон Ч. Матричный анализ. М.: Наука, 1989, 655 стр.; Шнейдер В.Е. Краткий курс высшей математики. М.: Высшая школа, 1999; Шпак Ю.А., Turbo Pascal 7.0 на примерах. Юниор, 2003, 496 стр.; ПРИЛОЖЕНИЕ А (обязательное) Листинг программы {Курсовой проект. Предмет "Технология разработки программного обеспечения." Тема: "Поверка свойств определителя квадратной матрицы." Язык: Pascal ABC. Студент: Эртуганов Дмитрий Владимирович. Группа ТМП62. Задача: В курсовом проекте требуется написать программу для проверки свойств определителя квадратной матрицы: 1) Определитель не меняется при транспонировании матрицы. 2) Если строка или столбец матрицы состоит из нулей, то определитель = 0. 3) От перестановки 2 строк или столбцов определитель меняет знак. 4) Определитель матрицы, содержащей 2 одинаковые строки или столбца равен 0. 5) Общий множитель всех элементов некоторой строки или столбца можно вынести за знак множителя. 6) Определитель матрицы, содержащей 2 пропорциональные строки равен 0. 7) Определитель матрицы не изменится, если к элементам одной строки или столбцу прибавить соответственные элементы другой строки или столбца, умноженные на одно и то же число. Используемые переменные: i – индекс строки в матрице; j – индекс столбца в матрице; n – размерность матрицы; a – матрица, исходно заполняемая пользователем; a1,b – матрицы, сформированные для проверки свойств определителя; temp_opr,temp_opr1 – аргументы определителей квадратных матриц; m – аргумент для выбора свойства определителя, подлежащего проверке; k,k1 – аргумент для выбора свойства определителя, подлежащего проверке; f – флаг повторного выполнения программы. Используемые подпрограммы: vvod – процедура ввода элементов в исходную матрицу; vivod – процедура вывода выбранной матрицы; trap – процедура транспонирования выбранной матрицы; opr - функция вычисления определителя.} program HARDKOR_KURSACH; uses crt; type mat=array [1..3,1..3] of integer; var a,a1,b:mat; temp_opr,temp_opr1:integer; n,i,j,m,f:byte; k,k1:shortint; procedure vvod(var x:mat; n:byte); var i,j:byte; {Процедура vvod вводит элементы в матрицу заданной размерности. Формальные параметры: x - аргумент вводимой матрицы; n - аргумент размерности вводимой матрицы. Локальные переменные: i – индекс строки в матрице; j – индекс столбца в матрице.} begin for i:=1 to n do begin for j:=1 to n do begin write('[',i,'.',j,']: '); readln(x[i,j]); while (x[i,j]<-1000) or (x[i,j]>1000) do begin writeln('Повторите ввод в диапазоне от -1000 до 1000'); write('[',i,'.',j,']: '); readln(x[i,j]); end; end; end; end; procedure vivod(var x:mat; n:byte); var i,j:byte; {Процедура vivod форматированного вывода матрицы вещественного типа. заданной размерности. Формальные параметры: x - аргумент выводимой матрицы; n - аргумент размерности выводимой матрицы. Локальные переменные: i – индекс строки в матрице; j – индекс столбца в матрице.} begin for i:=1 to n do begin for j:=1 to n do writeln('[',i,'.',j,']: ',x[i,j]); writeln end; writeln; end; procedure trap(var x:mat; n:byte); var temp:integer; i,j:byte; {Процедура transp транспониронирует матрицу вещественного типа. Формальные параметры: x - аргумент транспонируемой матрицы; n - аргумент размерности выводимой матрицы. Локальные переменные: i – индекс строки в матрице; j – индекс столбца в матрице.} begin for i:=1 to n-1 do for j:=i+1 to n do begin temp:=x[i,j]; x[i,j]:=x[j,i]; x[j,i]:=temp; end; end; function opr(var x:mat; n:byte):integer; {Функция opr вычисляет определитель матрицы вещественного типа. Формальные параметры: x - аргумент исходной матрицы; n - аргумент размерности выводимой матрицы.} begin if n=2 then opr:=x[1,1]*x[2,2]-x[1,2]*x[2,1] else opr:=x[1,1]*x[2,2]*x[3,3]+x[1,2]*x[2,3]*x[3,1]+x[1,3]*x[2,1]*x[3,2]-x[1,3]*x[2,2]*x[3,1]-x[1,2]*x[2,1]*x[3,3]-x[1,1]*x[2,3]*x[3,2]; end; begin clrscr; writeln(' Курсовой проект на тему "Проверка свойств определителя матрицы"'); writeln(' Предмет "Технология разработки программного обеспечения"'); writeln(' Студент: Эртуганов Дмитрий Владимирович. Группа ТМП62.'); writeln; repeat write('Введите порядок матрицы (2 или 3): '); readln(n); until (n>1) or (n<4); writeln; writeln('Ввод матрицы:'); vvod(a,n); writeln; repeat clrscr; writeln('Меню:'); writeln('1) Определитель не меняется при транспонировании матрицы;'); writeln('2) Если строка матрицы состоит из нулей, то определитель = 0'); writeln('3) От перестановки двух строк определитель меняет знак'); writeln('4) Определитель матрицы, содержащей две одинаковые строки = 0'); writeln('5) Если в квадратной матрице все элементы какой-либо строки'); writeln(' умножить на некоторое число k, то определитель полученной матрицы'); writeln(' будет = определителю исходной матрицы, умноженному на k.'); writeln('6) Определитель, содержащий две пропорциональные строки = 0;'); writeln('7) Определитель не изменится, если к элементам одной из его строк '); writeln(' прибавить соответственные элементы другой '); writeln(' строки, умноженные на одно и то же число.'); writeln; writeln('ЗАМЕЧАНИЕ.'); writeln('Все свойства остаются справедливыми, если вместо строк взять столбцы.'); writeln; writeln('Проверка свойства под №: '); readln(m); clrscr; case m of 1: begin //Проверка //свойства №1 writeln('Вывод исходной матрицы:'); vivod(a,n); writeln; temp_opr:=opr(a,n); //Вычисление //определителя writeln('Определитель исходной матрицы: ',temp_opr); a1:=a; trap(a1,n); writeln('Вывод транспонированной матрицы:'); vivod(a1,n); writeln; writeln('Определитель транспонированной матрицы: ',opr(a1,n)); writeln; if temp_opr=opr(a1,n) then //Сравнение //определит. writeln('Свойство №1 справедливо!') else writeln('Свойство №1 не справедливо!'); end; 2: begin //Проверка //свойства №2 a[1,1]:=0; //Обнуление a[1,2]:=0; if n=3 then a[1,3]:=0; writeln; writeln('Вывод матрицы A:'); vivod(a,n); temp_opr:=opr(a,n); //Вычисление //определителя writeln('Определитель матрицы: ',temp_opr); writeln; if temp_opr = 0 then writeln('Свойство №2 справедливо!') else writeln('Свойство №2 не справедливо!'); end; 3: begin //Проверка //свойства №3 if n=2 then begin //Перестановка //строк b[1,1]:=a[2,1]; b[1,2]:=a[2,2]; end else begin b[1,1]:=a[3,1]; b[1,2]:=a[3,2];b[1,3]:=a[3,3]; b[2,1]:=a[2,1];b[2,2]:=a[2,2];b[2,3]:=a[2,3]; b[3,1]:=a[1,1];b[3,2]:=a[1,2];b[3,3]:=a[1,3]; end; writeln('Вывод матрицы А:'); vivod(a,n); writeln('Вывод новой матрицы с перестановкой строк:'); vivod(b,n); writeln; temp_opr:=opr(a,n); //Вычисление //определителя temp_opr1:=opr(b,n); writeln('Определитель матрицы А: ',temp_opr); writeln('Определитель матрицы с перестановкой строк: ',temp_opr1); writeln; if temp_opr=(-temp_opr1) then //Сравнение //определит. writeln('Свойство №3 справедливо!') else writeln('Свойство №3 не справедливо!'); end; 4: begin //Проверка //свойства №4 writeln('Вывод матрицы А:'); vivod(a,n); a[1,1]:=a[1,2]; //Дублирование //строк a[2,1]:=a[2,2]; if n=3 then a[3,1]:=a[3,2]; writeln('Вывод новой матрицы с одинаковыми строками:'); vivod(a,n); temp_opr:=opr(a,n); //Вычисление //определителя writeln('Определитель матрицы: ',temp_opr); writeln; if temp_opr=0 then writeln('Свойство №4 справедливо!') else writeln('Свойство №4 не справедливо!'); end; 5: begin //Проверка //свойства №5 writeln('Вывод матрицы А:'); vivod(a,n); writeln; write('Введите число для умножения на столбец матрицы: '); readln(k); if n=2 then begin b[1,1]:=a[1,1]*k; b[2,1]:=a[2,1]*k; b[2,2]:=a[2,2]; b[1,2]:=a[1,2]; end else for i:=1 to n do for j:=2 to n do begin b[i,j]:=a[i,j]; b[1,1]:=a[1,1]*k; b[2,1]:=a[2,1]*k; b[3,1]:=a[3,1]*k; end; writeln('Вывод матрицы B:'); vivod(b,n); temp_opr:=opr(a,n); //Вычисление //определителя temp_opr1:=opr(b,n); writeln('Определитель матрицы А: ',temp_opr); writeln('Определитель матрицы В: ',temp_opr1); writeln; if temp_opr1=temp_opr*k then //Сравнение //определит. writeln('Свойство №5 справедливо!') else writeln('Свойство №5 не справедливо!'); end; 6: begin //Проверка //свойства №6 writeln('Вывод матрицы А:'); vivod(a,n); writeln('Приведем нижнюю строку пропорционально верхней в 2 раза...'); if n=2 then begin a[2,1]:=a[1,1]*2; //Умножение //строк a[2,2]:=a[1,2]*2; end else begin a[3,1]:=a[1,1]*2; a[3,2]:=a[1,2]*2; a[3,3]:=a[1,3]*2; end; writeln('Вывод новой матрицы:'); vivod(a,n); writeln; if opr(a,n)=0 then //Сравнение //определит. writeln('Свойство №6 справедливо!') else writeln('Свойство №6 не справедливо!'); end; 7: begin //Проверка //свойства №7 writeln('Вывод матрицы А:'); vivod(a,n); temp_opr:=opr(a,n); //Вычисление //определителя write('Введите число, которое хотите прибавить: '); readln(k1); if n=2 then begin //Прибавление //элемента др. //строки b[1,1]:=a[1,1]+(k1*a[1,2]); b[2,1]:=a[2,1]+(k1*a[2,2]); b[1,2]:=a[1,2]; b[2,2]:=a[2,2]; end else for i:=1 to n do for j:=2 to n do b[i,j]:=a[i,j]; b[1,1]:=a[1,1]+(k1*a[1,2])+(k1*a[1,3]); b[2,1]:=a[2,1]+(k1*a[2,2])+(k1*a[2,3]); b[3,1]:=a[3,1]+(k1*a[3,2])+(k1*a[3,3]); writeln('Вывод новой матрицы:'); vivod(b,n); temp_opr1:=opr(b,n); //Вычисление //определителя writeln('Определитель матрицы А: ',temp_opr); writeln('Определитель новой матрицы: ',temp_opr1); writeln; if temp_opr1=temp_opr then //Сравнение //определит. writeln('Свойство №7 справедливо!') else writeln('Свойство №7 не справедливо!'); end; end; writeln; write('Повторить выполнение (1/0): '); //Запрос на //повторение readln(f); until (f<>1); readkey; end. ПРИЛОЖЕНИЕ Б (обязательное) Результаты выполнения программы Результат ввода элементов в матрицу приведен на рисунке Б.1.  Рисунок Б.1 — Результат ввода элементов в матрицу Вывод МЕНЮ приведен на рисунке Б.2.  Рисунок Б.2 — Вывод МЕНЮ Результат проверки свойства №1 приведен на рисунке Б.3.  Рисунок Б.3 — Результат проверки свойства №1 Результат проверки свойства №2 приведен на рисунке Б.4.  Рисунок Б.4 — Результат проверки свойства №2 Результат проверки свойства №3 приведен на рисунке Б.5.  Рисунок Б.5 — Результат проверки свойства №3 Результат проверки свойства №4 приведен на рисунке Б.6.  Рисунок Б.6 — Результат проверки свойства №4 Результат проверки свойства №5 приведен на рисунке Б.7.  Рисунок Б.7 — Результат проверки свойства №5 Результат проверки свойства №6 приведен на рисунке Б.8.  Рисунок Б.8 — Результат проверки свойства №6 Результат проверки свойства №7 приведен на рисунке Б.9.  Рисунок Б.9 — Результат проверки свойства №7 |

