Статистика. Вариант 4 (5 заданий). Задача 1 Количество строк и столбцов в матрице а 3 строки, 3 столбца. В матрице в 3 строки, 3 столбца
 Скачать 53.2 Kb. Скачать 53.2 Kb.
|
|
Вариант 4. Задача 1. 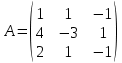 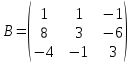 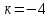 1) Количество строк и столбцов: в матрице А – 3 строки, 3 столбца. В матрице В – 3 строки, 3 столбца. 2) Элемент 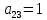 , , 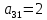 . .3) Сумма элементов главной диагонали матрицы А: 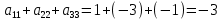 . .4)Произведение элементов побочной диагонали матрицы А: 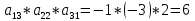 . .5) Транспонированная матрица для матрицы А (поменяем столбцы и строки): 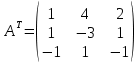 6) 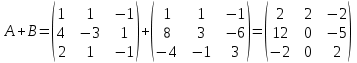 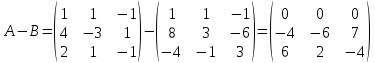 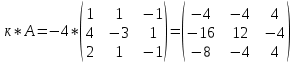 7) Определитель матрицы А: 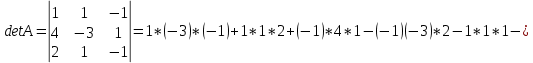 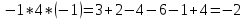 8) Обратная матрица для матрицы А: Запишем матрицу в виде: 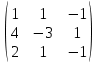 Главный определитель ∆=1∙((-3)∙(-1) - 1∙1) - 4∙(1∙(-1) - 1∙(-1)) + 2∙(1∙1 - (-3)∙(-1)) = -2 Определитель отличен от нуля, следовательно, матрица является невырожденной и для нее можно найти обратную матрицу A-1. Обратная матрица будет иметь следующий вид: 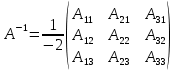 где Aij - алгебраические дополнения. Транспонированная матрица. 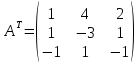 Найдем алгебраические дополнения матрицы AT. 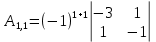 ∆1,1 = ((-3)∙(-1) - 1∙1) = 2 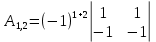 ∆1,2 = -(1∙(-1) - (-1)∙1) = 0 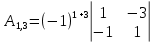 ∆1,3 = (1∙1 - (-1)∙(-3)) = -2 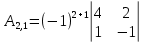 ∆2,1 = -(4∙(-1) - 1∙2) = 6 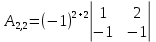 ∆2,2 = (1∙(-1) - (-1)∙2) = 1 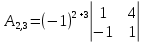 ∆2,3 = -(1∙1 - (-1)∙4) = -5 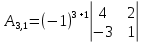 ∆3,1 = (4∙1 - (-3)∙2) = 10 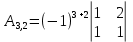 ∆3,2 = -(1∙1 - 1∙2) = 1 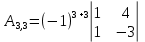 ∆3,3 = (1∙(-3) - 1∙4) = -7 Обратная матрица. 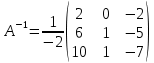 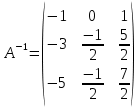 Проверим правильность нахождения обратной матрицы путем умножения исходной матрицы на обратную. Должны получить единичную матрицу E. 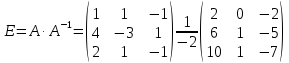 E=A∙A-1=
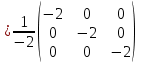 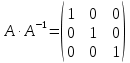 Задача 2. Проверить совместность линейной системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) методом Гаусса; в) методом обратной матрицы. 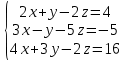 Решение: Исследуем эту систему по теореме Кронекера-Капелли. Выпишем расширенную и основную матрицы: 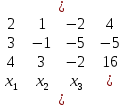 Здесь матрица А выделена жирным шрифтом. Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы. Умножим 1-ую строку на (-3). Умножим 2-ую строку на (2). Добавим 2-ую строку к 1-ой: 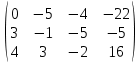 Умножим 2-ую строку на (-4). Умножим 3-ую строку на (3). Добавим 3-ую строку к 2-ой: 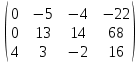 Умножим 1-ую строку на (13). Умножим 2-ую строку на (5). Добавим 2-ую строку к 1-ой: 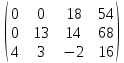 Определим ранг основной системы системы. 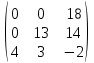 Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля. Ранг этой системы равен rangA=3. Определим ранг расширенной системы системы. 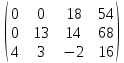 Ранг этой системы равен rangB=3. rang(A) = rang(B) = 3. Поскольку ранг основной матрицы равен рангу расширенной, то система является совместной. а) метод Крамера. Запишем систему в виде: 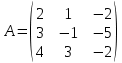 BT = (4,-5,16) Система совместна тогда и только тогда, когда системный (главный) определитель не равен нулю. Определитель: ∆ = 2∙((-1)∙(-2)-3∙(-5))-3∙(1∙(-2)-3∙(-2))+4∙(1∙(-5)-(-1)∙(-2)) = -6 Заменим 1-й столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы. ∆1 = (-1)1+1a11∆11 + (-1)2+1a21∆21 + (-1)3+1a31∆31 = 4∙((-1)∙(-2)-3∙(-5))-(-5)∙(1∙(-2)-3∙(-2))+16∙(1∙(-5)-(-1)∙(-2)) = -24 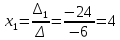 Заменим 2-й столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы. ∆2 = (-1)1+1a11∆11 + (-1)2+1a21∆21 + (-1)3+1a31∆31 = 2∙((-5)∙(-2)-16∙(-5))-3∙(4∙(-2)-16∙(-2))+4∙(4∙(-5)-(-5)∙(-2)) = -12 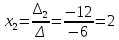 Заменим 3-й столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы. ∆3 = (-1)1+1a11∆11 + (-1)2+1a21∆21 + (-1)3+1a31∆31 = 2∙((-1)∙16-3∙(-5))-3∙(1∙16-3∙4)+4∙(1∙(-5)-(-1)∙4) = -18 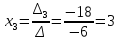 Выпишем отдельно найденные переменные Х 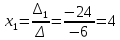 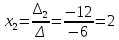 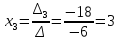 Проверка. 2∙4+1∙2-2∙3 = 4 3∙4-1∙2-5∙3 = -5 4∙4+3∙2-2∙3 = 16 б) метод Гаусса: Запишем систему в виде расширенной матрицы: 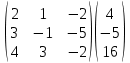 Умножим 1-ю строку на (3). Умножим 2-ю строку на (-2). Добавим 2-ю строку к 1-й: 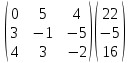 Умножим 2-ю строку на (4). Умножим 3-ю строку на (-3). Добавим 3-ю строку к 2-й: 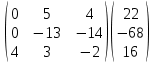 Умножим 1-ю строку на (13). Умножим 2-ю строку на (5). Добавим 2-ю строку к 1-й: 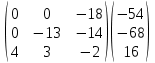 Теперь исходную систему можно записать так: x3 = -54/(-18) x2 = [-68 - ( - 14x3)]/(-13) x1 = [16 - (3x2 - 2x3)]/4 Из 1-й строки выражаем x3 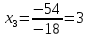 Из 2-й строки выражаем x2 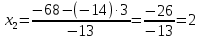 Из 3-й строки выражаем x1 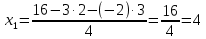 в) Метод обратной матрицы: Итак, определитель -6 ≠ 0, поэтому продолжаем решение. Для этого найдем обратную матрицу через алгебраические дополнения. Пусть имеем невырожденную матрицу А: = Тогда: = где Aij — алгебраическое дополнение элемента aij в определителе матрицы А, которое является произведением (—1)i+j на минор (определитель) n-1 порядка, полученный вычеркиванием i-й строки и j-го столбца в определителе матрицы А. Транспонированная матрица к матрице A имеет вид: Вычисляем алгебраические дополнения. ∆1,1=(-1•(-2)-(-5•3))=17 ∆1,2=-(1•(-2)-(-2•3))=-4 ∆1,3=(1•(-5)-(-2•(-1)))=-7 ∆2,1=-(3•(-2)-(-5•4))=-14 ∆2,2=(2•(-2)-(-2•4))=4 ∆2,3=-(2•(-5)-(-2•3))=4 ∆3,1=(3•3-(-1•4))=13 ∆3,2=-(2•3-1•4)=-2 ∆3,3=(2•(-1)-1•3)=-5 Из полученных алгебраических дополнений составим присоединенную матрицу C: Вычислим обратную матрицу: Вектор результатов X X=A-1 • B XT=(4,2,3) x1=-24 / (-6)=4 x2=-12 / (-6)=2 x3=-18 / (-6)=3 Задача 4. А) 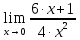 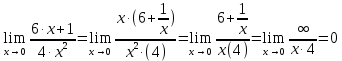 Б) 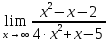 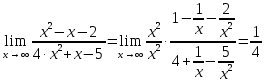 В) 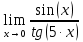 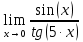 Выполним элементарные преобразования: 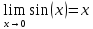 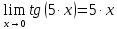 Тогда исходный предел можно представить в виде: 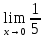 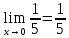 Ответ: 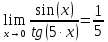 Задача 5. Найти производную в точке 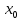 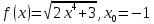 Решение: 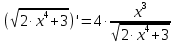 Поскольку: 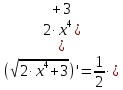 (2∙x4+3)' = 8∙x3 Поскольку: (2∙x4)' = 2∙4∙x4-1(x)' = 8∙x3 (x)' = 1 Получаем: 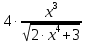 Так как 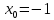 , тогда: , тогда: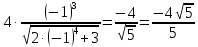 Задача 6. Исследовать функцию по схеме и построить ее график: 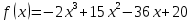 Решение: 1) Область определения функции. X ⊆ R 2) Четность или нечетность функции. 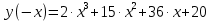 Функция общего вида 3) Точки пересечения кривой с осями координат. Пересечение с осью 0Y 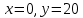 Пересечение с осью 0X y=0 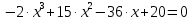 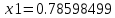 4) Исследование на экстремум. 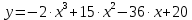 1. Находим интервалы возрастания и убывания. Первая производная. 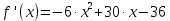 Находим нули функции. Для этого приравниваем производную к нулю 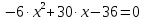 Откуда: 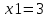 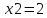
В окрестности точки x = 2 производная функции меняет знак с (-) на (+). Следовательно, точка x = 2 - точка минимума. В окрестности точки x = 3 производная функции меняет знак с (+) на (-). Следовательно, точка x = 3 - точка максимума. 2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная. f''(x) = 30-12∙x Находим корни уравнения. Для этого полученную функцию приравняем к нулю. 30-12∙x = 0 Откуда точки перегиба: x1 = 5/2
5) Асимптоты кривой. y = -2∙x3+15∙x2-36∙x+20 Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты: 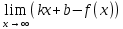 Находим коэффициент k: 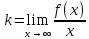 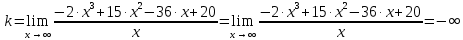 Поскольку коэффициент k равен бесконечности, наклонных асимптот не существует. y = -2∙x3+15∙x2-36∙x+20 Найдем наклонную асимптоту при x → -∞: 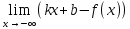 Находим коэффициент k: 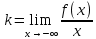 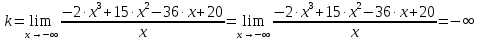 Поскольку коэффициент k равен бесконечности, наклонных асимптот не существует. График функции: 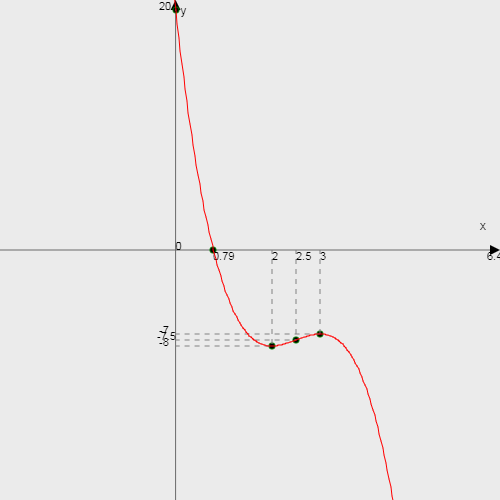 |
