численные методы. ЧМ 1лаб. Вычисление погрешностей результатов арифметических

• Название: Вычисление погрешностей результатов арифметических
• Анкор: численные методы
• Дата: 21.04.2022
• Размер: 3.46 Mb.
• Имя файла: ЧМ 1лаб.docx
• Тип: Лабораторная работа; #489253

Министерство науки и высшего образования Российской Федерации

ФГАОУ ВО «Северо – Восточный федеральный университет им.М.К.Аммосова»

Колледж инфраструктурных технологий

Кафедра эксплуатации и обслуживания информационных систем

Лабораторная работа №1

Тема: ВЫЧИСЛЕНИЕ ПОГРЕШНОСТЕЙ РЕЗУЛЬТАТОВ АРИФМЕТИЧЕСКИХ

ДЕЙСТВИЙ НАД ПРИБЛИЖЁННЫМИ ЧИСЛАМИ.

Выполнил:

ст. гр.ИСИП-20-4 КИТ СВФУ

Заборовский Ю.П.

Проверил(а):

Преподаватель

Петрова А.Г.

Якутск 2022г.

ЛАБОРАТОРНАЯ РАБОТА №1

Цель работы: закрепить знания по пройденной теме; сформировать у студентов знания, умения и навыки работы с приближенными числами в применении формул погрешностей элементарных действий и функций, нахождения значений выражений по способу границ и методом строгого учета абсолютных погрешностей после каждой операции.

Ход работы

Задания:

Задание 1.

1. Что такое абсолютная и относительная погрешности? Раскрыть суть понятия.

Сделать сравнительную характеристику.

Ответ: Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.

Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.

Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.

Получим число 0,0695, переведем в проценты и получим 7 %. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10 % и 0,1 %. Для отрезка длиной в 10 см погрешность в 1 см очень велика, это ошибка в 10 %. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1 %.

2. Как классифицируют виды погрешностей? Перечислить. Раскрыть суть

Ответ: Выделяют следующие виды погрешностей:

1. 
   абсолютная погрешность;
   
2. 
   относительна погрешность;
   
3. 
   приведенная погрешность;
   
4. 
   основная погрешность;
   
5. 
   дополнительная погрешность;
   
6. 
   систематическая погрешность;
   
7. 
   случайная погрешность;
   
8. 
   инструментальная погрешность;
   
9. 
   методическая погрешность;
   
10. 
    личная погрешность;
    
11. 
    статическая погрешность;
    
12. 
    динамическая погрешность.
    

3. Что значит цифра, верная в строгом, широком смыслах? Обосновать

Ответ: Цифра приближенного числа называется верной в широком смысле, если абсолютная (предельная абсолютная) погрешность этого числа не превосходит единицы десятичного разряда, соответствующего этой цифре, в противном случае сомнительной в широком смысле.

4. Как находится погрешность округленного числа? Раскрыть суть

Ответ: Если некоторые исходные данные имеют больше десятичных знаков (при сложении и вычитании) или больше значащих цифр (при других действиях), чем другие, то их предварительно следует округлить, сохраняя лишь одну "запасную цифру".

5. Как определить количество верных цифр по абсолютной погрешности.

Ответ Цифры приближенного числа а называют верными в узком смысле, если абсолютная погрешность приближенного числа а не превосходит половины единицы (т-п+1) – го разряда, которому принадлежит цифра, т.е. если

Задания 2.

2.1. Дано число х=0,00006 и его приближение значение а =0,00005. Найти абсолютную и относительную погрешности числа а.



2.2. Определить значащие цифры числа а.

а = 0,02809 => значащие цифры: ?

а = 0,0280 => значащие цифры: ?

а = 2800 => значащие цифры: ?




2.3.Определить верные цифры приближенного числа а=0,8164, если абсолютная погрешность Δа =0,0021.



2.4. Определить, какое равенство точнее 12/17=0,705 или √51=7,14?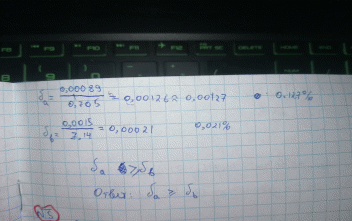





2.5. Округлить сомнительные цифры числа х=45,156 ± 0,016. Определить абсолютную

погрешность результата



2.6.Округлить сомнительные цифры числа а=37,8132 (± 0,0045), оставив верные знаки в узком смысле. Определить абсолютную погрешность результата.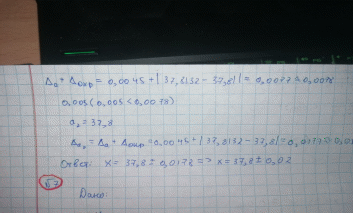





2.7. Округлить сомнительные цифры числа а=15,8312, оставив верные знаки в узком смысле. Определить абсолютную погрешность числа, если δа= 0,3%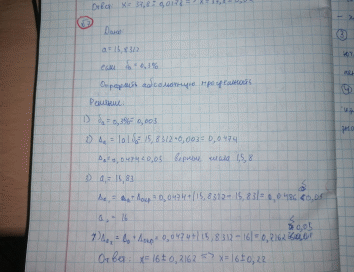



Задания 3.

Контрольные вопросы:

1. Дайте определение понятию погрешности при измерении величин. Раскрыть суть

понятия.



2. Как определяется точность приближенного значения величины? Раскрыть суть



3. Какие цифры называются значащими при измерениях? Дать понятие

4. Что называются абсолютной и относительной погрешностью величин? Приведите

примеры. Сделать сравнительную характеристику