9)Вычисление значений тригонометрических выражений. Вычисление значений тригонометрических выражений Задание. Найдите, если и Решение

• Название: Вычисление значений тригонометрических выражений Задание. Найдите, если и Решение
• Дата: 04.10.2022
• Размер: 0.66 Mb.
• Имя файла: 9)Вычисление значений тригонометрических выражений.docx
• Тип: Решение; #712643

Вычисление значений тригонометрических выражений

Задание. Найдите  , если   и 

Решение.

Поскольку угол альфа лежит в четвёртой четверти, его тангенс отрицателен. Поэтому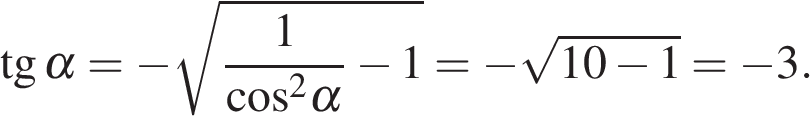



 Ответ: −3.

Задание. Найдите  , если   и 

Решение.

Поскольку угол альфа лежит в третьей четверти, его тангенс положителен. Поэтому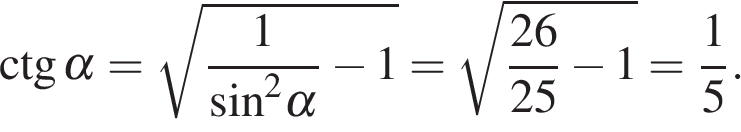



Тогда



 Ответ: 5.

Задание. Найдите 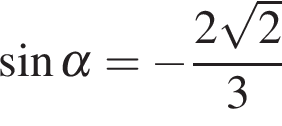 , если   и 

Решение.

Поскольку угол α лежит в четвертой четверти, его косинус положителен. Поэтому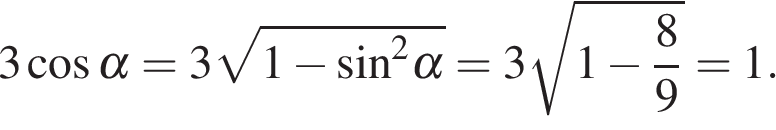



 Ответ: 1.

Задание. Найдите 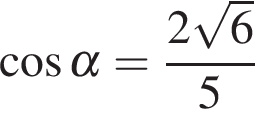 , если   и 

Решение.

Поскольку угол альфа лежит в четвертой четверти, его синус отрицателен. Тогда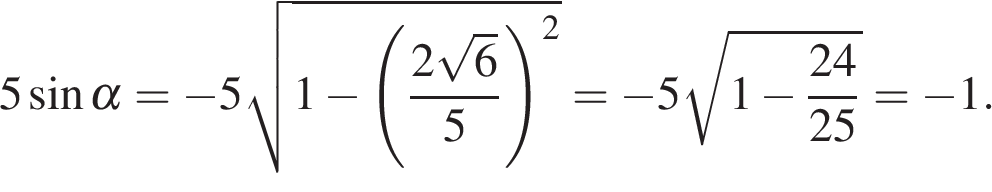



Ответ: −1.

Задание. Найдите  , если 

Решение.

Используем формулу косинуса двойного угла   Имеем:



 Ответ: 22,08.

Задание. Найдите  , если 

Решение.

Выполним преобразования:

 = 

 Ответ: 4.

Задание. Найдите значение выражения  , если 

Решение.

В силу периодичности тангенса   Поэтому



 Ответ: −28.

Задание. Найдите  , если   и 

Решение.

Выполним преобразования:



 Угол   лежит во второй четверти, поэтому   Тогда



 Ответ: 0,6.

Задание. Найдите  , если   и 

Решение.

Поскольку угол 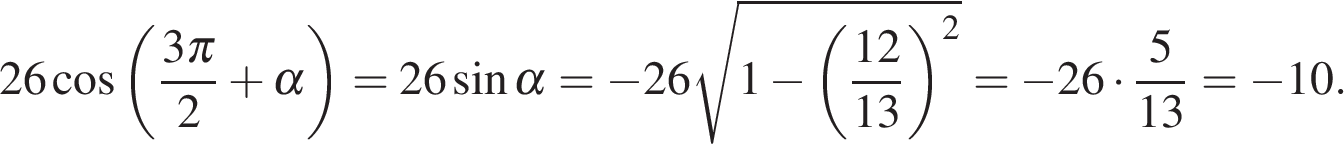  лежит в четвертой четверти,   Применим формулу приведения, а затем выразим синус через косинус. Имеем:



 Ответ: −10.

Задание. Найдите  , если 

Решение.

Пользуемся периодичностью тангенса и используем формулу приведения:



 Ответ: −2,5.

Задание. Найдите  , если 

Решение.

Выполним преобразования: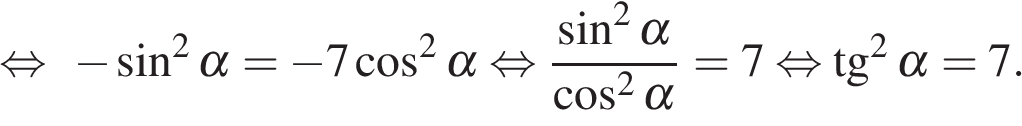





Ответ: 7.

Задание. Найдите  , если 

Решение.

Способ 1:   Тогда:



Способ 2: разделим числитель и знаменатель дроби на   Тогда:



 

Ответ: −9.

Задание. Найдите  , если 

Решение.

Способ 1:   Тогда:



Способ 2: Поделим числитель и знаменатель дроби на  :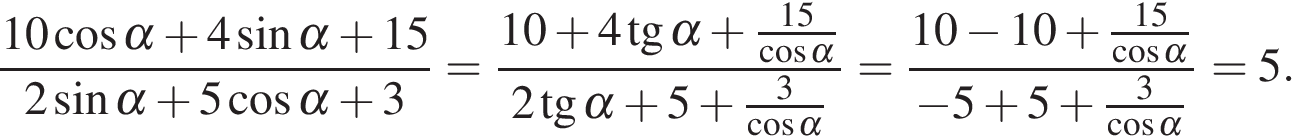



 Ответ: 5.

Задание. Найдите  , если 

Решение.

Разделим числитель и знаменатель на  :



Тогда



 Ответ: 8.

Задание. Найдите  , если 

Решение.

Используем свойство пропорции:

 

Следовательно, 

 Ответ: 2,25.

Задание. Найдите значение выражения

  , если 

Решение.

Используем периодичность косинуса, нечетность синуса и формулы приведения:



 Ответ: 3.

Задание. Найдите значение выражения  , если 

Решение.

В силу нечетности и периодичности синуса

   Далее по формулам приведения имеем:



 Ответ: 4.

Задание. Найдите  , если 

Решение.

Выполним преобразования:



 Ответ: −7.

Задание. Найдите  , если 

Решение.

По формуле   имеем:

 



 Ответ:31,96.

Задание. Найдите значение выражения 

Решение.

Преобразуем выражение и воспользуемся формулой приведения:



Задание. Найдите значение выражения 

Решение.

Последовательно получаем:



 Ответ: 9,5.

Задание. Найдите значение выражения 

Решение.

Заметим, что   поэтому



 Ответ: 14,75.

Задание. Найдите значение выражения 

Решение.

Преобразуем выражение:



 Ответ: 42.

Задание. Найдите значение выражения 

Решение.

Сходственные функции дополнительных углов равны. Поэтому



 Ответ: 46.

Задание. Найдите значение выражения   если

 и 

Решение.

Поскольку угол альфа лежит во второй четверти, его тангенс отрицателен. Поэтому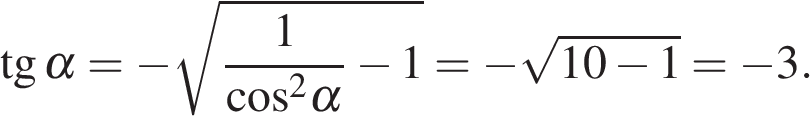



 

Ответ: −3.

Задание. Найдите значение выражения: 

Решение.

Сходственные функции дополнительных углов равны, поэтому



 Ответ: 32.

Задание. Найдите значение выражения 

Решение.

Используем формулу косинуса двойного угла  :



 Ответ: 5.

Задание. Найдите 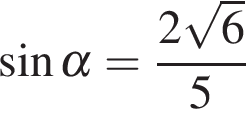  если   и 

Решение.

Поскольку угол 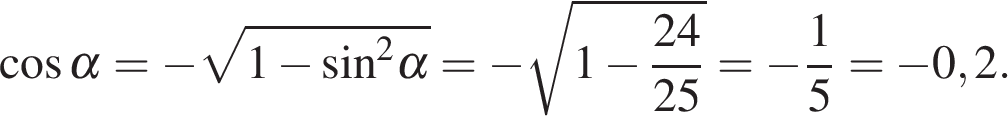  лежит во второй четверти, его косинус отрицателен. Поэтому



 Ответ: −0,2.

Задание. Найдите   если   и 

Решение.

Поскольку угол   лежит во второй четверти, его косинус отрицателен. Поэтому



 Ответ: −0,75.