V1
|
Найти горизонтальную асимптоту функции 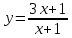 : :
|
1
|
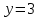
|
V1
|
Найдите предел 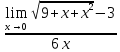
|
1
|
1/36
|
V1
|
Найдите предел 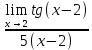 : :
|
1
|
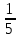
|
V1
|
Найти
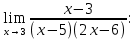
|
1
|
-1/4.
|
V1
|
Найти
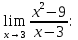
|
1
|
6
|
V1
|
Найти
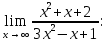
|
1
|
1/3
|
V1
|
Найти 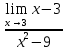
|
1
|
1/6
|
V1
|
Найти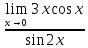 : :
|
1
|
3/2.
|
V1
|
Найти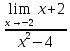
|
1
|
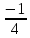
|
V1
|
Найдите область определения функции 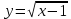 . .
|
1
|
|
V1
|
Производная функции 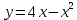 равна: равна:
|
1
|
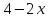 . .
|
V1
|
Найти производную функции 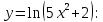
|
1
|
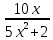 . .
|
V1
|
Найдите производную функции 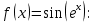
|
1
|
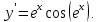
|
V1
|
Найти координату х точки минимума функции 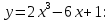
|
1
|
1.
|
V1
|
Пусть u=u(x). Тогда производная от функции tgu равна:
|
1
|
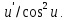
|
V1
|
Найдите производную функции 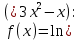
|
1
|
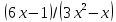
|
V1
|
Найти значение параметра p так, чтобы касательные, проведенные к линиям 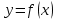 и и 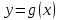 в точке в точке 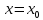 параллельны: параллельны:
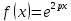
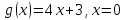
|
1
|
2
|
V1
|
Найти координаты вершины параболы у = 4х – 2х2:
|
1
|
(1,2).
|
V1
|
Найти экстремумы функции у = х3 – 9х2 + 15х.
|
1
|
ymax(1) = 7, ymin(5) = - 25.
|
V1
|
Найти интеграл 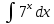
|
1
|
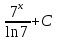
|
V1
|
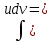 ? ?
|
1
|
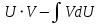
|
V1
|
Пусть 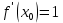 Как располагается касательная к графику функции Как располагается касательная к графику функции 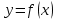 в точке в точке 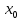 : :
|
1
|
Наклонена к оси ОХ под углом 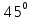 . .
|
V1
|
Найти производную функции 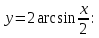
|
1
|
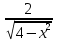
|
V1
|
Найдите предел, используя правило Лопиталя 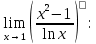
|
1
|
2.
|
V1
|
Дифференциал независимой переменной равен:
|
1
|
Приращению этой переменной.
|
V1
|
Для 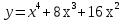 найдите значение производной в точке x=0: найдите значение производной в точке x=0:
|
1
|
0.
|
V1
|
Найти производную функции 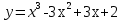 в точке в точке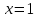 : :
|
1
|
0.
|
V1
|
Вычислить интеграл 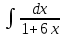 : :
|
1
|
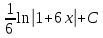
|
V1
|
Найдите неопределенный интеграл 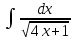 : :
|
1
|
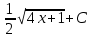 . .
|
V1
|
Неопределенный интеграл 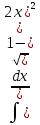 равен: равен:
|
1
|
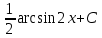
|
V1
|
Найдите неопределенный интеграл 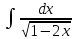 : :
|
1
|
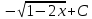
|
V1
|
Вычислите определенный интеграл  : :
|
1
|
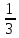
|
V1
|
Вычислите интеграл 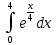 : :
|
1
|
4(е-1)
|
V1
|
Найдите неопределенный интеграл 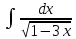 : :
|
1
|
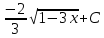
|
V1
|
Вычислить площадь фигуры, ограниченной кривыми 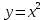 , , 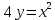 , , 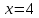 . .
|
1
|
16
|
V1
|
Вычислить интеграл 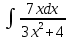 : :
|
1
|
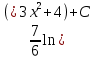
|
V1
|
Найдите площадь фигуры, ограниченной линиями 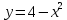 , , 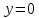 : :
|
1
|
32/3
|
V1
|
Площадь фигуры, ограниченной линиями 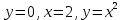 равна: равна:
|
1
|
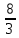
|
V1
|
С помощью определенного интеграла найти площадь фигуры, ограниченной линиями 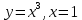 и и 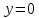
|
1
|
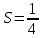
|
V1
|
Вычислить интеграл 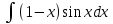 : :
|
1
|
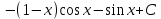
|
V1
|
Вычислить объем тела полученного вращением относительно оси Ох фигуры, ограниченной кривыми 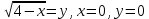
|
1
|
|
V1
|
Вычислить интеграл 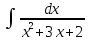 : :
|
1
|
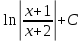
|
V1
|
Вычислить интеграл 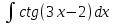 : :
|
1
|
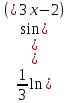
|
V1
|
Вычислить площадь, ограниченную одной полуволной 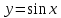 , , 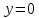 : :
|
1
|
2
|
V1
|
Площадь фигуры, ограниченной линиями 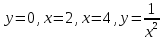 равна: равна:
|
1
|
0,25
|
V1
|
Вычислить интеграл 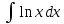 : :
|
1
|
xlnx - x+C.
|
V1
|
Вычислить интеграл 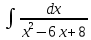 : :
|
1
|
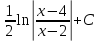
|
V1
|
Вычислить площадь, ограниченной параболой 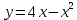 и осью абсцисс: и осью абсцисс:
|
1
|
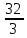
|
V1
|
Значение определенного интеграла 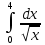 равно: равно:
|
1
|
4
|
V1
|
Площадь фигуры, ограниченной линиями 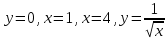 , равна: , равна:
|
1
|
2
|
V1
|
Вычислить определитель: 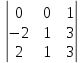
|
1
|
-4;
|
V1
|
Вычислить определитель: 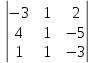
|
1
|
7;
|
V1
|
 Вычислить определитель: Вычислить определитель: 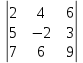
|
1
|
96;
|
V1
|
Вычислите  системы: системы: 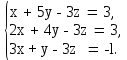
|
1
|
12.
|
V1
|
Вычислить определитель: 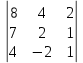
|
1
|
-24;
|
V1
|
Найти алгебраическое дополнение 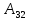 матрицы матрицы 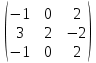 : :
|
1
|
4
|
V1
|
Как называется данное действие:
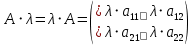
|
1
|
Умножение матрицы на число
|
V1
|
Определителем второго порядка, соответствующим данной матрице, называется
|
1
|
число
|
V1
|
Какая из приведенных ниже формул является верной?
|
1
|
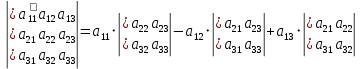
|
V1
|
Как обозначается минор для элементы а12
|
1
|
М12
|
V1
|
Какая из приведенных ниже формул является верной?
|
1
|
А*А-1 = Е
|
V1
|
Матрица, в которой меняются местами строки и столбцы называется
|
1
|
транспонированной
|
V1
|
Матрица, определитель которой не равен нулю называется
|
1
|
невырожденной
|
V1
|
Какая из приведенных ниже формул является верной?
|
1
|
Аij = (-1)i+j Mij.
|
V1
|
Вставить в данное утверждение, необходимое(пропущенной) слово: «____________, соответствующим данному элементу определителя третьего порядка, называется определитель второго порядка, полученный из данного определителя вычеркиванием той строки и того столбца, на пересечении которых стоит данный элемент»
|
1
|
минором
|
V1
|
Какому закону не подчиняется умножение матриц?
|
1
|
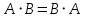
|
V1
|
При решении систем линейных уравнений, матричный метод основывается на формуле?
|
1
|
X = А-1 · B.
|
V1
|
Какое из следующих выражений показывает правило Крамера:
|
1
|
Если 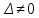 , то отсюда получаем, что исходная система имеет единственное решение: , то отсюда получаем, что исходная система имеет единственное решение:
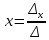 , , 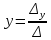
|
V1
|
Из приведенных ниже формулировок выберите верное:
|
1
|
Система имеет решения, если ранг матрицы А равен рангу расширенной матрицы В.
|
V1
|
а11x + а12y + а13z = с1,
а21x + а22 y + a23z = с2,
a31x + a32y + a33z = c3
Пусть дана система, как будет выглядеть определитель для переменной х?
|
1
|
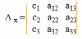
|
V1
|
а11x + а12y + а13z = с1,
а21x + а22 y + a23z = с2,
a31x + a32y + a33z = c3
Пусть дана система, как будет выглядеть определитель для переменной у?
|
1
|
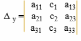
|
V1
|
В каком из свойств скалярного произведения допущена ошибка?

|
1
|
1
|
V1
|
В каком из свойств скалярного произведения допущена ошибка?

|
1
|
2 и 3
|
V1
|
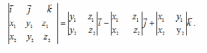
Данная формула выражает?
|
1
|
Векторное произведение двух векторов
|
V1
|
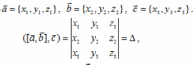
Данная формула выражает?
|
1
|
Смешанное произведение векторов
|
V1
|
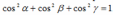
Данная формула выражает?
|
1
|
Связь между направляющими косинусами вектора
|
V1
|
Уравнение, связывающее координаты х, у точки М, называется уравнением линии L, если
|
1
|
координаты х, у любой точки М линии L удовлетворяют этому уравнению
|
V1
|
Данная формула выражает
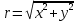 ? ?
|
1
|
Расстояние от начала координат до любой точки плоскости
|
V1
|
Пусть А(х1; у1) и В(х2; у2), тогда формулы
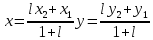 , где , где 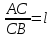
выражают:
|
1
|
Деление отрезка в данном отношении
|
V1
|
Пусть прямые заданы общими уравнениями прямых А1х+В1у+С1=0 и А2х+В2у+С2 = 0, если A1/A2 = B1/B2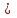 С1/С2, то С1/С2, то
|
1
|
прямые параллельны между собой.
|
V1
|
Пусть прямые заданы общими уравнениями прямых А1х+В1у+С1=0 и А2х+В2у+С2 = 0, если A1/A2 = B1/B2 = С1/C2, то
|
1
|
прямые совпадают.
|
V1
|
Пусть прямые заданы общими уравнениями прямых А1х+В1у+С1=0 и А2х+В2у+С2 = 0, если A1·A2 + B1·B2 = 0 то
|
1
|
прямые перпендикулярны.
|
V1
|
Если даны прямые у=а1х+b1, и у=а2х+b2 (линейные уравнения прямой), то если
|
1
|
а1· а2 = (-1), то прямые перпендикулярны
|
V1
|
Если даны прямые у=а1х+b1, и у=а2х+b2 (линейные уравнения прямой), то если
|
1
|
а1= а2, b1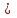 b2, то прямые параллельны b2, то прямые параллельны
|
V1
|
Как называется вид уравнения прямой? 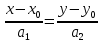
|
1
|
Каноническое
|
V1
|
Какая из ниже представленных формул, выражает уравнение прямой, проходящей через две заданные точки 𝑀1 (𝑥1,𝑦1) и 𝑀2 (𝑥2,𝑦2):
|
1
|
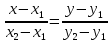 . .
|
V1
|
Пусть плоскость П заданная уравнением 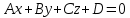 , ,
а прямая d - уравнением 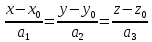 . Тогда: . Тогда:
|
1
|
Все перечисленные ответы верны.
|
V1
|
Пусть плоскость П заданная уравнением 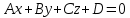 , ,
а прямая d - уравнением 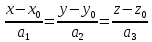 . Тогда: . Тогда:
|
1
|
плоскость П и прямая d образуют угол φ, тогда
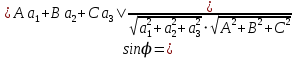
|
V1
|
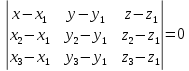 . .
Что выражает данная формула?
|
1
|
Уравнение плоскости по трём заданным точкам: 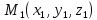 , , 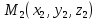 , , 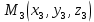
|
V1
|
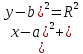 данное уравнение называется … данное уравнение называется …
|
1
|
Уравнением окружности с центром в т.С(a, b)
|
V1
|
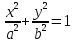 данное уравнение называется … данное уравнение называется …
|
1
|
Каноническим уравнением эллипса
|
20
V1
|
Как называется уравнение вида
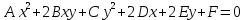
|
1
|
Алгебраическим уравнением 2 степени
|
V1
|
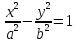 данное уравнение называется … данное уравнение называется …
|
1
|
Уравнением гиперболы
|
V1
|
Какие способы задание функции Вы знаете?
|
0
|
Аналитический
|
1
|
Все перечисленные ответы верны
|
0
|
табличный
|
0
|
Графический(геометрический)
|
0
|
Неявная функция
|
V1
|
Найдите среди представленных ниже равенств верное:
|
1
|
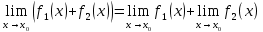
|
V1
|
Найдите среди представленных ниже равенств верное:
|
0
|
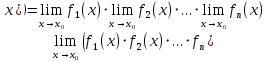
|
0
|
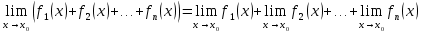
|
0
|
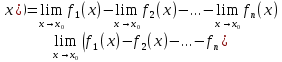
|
0
|
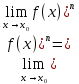
|
1
|
Все перечисленные ответы верны
|
V1
|
Какое из представленных равенств является верным
|
1
|
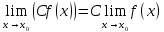
|
V1
|
Если при вычислении предела дроби 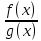 числитель и знаменатель одновременно стремятся к нулю или бесконечности, то эта дробь представляет собой неопределенность вида: числитель и знаменатель одновременно стремятся к нулю или бесконечности, то эта дробь представляет собой неопределенность вида:
|
1
|
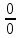 или или 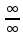
|
V1
|
Что входит в понятие «раскрыть неопределенность»?
|
1
|
Это значит преобразовать выражения таким образом, чтобы избавиться от неопределенности.
|
V1
|
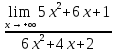 . .
Опишите метод решения для пределов данного вида.
|
1
|
Для того чтобы найти предел данной дроби, предварительно преобразуем ее, разделив числитель и знаменатель на переменную в наивысшей степени 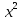 ; дробь от этого не изменит своей величины, а, следовательно, и своего предела. ; дробь от этого не изменит своей величины, а, следовательно, и своего предела.
|
V1
|
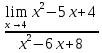 . .
Опишите метод решения для пределов данного вида.
|
1
|
Нахождение предела этой дроби сводится к раскрытию неопределенности, для этого преобразуем дробь, разложив числитель и знаменатель на множители.
|
V1
|
Данная запись 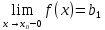 обозначает обозначает
|
1
|
Левосторонний предел
|
V1
|
Данная запись 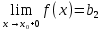 обозначает обозначает
|
1
|
Правосторонний предел
|
V1
|
Какое из ниже приведенных равенств есть определение производной
|
1
|
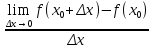
|
V1
|
Какое из представленных утверждений является верным?
|
1
|
Все утверждения являются верными
|
V1
|
Какая из ниже приведенных формул является верной для вычиcления производной сложной функции
|
1
|
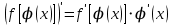 . .
|
V1
|
Найти производную функции 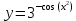
|
1
|
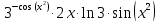
|
V1
|
Найти производную функции, заданной параметрически
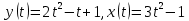
|
1
|
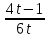
|
V1
|
Найти производную 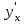 функции, заданной неявно: функции, заданной неявно:
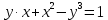
|
1
|
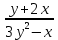
| |
 Скачать 346.93 Kb.
Скачать 346.93 Kb.