V1
|
С помощью производной найдите промежутки возрастания функции: f(x) = x3 +12.
|
1
|
(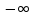 ; ;  ) )
|
V1
|
Найти производную функции: 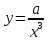
|
1
|
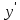 = =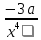
|
V1
|
Найдите производную функции: y = xsinx .
|
1
|
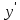 = (sinx + xcosx) = (sinx + xcosx)
|
V1
|
С помощью производной найдите промежутки возрастания функции: f(x) = 2х - 3.
|
1
|
(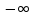 ; ;  ) )
|
V1
|
Исследуй те функцию на экстремум: f(x) = -4х2 - 6х - 7.
|
1
|
х = -3/4, точка max
|
V1
|
Исследуйте функцию на экстремум: f(x) = 3 + 4х - х2.
|
1
|
х = 2, точка max
|
V1
|
Производная второго порядка используется при исследовании функции для нахождения?
|
1
|
промежутков выпуклости и вогнутости графика функции;
|
V1
|
Если x = f(t) закон прямолинейного движения точки, то x″ = f″ (t)
|
1
|
ускорение данного движения;
|
V1
|
Составьте уравнение касательной к графику функции у = -3x2 + 6x + 1 в точке пересечения этого графика с осью ординат.
|
1
|
y=6x+1
|
V1
|
Найти тангенс угла наклона касательной к графику функции f(x) = 2x3 - 5x в точке М(2; 6).
|
1
|
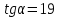
|
V1
|
Найдите производную второго порядка от функции f(х) = ех−5х3.
|
1
|
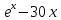
|
V1
|
Найдите производную следующей функции: 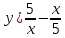 . .
|
1
|
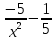
|
V1
|
Найдите 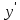 : y = (1 – 3x2)(1 - x)3. : y = (1 – 3x2)(1 - x)3.
|
1
|
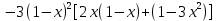
|
V1
|
Найдите 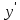 : y = ln(x2+1). : y = ln(x2+1).
|
1
|
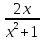
|
V1
|
Найдите в точке х=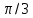 значение производной функции значение производной функции
f(x) = cos2 x.
|
1
|
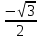
|
V1
|
Найдите минимум функции f(x) = х2(х -3).
|
1
|
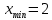
|
V1
|
Производная функции f(x)= 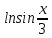 равна. равна.
|
1
|
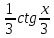
|
V1
|
Точкой, в которой выполняется необходимое условие существования экстремума функции y=3x4 – 4x3, но экстремума нет, является:
|
1
|
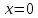
|
V1
|
Если 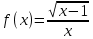 , то f ’ (2)= … , то f ’ (2)= …
|
1
|
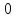
|
V1
|
К графику функции f(x) = 5x3 + 9x – 27 в точке с абсциссой x = 0 проведена касательная. Найдите абсциссу точки пересечения касательной с осью Ox.
|
1
|
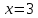
|
V1
|
Чему равна первая производная функции 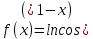 ? ?
|
1
|
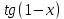
|
V1
|
Для функции 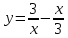 , определите: а) нули; б) промежутки возрастания; в) промежутки убывания. , определите: а) нули; б) промежутки возрастания; в) промежутки убывания.
|
1
|
c) 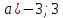 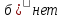 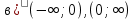
|
V1
|
Найдите наибольшее и наименьшее значения функции
y(x) = x2 –11x+28 на отрезке [4; 5].
|
1
|
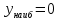 ; ; 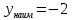
|
V1
|
Найдите уравнение касательной к графику функции f(x) = 2x2 – 1, проходящей через точку (0; -1).
|
1
|
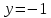
|
V1
|
Найдите наибольшее и наименьшее значения функции 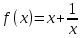 на заданном отрезке на заданном отрезке 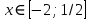 . .
|
1
|
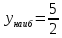 ; ; 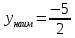
|
V1
|
Какой угол с осью Ох образует касательная к графику функции 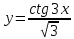 в точке в точке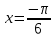 . .
|
1
|
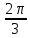
|
V1
|
Напишите уравнение касательной к графику функции
y = cos4x – 1 в точке Мо 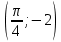 . .
|
1
|
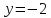
|
V1
|
Напишите уравнение касательной к графику функции
y = cos2x + 2 в точке Мо 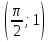 . .
|
1
|
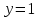
|
V1
|
Найти производную функции 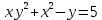 . .
|
1
|
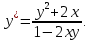
|
V1
|
Найти дифференциал второго порядка функции 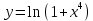
|
1
|
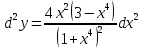
|
40
V1
|
Вычислить предел 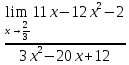 по правилу Лопиталя: по правилу Лопиталя:
|
1
|
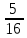
|
V1
|
Вычислить предел по правилу Лопиталя: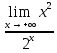
|
1
|
0
|
V1
|
Точка, отделяющая выпуклую часть непрерывной кривой от вогнутой, называется
|
1
|
точкой перегиба кривой.
|
V1
|
Если во всех точках интервала 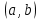 вторая производная функции вторая производная функции 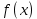 существует и отрицательна, т.е. существует и отрицательна, т.е. 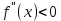 , то кривая , то кривая 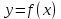 на этом интервале ___________. на этом интервале ___________.
|
1
|
выпукла
|
V1
|
Найти производную функции 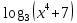
|
1
|
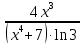
| |
 Скачать 346.93 Kb.
Скачать 346.93 Kb.