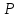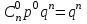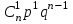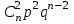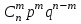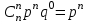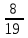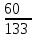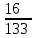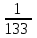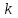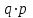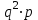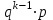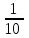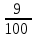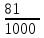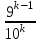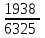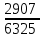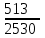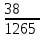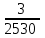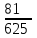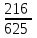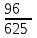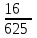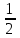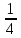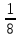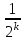Порно собак. Виды распределения ДСВ. Виды распределения дискретных случайных величин
 Скачать 306.58 Kb. Скачать 306.58 Kb.
|
|
Тема: «Виды распределения дискретных случайных величин» Ниже приведены важнейшие законы распределения для дискретных случайных величин Биномиальный закон распределения дискретной случайной величины Дискретная случайная величина  имеет биномиальное распределение (или распределена по биномиальному закону), если она принимает значения 0, 1, 2, 3, …, имеет биномиальное распределение (или распределена по биномиальному закону), если она принимает значения 0, 1, 2, 3, …, 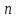 с вероятностями: с вероятностями: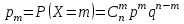 , ,где 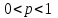 , , 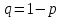 , , 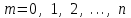 . .Случайная величина  , распределённая по биномиальному закону, является числом «успехов» с вероятностью , распределённая по биномиальному закону, является числом «успехов» с вероятностью 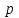 в схеме Бернулли при проведении в схеме Бернулли при проведении 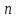 независимых опытов. независимых опытов.Закон распределения дискретной случайной величины  , имеющей биномиальное распределение, имеет вид: , имеющей биномиальное распределение, имеет вид:
Математическое ожидание дискретной случайной величины, имеющей биномиальное распределение, можно вычислить по формуле: 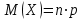 . .Дисперсию дискретной случайной величины, имеющей геометрическое распределение, можно вычислить по формуле: 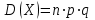 . .Среднее квадратическое отклонение дискретной случайной величины, имеющей геометрическое распределение, можно вычислить по формуле: 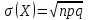 . .Пример Производится 3 независимых выстрела по цели. Вероятности попадания при разных выстрелах одинаковы и равны 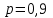 . Составить закон распределения дискретной случайной величины . Составить закон распределения дискретной случайной величины  – числа попаданий по цели. Найти – числа попаданий по цели. Найти 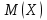 , , 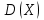 и и 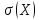 . .Случайная величина  имеет биномиальное распределение с параметрами имеет биномиальное распределение с параметрами 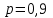 , , 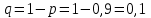 , , 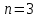 . .Случайная величина  принимает значения 0, 1, 2 и 3. Вероятности этих значений принимает значения 0, 1, 2 и 3. Вероятности этих значений 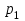 , , 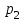 , , 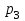 и и 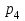 найдём по формуле для вероятностей биномиального распределения: найдём по формуле для вероятностей биномиального распределения: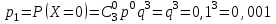 ; ;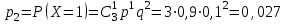 ; ;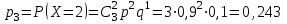 ; ;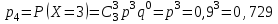 . .Составим закон распределения дискретной случайной величины  – числа попаданий по цели: – числа попаданий по цели:
Контроль: 0,001+0,027+0,243+0,729=1. Значения 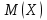 , , 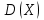 и и 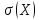 найдём двумя способами: а) по закону распределения; б) по готовым формулам. найдём двумя способами: а) по закону распределения; б) по готовым формулам.а) 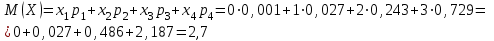 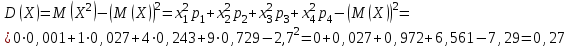 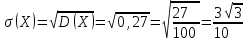 б) 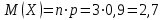 ; ;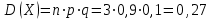 ; ;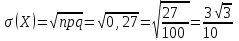 . .Гипергеометрический закон распределения дискретной случайной величины Дискретная случайная величина  имеет гипергеометрическое распределение, если она принимает значения 0, 1, 2, …, имеет гипергеометрическое распределение, если она принимает значения 0, 1, 2, …, 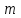 , …, , …, 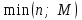 с вероятностями: с вероятностями: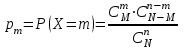 , ,где 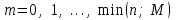 , , 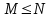 , , 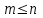 , , 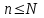 , а , а 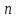 , , 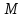 и и 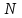 – натуральные числа. – натуральные числа.Гипергеометрическое распределение возникает в случаях, подобных следующему: в урне 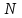 шаров, из них шаров, из них 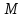 белых (остальные белых (остальные 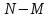 чёрные); из урны вынимается чёрные); из урны вынимается 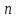 шаров. Требуется найти вероятность, что среди извлечённых шаров ровно шаров. Требуется найти вероятность, что среди извлечённых шаров ровно 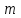 белых (остальные белых (остальные 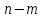 чёрные). Случайная величина чёрные). Случайная величина  – число белых шаров среди извлечённых из урны. – число белых шаров среди извлечённых из урны.Математическое ожидание дискретной случайной величины, имеющей гипергеометрическое распределение, можно вычислить по формуле: 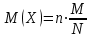 . .Дисперсию дискретной случайной величины, имеющей гипергеометрическое распределение, можно вычислить по формуле: 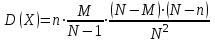 . .Пример В классе из 21 ученика 5 девушек. Из этого класса наудачу отбирается 3 ученика. Составить закон распределения дискретной случайной величины  – числа девушек из отобранных учеников. Найти – числа девушек из отобранных учеников. Найти 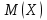 и и 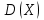 . .В условиях данной задачи: 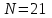 , , 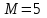 , , 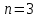 . Случайная величина . Случайная величина  принимает значения 0, 1, 2 и 3. Вероятности этих значений принимает значения 0, 1, 2 и 3. Вероятности этих значений 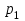 , , 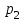 , , 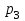 и и 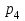 найдём по формуле для вероятностей гипергеометрического распределения: найдём по формуле для вероятностей гипергеометрического распределения: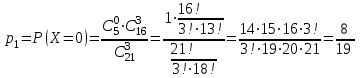 ; ;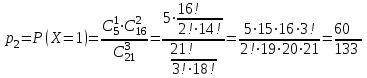 ; ;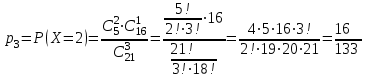 ; ;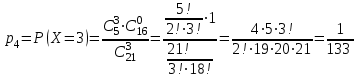 . .Составим закон распределения дискретной случайной величины  – числа девушек из 3 отобранных учеников: – числа девушек из 3 отобранных учеников:
Контроль: 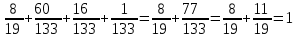 . .Значения 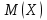 и и 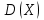 найдём двумя способами: а) по закону распределения; б) по готовым формулам. найдём двумя способами: а) по закону распределения; б) по готовым формулам.а) 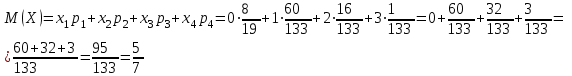 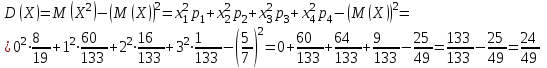 б) 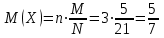 ; ;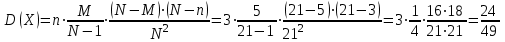 . .Геометрический закон распределения дискретной случайной величины Дискретная случайная величина  имеет геометрическое распределение, если она принимает значения 1, 2, 3, 4, … с вероятностями: имеет геометрическое распределение, если она принимает значения 1, 2, 3, 4, … с вероятностями: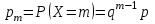 , ,где 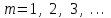 Геометрическое распределение имеет случайная величина  , равная числу опытов в схеме Бернулли, проведённой до первого «успеха» (в единичном опыте вероятность «успеха»: , равная числу опытов в схеме Бернулли, проведённой до первого «успеха» (в единичном опыте вероятность «успеха»: 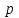 , вероятность «неудачи»: , вероятность «неудачи»: 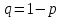 ). ).Примерами реальных случайных величин, распределённых по геометрическому закону, являются: число выстрелов до первого попадания; число испытаний прибора до первого отказа; число бросаний монеты до первого выпадения герба и т.д. Закон распределения случайной величины  , имеющей геометрическое распределение, имеет вид: , имеющей геометрическое распределение, имеет вид:
Контроль: 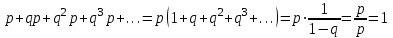 . .Вероятности 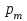 образуют геометрическую прогрессию, по этой причине данное распределение называют геометрическим. образуют геометрическую прогрессию, по этой причине данное распределение называют геометрическим.Математическое ожидание дискретной случайной величины, имеющей геометрическое распределение, можно вычислить по формуле: 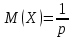 . .Дисперсию дискретной случайной величины, имеющей геометрическое распределение, можно вычислить по формуле: 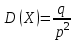 . .Среднее квадратическое отклонение дискретной случайной величины, имеющей геометрическое распределение, можно вычислить по формуле: 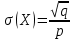 . .Пример Вероятность попадания в цель при отдельном выстреле для данного стрелка равна 0,1. Составить закон распределения дискретной случайной величины  – числа выстрелов по цели до первого попадания. Найти – числа выстрелов по цели до первого попадания. Найти 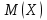 , , 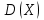 и и 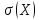 . .Случайная величина  имеет геометрическое распределение с параметрами имеет геометрическое распределение с параметрами 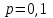 и и 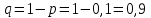 . Вероятности значений, принимаемых случайной величиной найдём по формуле для вероятностей геометрического распределения: . Вероятности значений, принимаемых случайной величиной найдём по формуле для вероятностей геометрического распределения: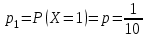 ; ;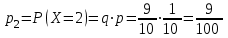 ; ;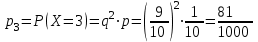 ; ;… 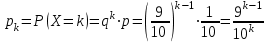 ; ;… Составим закон распределения дискретной случайной величины  – числа выстрелов по цели до первого попадания: – числа выстрелов по цели до первого попадания:
Значения 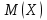 , , 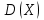 и и 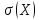 найдём по готовым формулам. найдём по готовым формулам.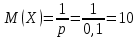 ; ;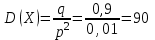 ; ;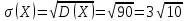 . .Задачи 1. Из 25 контрольных работ, среди которых 6 оценены на «отлично», наугад извлекают 4 работы. Составьте закон распределения дискретной случайной величины  – числа оценённых на «отлично» работ среди четырёх извлечённых. Найти – числа оценённых на «отлично» работ среди четырёх извлечённых. Найти 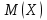 , , 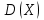 и и 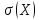 . .Решение Данная случайная величина имеет гипергеометрическое распределение с параметрами: 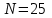 , , 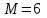 , , 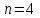 . Случайная величина . Случайная величина  принимает значения 0, 1, 2, 3 и 4, так как среди четырёх извлечённых контрольных работ может не быть оценённых на «отлично», а могут и всё 4 быть оценёнными на «отлично». Вероятности этих значений принимает значения 0, 1, 2, 3 и 4, так как среди четырёх извлечённых контрольных работ может не быть оценённых на «отлично», а могут и всё 4 быть оценёнными на «отлично». Вероятности этих значений 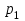 , , 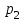 , , 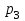 , , 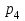 и и 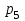 найдём по формуле для вероятностей гипергеометрического распределения: найдём по формуле для вероятностей гипергеометрического распределения: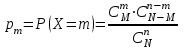 . .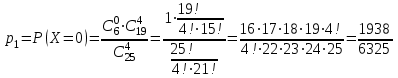 ; ;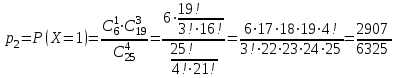 ; ;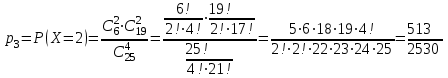 ; ;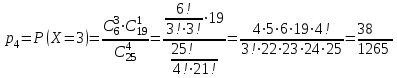 ; ;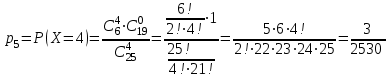 . .Составим закон распределения дискретной случайной величины  – числа оценённых на «отлично» работ среди четырёх извлечённых: – числа оценённых на «отлично» работ среди четырёх извлечённых:
Контроль: 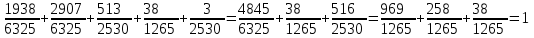 . .Значения 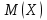 , , 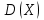 и и 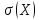 найдём двумя способами: а) по закону распределения; б) по готовым формулам. найдём двумя способами: а) по закону распределения; б) по готовым формулам.а) 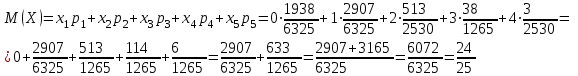 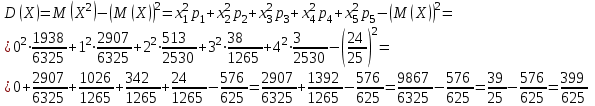 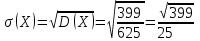 б) 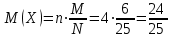 ; ;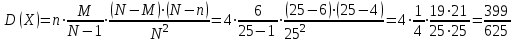 ; ;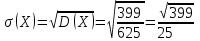 . .Ответ: 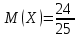 ; ; 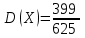 ; ; 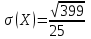 . .2. Вероятность попадания баскетбольным мячом в корзину при одном броске равна 0,4. Составьте закон распределения дискретной случайной величины  – числа попадания мячом в корзину при четырёх бросках. Найти – числа попадания мячом в корзину при четырёх бросках. Найти 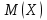 , , 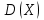 и и 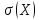 . .Решение Броски производятся независимо друг от друга, вероятность попадания при разных бросках одинакова и равна 0,4. Значит, имеет место схема Бернулли, в которой «успехом» считается попадание, а «неудачей» – промах. Следовательно, случайная величина  , равная числу попаданий мячом в корзину при четырёх бросках, имеет биномиальное распределение с параметрами , равная числу попаданий мячом в корзину при четырёх бросках, имеет биномиальное распределение с параметрами 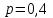 , , 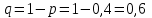 , , 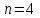 . .Случайная величина  принимает значения 0, 1, 2, 3 и 4. Вероятности этих значений принимает значения 0, 1, 2, 3 и 4. Вероятности этих значений 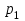 , , 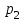 , , 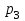 , , 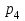 и и 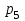 найдём по формуле для вероятностей биномиального распределения: найдём по формуле для вероятностей биномиального распределения: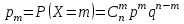 . .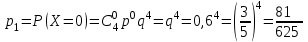 ; ;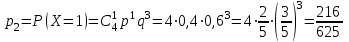 ; ;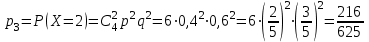 ; ;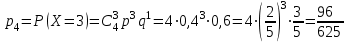 ; ;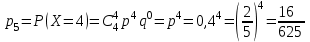 Составим закон распределения дискретной случайной величины  – числа попаданий по цели: – числа попаданий по цели:
Контроль: 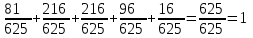 . .Значения 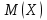 , , 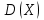 и и 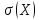 найдём двумя способами: а) по закону распределения; б) по готовым формулам. найдём двумя способами: а) по закону распределения; б) по готовым формулам.а) 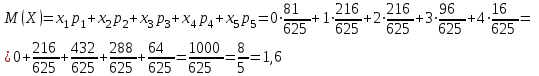 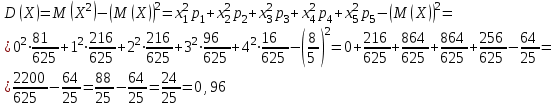 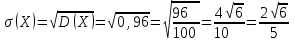 б) 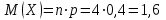 ; ;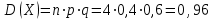 ; ;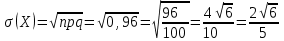 . .Ответ: 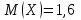 ; ; 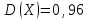 ; ; 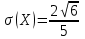 . .3. Симметричная однородная монета подбрасывается до первого выпадения герба. Составьте закон распределения дискретной случайной величины  – числа подбрасываний монеты. Найти – числа подбрасываний монеты. Найти 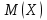 , , 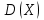 и и 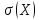 . .Решение Подбрасывания монеты производятся независимо друг от друга, вероятность выпадения при разных подбрасываниях одинакова и равна 0,5. Значит, имеет место схема Бернулли, в которой «успехом» считается выпадение герба, а «неудачей» – выпадение цифры. Так как подбрасывания производятся до первого выпадения герба, то случайная величина  , равная числу подбрасываний монеты, имеет геометрическое распределение с параметрами , равная числу подбрасываний монеты, имеет геометрическое распределение с параметрами 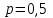 и и 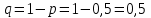 . Вероятности значений, принимаемых случайной величиной найдём по формуле для вероятностей геометрического распределения: . Вероятности значений, принимаемых случайной величиной найдём по формуле для вероятностей геометрического распределения: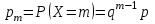 . .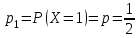 ; ;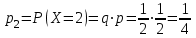 ; ;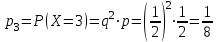 ; ;… 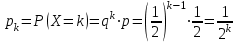 ; ;… Составим закон распределения дискретной случайной величины  – числа выстрелов по цели до первого попадания: – числа выстрелов по цели до первого попадания:
Значения 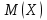 , , 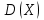 и и 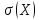 найдём по готовым формулам. найдём по готовым формулам.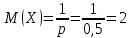 ; ;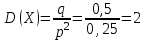 ; ;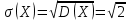 . .Ответ: 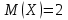 ; ; 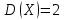 ; ; 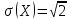 . .!!! Задания для самостоятельного решения (домашнее задание) – фото выслать на электронный адрес mdutkin@mail.ru до 18.00 воскресенья 17 мая: 1. Контрольная работа по теории вероятностей состоит из пяти задач. Вероятность решить правильно каждую задачу для данного ученика равна 0,7. Составьте закон распределения дискретной случайной величины  – числа правильно решённых задач. Найти – числа правильно решённых задач. Найти 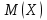 , , 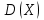 и и 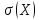 . .2. В офисе работают 8 мужчин и 4 женщины. Для работы над проектом создаётся рабочая группа, состоящая из 7 человек. Составьте закон распределения дискретной случайной величины  – числа женщин в создаваемой рабочей группе. Найти – числа женщин в создаваемой рабочей группе. Найти 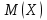 , , 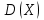 и и 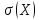 . .3. Азартный человек покупает лотерейные билеты до первого выигрыша. По условиям лотереи вероятность выигрыша по одному билету равна 0,2. Составьте закон распределения дискретной случайной величины  – числа купленных билетов, если теоретически можно купить неограниченное количество билетов. Найти – числа купленных билетов, если теоретически можно купить неограниченное количество билетов. Найти 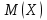 , , 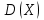 и и 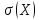 . .4. Азартный человек покупает лотерейные билеты до первого выигрыша. По условиям лотереи вероятность выигрыша по одному билету равна 0,2. Составьте закон распределения дискретной случайной величины  – числа купленных билетов, если можно купить только 4 билета. Найти – числа купленных билетов, если можно купить только 4 билета. Найти 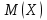 , , 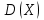 и и 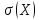 . . |