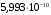Проектирование Высоковольтного ввода. Мой ввод. Высоковольтный ввод конденсаторного типа
 Скачать 1.31 Mb. Скачать 1.31 Mb.
|
2.13 Определение емкостей слоевЕмкость в k-ом слое определяется по формуле: 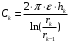 (2.26) (2.26)где 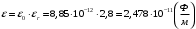 Для первого слоя емкость составит: 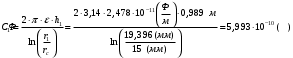 (2.27) (2.27) Таблица.4 Значения емкостей слоев
Общая емкость изоляционного остова (всех слоев) составит 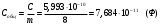 (2.28) (2.28)2.14 Вычисление максимальных и минимальных радиальных напряженностей в слояхМаксимальная и минимальная напряженности могут быть определены из следующих соотношений:  (2.29) (2.30) (2.29) (2.30)Для первого слоя: 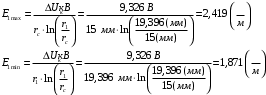 (2.31) (2.31)Остальные величины напряженностей слоев приведены в табл. 5. Таблица.5 Значения напряженностей слоев
По полученным данным строим график распределения радиальных напряженностей по слоям, по оси абсцисс которого откладывается радиус слоя, а по оси ординат – значение напряженности, соответствующей этому радиусу  Рис. 4. График распределения радиальных напряженностей. Из расчета видно, что напряженность в каждом слое не превышает допустимое значение 4 кВ/мм, максимальные напряженности в первом и восьмом слоях приблизительно равны рабочему значению напряженности (Ераб=4 кВ/мм) и напряженность вблизи поверхности трубы (Еrc=2,42 кВ/мм) не превышает допустимого значения. Это говорит о том, что электрический расчет выполнен верно. 3. ТЕПЛОВОЙ РАСЧЕТ При расчёте тепловой устойчивости проходного изолятора выясняется возможность развития теплового пробоя в проектируемой конструкции при заданном токе, проходящем по токоведущему стержню, и наибольшем допустимом напряжении. Так как аксиальные размеры изолятора существенно больше радиальных, при проведении теплового расчёта принимают, что тепловое поле изолятора радиально, т.е. вся теплоотдача осуществляется только в радиальном направлении (рис. 3.1). 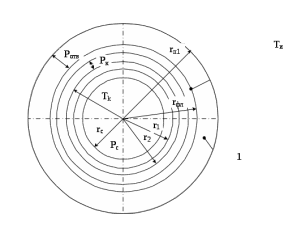 Рис. 5. Схема для графического расчёта тепловой устойчивости изолятора конденсаторного типа: 1–полимер Расчёт выполняется для установившегося теплового режима изоляции. Исходными данными при расчёте являются ток в стержне изолятора, температура окружающей среды и зависимость tg от температуры для применяемой изоляции. Расчёт производится методом «шаг за шагом». Для проведения расчёта задаются рядом значений температуры стержня Тс1, Тс2, …, Тсn. Эти значения произвольны, но должны быть близки к возможной искомой температуре стержня Тс при данных условиях. Практически для изоляторов высокого напряжения удобно принять значения Тс равными 40, 60, 80 и 100 С. Найдем тепловые сопротивления полимерной покрышки и окружающей среды. Принимаем толщину полимерной стенки изолятора – Δп = 20 мм, тогда: 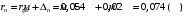 (3.1) (3.1)Тепловое сопротивление полимерной покрышки: 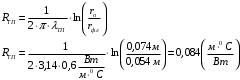 (3.2) (3.2)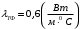 - коэффициент теплопроводности полимера. - коэффициент теплопроводности полимера.Для расчёта теплоотдачи ввода в окружающую среду принимается коэффициент теплоотдачи с поверхности полимера kтв = 20 Вт/(м2 С), тогда: 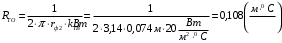 (3.3) (3.3)Определим полный тепловой поток изолятора и соответствующей ему температуры внешней поверхности изолятора. Найдем потери в токоведущем стержне: 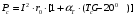 , где (3.4) , где (3.4)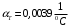 - температурный коэффициент сопротивления медного стержня; - температурный коэффициент сопротивления медного стержня;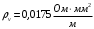 - удельное объемное сопротивление медного стержня; - удельное объемное сопротивление медного стержня;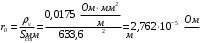 - активное сопротивление стержня; - активное сопротивление стержня;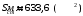 - сечение стержня. - сечение стержня.Для теплового расчета изолятора требуется значение tg δ в диапазоне температур от 40 до 100 оС. Для данного ввода применяется tg δ = f(T) зависимостью вида: tg δ = A·exp(B·T). Определим тангенс угла диэлектрических потерь комбинированной изоляции. Для RIN tg δ и εr рассчитываются по формулам: 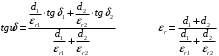 , (3.5) , (3.5)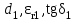 – соответственно толщина, относительная диэлектрическая проницаемость и тангенс угла диэлектрических потерь нетканый материал; – соответственно толщина, относительная диэлектрическая проницаемость и тангенс угла диэлектрических потерь нетканый материал;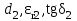 – соответственно толщина, относительная диэлектрическая проницаемость и тангенс угла диэлектрических потерь эпоксидного компаунда. – соответственно толщина, относительная диэлектрическая проницаемость и тангенс угла диэлектрических потерь эпоксидного компаунда.Для бумаги и масла можно принять r1 = 3,3, r2 = 3. Предполагая, что нетканый материал пористый и все поры бумаги заполнены пропитывающим составом, имеем: 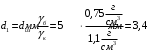 (3.6) (3.6) 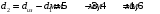 (3.7) (3.7)где б, к – плотность бумаги и клетчатки соответственно, dиз – полная толщина изоляции. При температуре 20С тангенс угла диэлектрических потерь для нетканого материала и эпоксидного компаунда равны соответственно 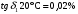 и и 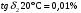 , тогда тангенс угла диэлектрических потерь комбинированного диэлектрика при 20С будет равен: , тогда тангенс угла диэлектрических потерь комбинированного диэлектрика при 20С будет равен: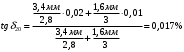 Тогда тангенс угла диэлектрических потерь комбинированного диэлектрика при 90С будет равен: 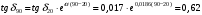  -температурный коэффициент, равный 0,0186 -температурный коэффициент, равный 0,0186Определим r комбинированного диэлектрика: 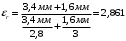 . (3.8) . (3.8)Аппроксимируем зависимость 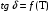 зависимостью вида зависимостью вида 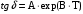 . Зная значения . Зная значения 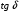 и T для двух точек зависимости можно определить коэффициенты A и B: и T для двух точек зависимости можно определить коэффициенты A и B: 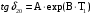 , , 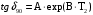 , тогда: , тогда: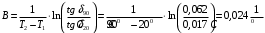 (3.9) (3.9)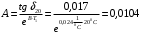 (3.10) (3.10)Исходя из полученных данных зависимость примет вид: 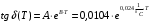 (3.11) (3.11)Ниже приведен график данной зависимости. 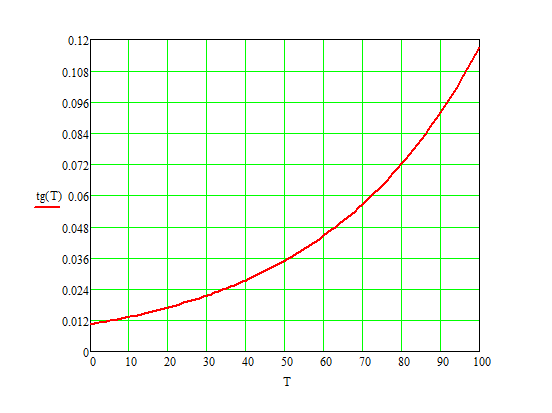 Рис. 6. Зависимость тангенса угла диэлектрических потерь от температуры. Исходными данными для теплового расчёта являются номинальный ток Iн = 1000 А, температура окружающей среды T0 = 35C, а также результаты электрического расчёта. На первом шаге задаёмся температурой стержня изолятора Tc = 40 C. Тогда электрические потери в стержне составят: 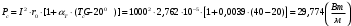 (3.12) (3.12)На втором шаге задаёмся температурой стержня изолятора Tc = 60 C. Тогда электрические потери в стержне составят: 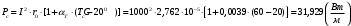 На третьем шаге задаёмся температурой стержня изолятора Tc = 80 C. Тогда электрические потери в стержне составят: 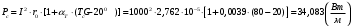 На четвертом шаге задаёмся температурой стержня изолятора Tc = 100 C. Тогда электрические потери в стержне составят: 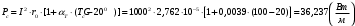 1-й слой Диэлектрические потери в изоляции первого слоя: 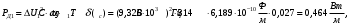 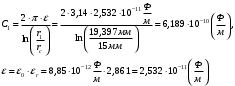 (3.13) (3.13)Определим тепловое сопротивление первого слоя на единицу длины при коэффициенте теплопроводности бумажно-масляной изоляции, равном kб = 0,17 Вт/м·оС: 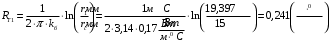 (3.14) (3.14)Перепад температуры в первом слое составит: 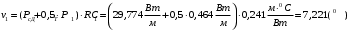 (3.15) (3.15)Найдем тепловой поток, проходящий через изоляцию первого слоя: 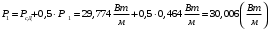 (3.16) (3.16)Температура первой обкладки будет равна: 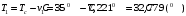 (3.17) (3.17)2-й слой Диэлектрические потери в изоляции второго слоя: 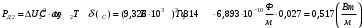 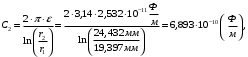 Определим тепловое сопротивление второго слоя на единицу длины при коэффициенте теплопроводности бумажно-масляной изоляции, равном kб = 0,17 Вт/м·оС: 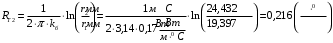 Перепад температуры во втором слое составит: 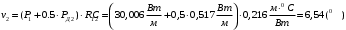 Найдем тепловой поток, проходящий через изоляцию второго слоя: 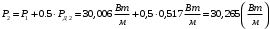 Температура второй обкладки будет равна: 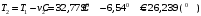 . .Аналогично расчет ведется для остальных слоев изоляции. Далее определяем полный тепловой поток Ри, проходящий через бумажно-масляную изоляцию и остальные элементы цилиндрической системы изолятора, а также температуру внешней поверхности изоляции Ти: 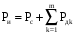 (3.18) (3.18)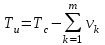 (3.19) (3.19)По такой же методике «шаг за шагом» просчитываются аналогичные параметры при Тс = 60, 80 и 100 С. Результаты теплового расчета сведены в табл. 6 и табл.7 По полученным данным строится зависимость Ри = f(Ти), а затем зависимость количества тепла, отводимого в единицу времени от наружной поверхности бумажно-масляной изоляции в окружающую среду, от температуры наружной поверхности Ти. Эта зависимость определяется соотношением 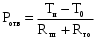 , (3.20) , (3.20)для температуры 40 С: 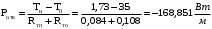 Pотв аналогично рассчитывается для Тс = 40, 60, 80 и 100 С. Полученные зависимости приведены на рис. 8. Таблица 6. Тепловой расчет проходного изолятора
Таблица.7 Результаты теплового расчета
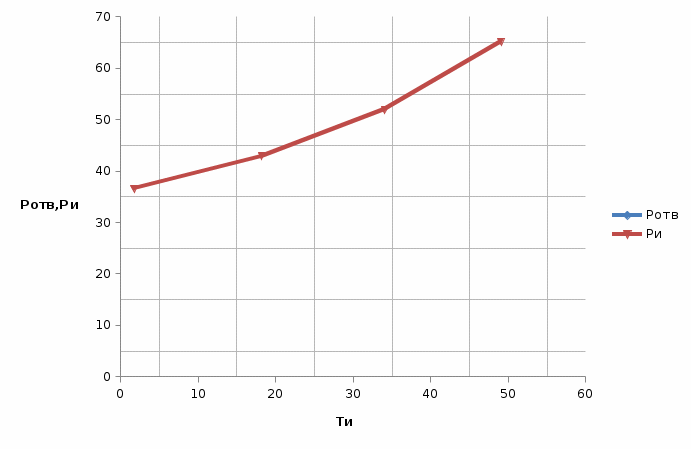 Рис. 8. Зависимость полного теплового потока через изолятор и отводимой мощности от температуры наружной поверхности. Точкой устойчивого теплового равновесия является точка пересечения. Соответственно, из графика видно, что наличие точки говорит о возможности устойчивого теплового состояния. ЗАКЛЮЧЕНИЕВ данном курсовом проекте был рассчитан высоковольтный ввод конденсаторного типа герметичного исполнения с RIN изоляцией, предназначенный для установки на выключатели (ГКПВ-III-60-110/1000-УХЛ1). Номинальное напряжение ввода 110 кВ и номинальный ток 1000 А. В работе был произведен электрический расчет с учетом постоянной аксиальной составляющей для первого варианта проектирования. Согласно результатам первого варианта проектирования, было получено 8 слоев изоляции остова высоковольтного ввода, их толщина, а так же емкость и падение напряжения на каждом слое, максимальные и минимальные напряженности слоев. Максимальная напряженность составила 2,42 кВ/мм, что не превышает допустимую напряженность, равную 4 кВ/мм. У токоведущего медного стержня был принят диаметр 30 мм. Конструкция обеспечивает надежную герметизацию ввода. Измерительный вывод от последней уравнительной обкладки остова служит для контроля характеристик внутренней изоляции. В ходе теплового расчета были определены тепловые сопротивления полимерной покрышки и окружающей среды, построена зависимость тангенса диэлектрических потерь от температуры, определено распределение температуры по слоям. В тепловом расчёте определялось выделяемое и отводимое тепло. В результате была построена зависимость полного теплового потока через изолятор и отводимой мощности от температуры наружной поверхности и определена точка устойчивого теплового равновесия. Исходя из этого, был сделан вывод, что тепловой пробой маловероятен. Библиографический список1. Электрический и тепловой расчет высоковольтных вводов/ Г.А. Филиппов, М.Е. Тихов Изоляция установок высокого напряжения: учеб. для вузов / Г.С.Кучинский, .Е. Кизиветер, Ю.С. Пинталь; под общ. ред. Г.С. Кучинского.– М.:Энергоатомиздат, 1987. –368 с. ГОСТ 1516.3-96 Электрооборудование переменного тока на напряжение от 3 до 750 кВ. Требования к электрической прочности изоляции. ГОСТ 10693-81 Вводы конденсаторные герметичные на номинальное напряжение 110 кВ и выше. Общие технические условия. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||