Пересдача реферата по матиматике. Высшая математика Реферат Тема Решение балансовых уравнений с помощью обратной матрицы. Олейник Лилия Вячеславовна
 Скачать 114.62 Kb. Скачать 114.62 Kb.
|
Автономная некоммерческая образовательная организация высшего образования «Сибирский институт бизнеса и информационных технологий»Зачетная (экзаменационная) работа (1 семестра) Дисциплина: Высшая математика Реферат Тема: Решение балансовых уравнений с помощью обратной матрицы. Выполнила: Олейник Лилия Вячеславовна (Ф.И.О. студента) (направление, группа) Проверил(а):  (Ф.И.О. преподавателя)  (дата) Омск 2022 Балансовое уравнение появляется в линейной модели экономики (модели Леонтьева) и может применяться для анализа и планирования деятельности предприятия, отрасли, а также экономики страны в целом. Рассмотрим суть этой модели на простейшем примере. Предприятие производит три вида продукции в количестве 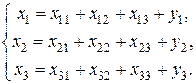 или или 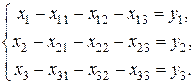 Здесь  , то можно найти, сколько продукции второго вида расходуется при производстве единицы продукции третьего вида. Аналогично, отношение , то можно найти, сколько продукции второго вида расходуется при производстве единицы продукции третьего вида. Аналогично, отношение 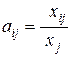 и учитывая, что и учитывая, что  , перепишем вторую систему в виде: , перепишем вторую систему в виде: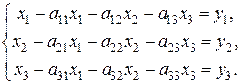 Введем в рассмотрение три матрицы: матрицу А, составленную из технологических коэффициентов (технологическую матрицу или матрицу Леонтьева), матрицу X, характеризующую выпуск продукции (производственный вектор) и матрицу Y (вектор товарной продукции или конечного спроса). 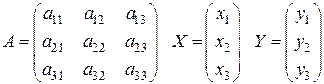 Используя введенные обозначения и помня правила действий с матрицами, систему можно записать в матричном виде: Составленное матричное уравнение и называется балансовым уравнением, его решение можно найти с помощью обратной матрицы: Применить его можно следующим способом. По результатам деятельности предприятия за истекший период составляют балансовое уравнение и находят матрицу Матрицу Рассмотрим пример решения задачи с использованием модели Леонтьева. Результаты деятельности некоторого предприятия, состоящего из трех цехов, каждый из которых производит свой вид продукции, представлены следующей таблицей.
Вычислим технологические коэффициенты и составим технологическую матрицу А. 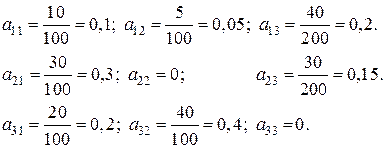 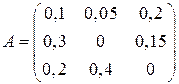 . .Составим балансовое уравнение 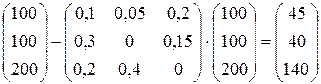 . .Выполним действия в левой части уравнения: 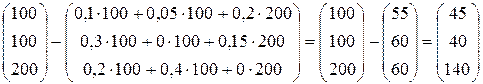 . .Т.к. левая часть уравнения равна правой, значит, уравнение составлено верно. 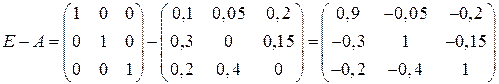 . .Вычислим матрицу полных производственных затрат а) по формуле обратной матрицы: 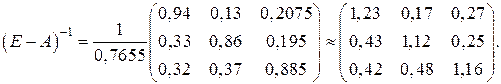 б) по приближенной формуле 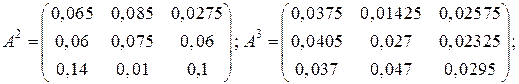 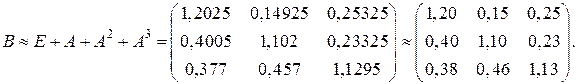 Определим новый производственный план, задав 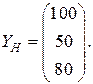 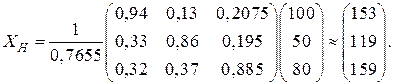 Под прямоугольными понимают такие системы линейных уравнений, в которых число уравнений не равно числу неизвестных. Число уравнений может превышать число неизвестных, а может быть меньше его. Если в системе число уравнений превышает число неизвестных то возможны два случая. Первый: часть уравнений является следствием других уравнений, их можно отбросить, система станет или квадратной или число уравнений в ней будет меньше числа неизвестных. Второй: часть уравнений противоречит другим уравнениям, такая система несовместна, не имеет решения. Решение квадратных систем линейных уравнений подробно рассматривалось, поэтому рассмотрим решение систем, в которых число уравнений меньше числа неизвестных. К составлению подобных систем приводит математическое моделирование многих экономических задач. Решение прямоугольных систем имеет свои особенности. В квадратных системах, т.е. системах, в которых число уравнений равно числу неизвестных, решением является единственный набор числовых значений неизвестных, обращающих все уравнения системы в тождества. В прямоугольных системах решение получается в виде соотношений между одними неизвестными, называемыми базисными, и другими, называемыми свободными. Поскольку свободные переменные могут принимать любые значения, а базисные переменные меняются в зависимости от них, то, по сути, прямоугольные системы имеют бесконечное множество числовых решений. Рассмотрим пример. Найти решение системы линейных уравнений 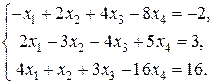 при различных способах выбора базиса. Выберем в качестве базисных неизвестные 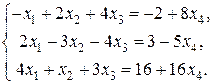 Эту систему можно решать как квадратную, например, методом Гаусса. Чтобы исключить 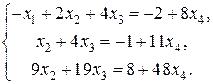 Чтобы исключить 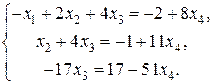 Разделим обе части третьего уравнения на (-17) и найдем Итак, решение системы при первом способе выбора базиса: 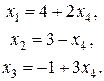 Для проверки найденное решение подставим во все уравнения исходной системы. 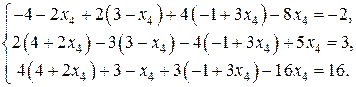 Раскрывая скобки и приводя подобные, убеждаемся, что все уравнения системы обращаются в тождества. Выберем теперь в качестве базисных переменные 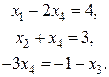 Запишем полученную систему в матричном виде: 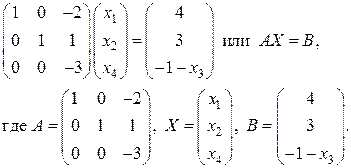 Ее решение 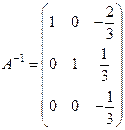 Поэтому 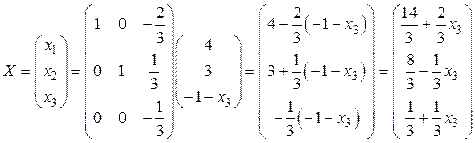 Сделав проверку, выпишем вид решения при втором способе выбора базиса: 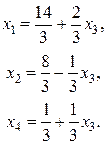 Чтобы найти вид решения при базисных переменных 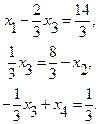 или или 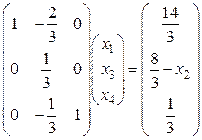 . .Решая аналогично предыдущему шагу, находим 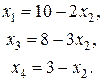 Наконец, выбираем в качестве базисных неизвестные Преобразуем предыдущее решение: 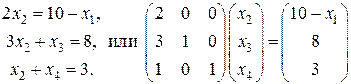 . .Решая выписанное матричное уравнение, найдем 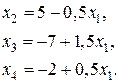 |
