Теория информации. Вариант_05. Выясните, какие из представленных ниже кодов, является префиксными
 Скачать 36.72 Kb. Скачать 36.72 Kb.
|
|
Выясните, какие из представленных ниже кодов, является префиксными: {01, 101, 110, 1, 10} {11, 001, 101, 1001, 110} { 10, 01, 110, 111} {01, 101, 110, 111} {11, 01, 011, 111} {01, 110, 001, 111} Ответ: префиксными кодами являются: {01, 101, 110, 1, 10} {10, 01, 110, 111} {01, 101, 110, 111} {01, 110, 001, 111} Дискретная случайная величина X, задана распределением:
Найти энтропию. Ответ: H(X) = - (0,15 * log2(0,15) + 0,2 * log2(0,2) + 0,1 * log2(0,1) + 0,15 * log2(0,15) + 0,1 * log2(0,1) + 0,05 * log2(0,05) + 0,2 * log2(0,2) + 0,05 * log2(0,05)) H(X) ≈ - (0,15 * (-3,16993) + 0,2 * (-2,32193) + 0,1 * (-3,32193) + 0,15 * (-3,16993) + 0,1 * (-3,32193) + 0,05 * (-4,32193) + 0,2 * (-2,32193) + 0,05 * (-4,32193)) H(X) ≈ 0,55354 + 0,46439 + 0,33219 + 0,47549 + 0,33219 + 0,21610 + 0,46439 + 0,21610 H(X) ≈ 2,25449 Энтропия дискретной случайной величины X составляет примерно 2,25449. Определить энтропию, приходящуюся в среднем на одну букву и на одно двухбуквенное сочетание, количество информации, которое несёт в себе сообщение о получении первой буквы относительно второй. В качестве сообщения использовать Ваше ФИО с пробелами, например: «Иванов Иван Иванович». Ответ: Сообщение: Лихобабин Василий Васильевич
Расчёт энтропии на основе вероятностей: H(буква) = - ((1/21) * log2(1/21) + (3/21) * log2(3/21) + (1/21) * log2(1/21) + (2/21) * log2(2/21) + (2/21) * log2(2/21) + (2/21) * log2(2/21) + (1/21) * log2(1/21) + (1/21) * log2(1/21) + (2/21) * log2(2/21) + (2/21) * log2(2/21) + (2/21) * log2(2/21) + (1/21) * log2(1/21) + (1/21) * log2(1/21) + (1/21) * log2(1/21) + (1/21) * log2(1/21)) H(буква) = - ((1/21) * (-4.39) + (3/21) * (-1.585) + (1/21) * (-4.39) + (2/21) * (-2.585) + (2/21) * (-2.585) + (2/21) * (-2.585) + (1/21) * (-4.39) + (1/21) * (-4.39) + (2/21) * (-2.585) + (2/21) * (-2.585) + (2/21) * (-2.585) + (1/21) * (-4.39) + (1/21) * (-4.39) + (1/21) * (-4.39) + (1/21) * (-4.39))) H(буква) = 0.202 + 0.227 + 0.202 + 0.393 + 0.393 + 0.393 + 0.202 + 0.202 + 0.393 + 0.393 + 0.393 + 0.202 + 0.202 + 0.202 + 0.202 H(буква) = 4.629 "Лихобабин Василий Васильевич" энтропия, приходящаяся в среднем на одну букву в сообщении составляет примерно 4.629 бит.
H(пара) = - ((1/21) * log2(1/21) + (1/21) * log2(1/21) + (1/21) * log2(1/21) + (2/21) * log2(2/21) + (1/21) * log2(1/21) + (1/21) * log2(1/21) + (1/21) * log2(1/21) + (1/21) * log2(1/21) + (1/21) * log2(1/21) + (1/21) * log2(1/21) + (1/21) * log2(1/21) + (1/21) * log2(1/21) + (1/21) * log2(1/21) + (1/21) * log2(1/21) + (1/21) * log2(1/21) + (1/21) * log2(1/21) + (1/21) * log2(1/21) + (1/21) * log2(1/21) + (1/21) * log2(1/21) + (1/21) * log2(1/21)) H(пара) = - ((1/21) * (-4.39) + (1/21) * (-4.39) + (1/21) * (-4.39) + (2/21) * (-2.585) + (1/21) * (-4.39) + (1/21) * (-4.39) + (1/21) * (-4.39) + (1/21) * (-4.39) + (1/21) * (-4.39) + (1/21) * (-4.39) + (1/21) * (-4.39) + (1/21) * (-4.39) + (1/21) * (-4.39) + (1/21) * (-4.39) + (1/21) * (-4.39) + (1/21) * (-4.39) + (1/21) * (-4.39) + (1/21) * (-4.39) + (1/21) * (-4.39) + (1/21) * (-4.39))) H(пара) = 0.202 + 0.202 + 0.202 + 0.393 + 0.202 + 0.202 + 0.202 + 0.202 + 0.202 + 0.202 + 0.202 + 0.202 + 0.202 + 0.202 + 0.202 + 0.202 + 0.202 + 0.202 + 0.202 + 0.202 H(пара) = 4.058 Энтропия, приходящаяся в среднем на одно двухбуквенное сочетание в сообщении "Лихобабин Василий Васильевич" составляет примерно 4.058 бит Ответ: Вероятности появления символов источника заданы таблицей:
Найти длину кода и информационную избыточность при равномерном кодировании. Ответ: Длина кода для каждого символа: L(1) = log2(1/(5/19)) L(2) = log2(1/(4/19)) L(3) = log2(1/(4/19)) L(4) = log2(1/(3/19)) L(5) = log2(1/(3/19)) L(1) = log2(19/5) L(2) = log2(19/4) L(3) = log2(19/4) L(4) = log2(19/3) L(5) = log2(19/3) I = (5/19) * L(1) + (4/19) * L(2) + (4/19) * L(3) + (3/19) * L(4) + (3/19) * L(5) I = (5/19) * log2(19/5) + (4/19) * log2(19/4) + (4/19) * log2(19/4) + (3/19) * log2(19/3) + (3/19) * log2(19/3) Длина кодов и информационная избыточность: L(1) ≈ 1.080 L(2) ≈ 1.292 L(3) ≈ 1.292 L(4) ≈ 1.585 L(5) ≈ 1.585 I ≈ 0.378 Таким образом, длины кодов при равномерном кодировании составляют около 1.080, 1.292, 1.292, 1.585 и 1.585 соответственно, а информационная избыточность составляет примерно 0.378. Используя частотные таблицы, полученные в задаче №3 и алгоритм Хаффмена, построить кодовые последовательности для букв русского алфавита. Каждый этап алгоритма необходимо подробно расписать. Используя частотные таблицы, полученные в задаче №3 и алгоритм Шеннона-Фано, построить кодовые последовательности для букв русского алфавита. Каждый этап алгоритма необходимо подробно расписать. Рассчитать среднюю длину кода для кодов, полученных в задачах №5 и №6. Определить, какой код наиболее эффективен. Методом взвешенных кодов закодировать и раскодировать сообщение «TEXT 123». TEXT заменить своим именем, 123 – количество букв в Вашем ФИО. Например для Иванов Иван Иванович получим: «IVAN 10» Используемый алфавит: Латинские буквы (A B C D E F G H I J K L M N O P Q R S T U V W X Y Z); цифры (1 2 3 4 5 6 7 8 9 0); знак пробела. Ответ: Присвоим каждому символу следующие веса: A = 10, B = 11, C = 12, D = 13, E = 14, F = 15, G = 16, H = 17, I = 18, J = 19, K = 20, L = 21, M = 22, N = 23, O = 24, P = 25, Q = 26, R = 27, S = 28, T = 29, U = 30, V = 31, W = 32, X = 33, Y = 34, Z = 35, пробел = 36, 1 = 1, 2 = 2, 3 = 3, 4 = 4, 5 = 5, 6 = 6, 7 = 7, 8 = 8, 9 = 9, 0 = 0. Теперь закодируем сообщение "VASILIY 20" с помощью взвешенных кодов: V = 31 (вес = 6) A = 10 (вес = 5) S = 28 (вес = 4) I = 18 (вес = 3) L = 21 (вес = 2) I = 18 (вес = 1) Y = 34 (вес = 0) (пробел) = 36 (вес = 0) 2 = 2 (вес = 0) 0 = 0 (вес = 0) Вычисление суммы взвешенных значений символов: 316 + 105 + 284 + 183 + 212 + 181 + 340 + 360 + 20 + 00 = 186 Контрольный символ (КС): КС = (37 - (186 % 37)) % 37 КС = (37 - 22) % 37 КС = 15 Закодированное сообщение "VASILIY 20" будет выглядеть как "V6A5S4I3L2I1Y0P". Раскодирование сообщения V = 31 (вес = 6) 6 = 6 (вес = 5) A = 10 (вес = 4) 5 = 5 (вес = 3) S = 28 (вес = 2) 4 = 4 (вес = 1) I = 18 (вес = 0) 3 = 3 (вес = 0) L = 21 (вес = 0) 2 = 2 (вес = 0) I = 18 (вес = 0) 1 = 1 (вес = 0) Y = 34 (вес = 0) 0 = 0 (вес = 0) P = 25 (вес = 0) Вычислим сумму взвешенных значений символов: 316 + 65 + 104 + 53 + 282 + 41 + 180 + 30 + 210 + 20 + 180 + 10 + 340 + 00 + 25*0 = 666 Проверим остаток от деления суммы на 37: 666 % 37 = 15 Методом Хемминга была закодировано некоторая комбинация α. После передачи по каналу связи было получено сообщение, содержащее комбинацию β =1100010. Необходимо проверить, есть ли ошибка в полученном сообщении и, при необходимости, исправить ее. Для решения использовать проверочную матрицу H и порождающую матрицу G: 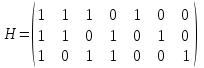 , , 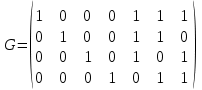 Ответ: β = 1100010 H^T = (1 1 1) (0 1 0) (1 0 1) (0 1 1) (1 0 0) (0 1 0) (0 0 1) Выполним операцию умножения по модулю 2: синдром = β * H^T = (1 1 1 0 1 0 0) * (1 1 1) = (0 0 0) Полученный синдром ошибки равен нулевому вектору (синдром = 000), что означает, что ошибки в полученном сообщении β нет. Исправление ошибки (если была бы обнаружена): В случае, если синдром ошибки не равен нулевому вектору, мы могли бы определить позицию ошибки, сравнивая синдром ошибки со столбцами проверочной матрицы H. Затем мы могли бы инвертировать бит в этой позиции в полученном сообщении β для исправления ошибки. Однако, поскольку синдром равен нулю, исправление ошибки не требуется. Таким образом, в полученном сообщении β = 1100010 ошибок нет и оно может быть рассматриваться как корректное. Методом Хемминга закодировать комбинацию α=0110, построить порождающую проверочную матрицу. Внести ошибку в один из разрядов кодового вектора, найти синдром, найти и исправить ошибку. 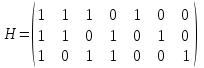 , , 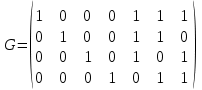 α = 0110 G = (1 0 0 0 1 1 1) (0 1 0 0 1 1 0) (0 0 1 0 1 0 1) (0 0 0 1 0 1 1) β = α * G = (0 1 1 0 0 0 0) Таким образом, полученный кодовый вектор β равен 0110000. Внесение ошибки: Изменяем один из разрядов кодового вектора, чтобы создать ошибку. Допустим, мы внесли ошибку, инвертируя третий разряд кодового вектора β. Тогда новый кодовый вектор β' будет: β' = 0100000 Нахождение синдрома: Умножаем полученный кодовый вектор β' на проверочную матрицу H, используя операцию умножения по модулю 2 (XOR), для вычисления синдрома ошибки. Синдром ошибки вычисляется следующим образом: синдром = β' * H^T, где H^T - транспонированная матрица H. Выполним необходимые вычисления: H^T = (1 1 1) (0 1 0) (1 0 1) (0 1 1) (1 0 0) (0 1 0) (0 0 1) синдром = β' * H^T = (0 1 0 0 0 0 0) * (1 1 1) = (1 1 1) Полученный синдром ошибки равен (1 1 1). Исправление ошибки: Сравниваем синдром ошибки со столбцами проверочной матрицы H, чтобы определить позицию ошибки. Инвертируем бит в позиции ошибки в кодовом векторе β' для исправления ошибки. В данном случае, синдром ошибки (1 1 1) указывает на третью позицию ошибки в проверочной матрице H. Мы инвертируем бит в третьей позиции кодового вектора β': Исправленный кодовый вектор β'' будет: β'' = 0110000 Таким образом, исправленный кодовый вектор β'' равен 0110000. Кодовый вектор β'' снова стал исходной комбинацией α=0110, что указывает на успешное исправление ошибки. |
