Астрономия 4-5. Астрономия задание 4-5. Вкгу им. Аманжолова Преподаватель Иманжанова Кульбарчин Тлеукановна Студен
 Скачать 133.22 Kb. Скачать 133.22 Kb.
|
|
ВКГУ им.Аманжолова Преподаватель: Иманжанова Кульбарчин Тлеукановна Студен: Удалов К.О. Группа: 2КФ-И Задание №4-5 1. Свободная энергия 2.Энтропия 3.Энтальпия 4.1 закон термодинамики 1. Свободная энергия Термодинамическая свободная энергия - это концепция, используемая в термодинамике химических или тепловых процессов в технике и науке. Изменение свободной энергии - это максимальный объем работы, который термодинамическая система может выполнить в процессе при постоянной температуре, и его знак указывает, является ли процесс термодинамически благоприятным или запрещенным. Поскольку свободная энергия обычно содержит потенциальную энергию, она не является абсолютной, а зависит от выбора нулевой точки. Следовательно, физически значимыми являются только относительные значения свободной энергии или изменения свободной энергии. Свободная энергия - это термодинамическая функция состояния, такая же, как внутренняя энергия, энтальпия и энтропия. Свободная энергия - это часть любой энергии первого закона, которая доступна для выполнения термодинамической работы при постоянной температуре, то есть работы, опосредованной тепловой энергией. Свободная энергия подвергается необратимой потере в ходе такой работы. Поскольку энергия первого закона всегда сохраняется, очевидно, что свободная энергия является расходуемым видом энергии второго закона. Несколько функций свободной энергии могут быть сформулированы на основе системных критериев. Функции свободной энергии представляют собой преобразования Лежандра внутренней энергии. Свободная энергия Гиббса определяется как G = H − TS, где H - энтальпия, T - абсолютная температура, а S - энтропия. H = U + pV, где U - внутренняя энергия, p - давление, а V - объем. G является наиболее полезным для процессов, включающих систему при постоянном давлении p и температуре T, потому что, в дополнение к включению любого изменения энтропии, вызванного просто нагревом, изменение G также исключает работу PD, необходимую для "освобождения места для дополнительных молекул", образующихся в результате различных процессов. Следовательно, изменение свободной энергии Гиббса равно работе, не связанной с расширением или сжатием системы, при постоянной температуре и давлении. (Отсюда его полезность для химиков, работающих в растворной фазе, включая биохимиков.) Исторически более ранняя свободная энергия Гельмгольца, напротив, определяется как A = U − TS. Ее изменение равно количеству обратимой работы, выполняемой или получаемой из системы при постоянном T. Отсюда его название "содержание работы" и обозначение A от Arbeit, немецкого слова, обозначающего работу. Поскольку она не ссылается на какие-либо величины, участвующие в работе (такие как p и V), функция Гельмгольца является полностью общей: ее уменьшение - это максимальный объем работы, который может быть выполнен системой при постоянной температуре, и он может увеличиваться максимум на объем работы, выполняемой в системеизотермически. Свободная энергия Гельмгольца имеет особое теоретическое значение, поскольку она пропорциональна логарифму функции разделения для канонического ансамбля в статистической механике. (Отсюда его полезность для физиков; и для химиков и инженеров газовой фазы, которые не хотят игнорировать работу PD.) Исторически термин "свободная энергия" использовался для любого количества. В физике свободная энергия чаще всего относится к свободной энергии Гельмгольца, обозначаемой A (или F), в то время как в химии свободная энергия чаще всего относится к свободной энергии Гиббса. Значения двух свободных энергий обычно довольно схожи, и предполагаемая функция свободной энергии часто подразумевается в рукописях и презентациях. 2.Энтропия В классической термодинамике энтропия-это свойство термодинамической системы, которое выражает направление или результат спонтанных изменений в системе. Этот термин был введен Рудольфом Клаузиусом в середине девятнадцатого века от греческого слова τρoπή (трансформация), чтобы объяснить взаимосвязь внутренней энергии, которая доступна или недоступна для преобразований в виде тепла и работы. Энтропия – термодинамическая функция состояния, поэтому ее изменение не зависит от пути процесса, а определяется только начальным и конечным состояниями системы. Тогда S2-S1 = dS Физической смысл энтропии – это количество связанной энергии, которая отнесенная к одному градусу: В изолированных системах, направления течения самопроизвольных процессов определяется изменением энтропии. 3.Энтальпия Энтальпи́я, также тепловая функция и теплосодержание — термодинамический потенциал, характеризующий состояние системы в термодинамическом равновесии при выборе в качестве независимых переменных давления, энтропии и числа частиц. Проще говоря, энтальпия — это та энергия, которая доступна для преобразования в теплоту при определенных температуре и давлении. Определением этой величины служит тождество: H=U+PV Размерность энтальпии-Дж/моль. В химии чаще всего рассматривают изобарические процессы (P = const), и тепловой эффект в этом случае называют изменением энтальпии системы или энтальпией процесса: 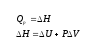 В термодинамической системе выделяющуюся теплоту химического процесса условились считать отрицательной (экзотермический процесс, ΔH < 0), а поглощение системой теплоты соответствует эндотермическому процессу, ΔH > 0. 4.1 закон термодинамики Первый закон термодинамики представляет собой некое обобщение закона сохранения и превращения энергии для термодинамической системы, и формулируется следующим образом: Определение 1 Изменение ΔU внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q, переданной системе, и работой A, совершенной системой над внешними телами. Формула первого закона термодинамики, зачастую записывается в ином виде: Определение 2 Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами. Первый закон термодинамики представляет из себя, по сути, обобщение опытных фактов. Если руководствоваться им, то можно заявить, что энергия не возникает и не исчезает бесследно, а передается от одной системы к другой, меняя свои формы. Невозможность создания вечного двигателя (perpetuum mobile) первого рода, то есть машины, которая может совершать полезную работу, не потребляя энергию извне и не претерпевая каких-либо изменений во внутренней конструкции агрегата, являлась важным следствием первого закона термодинамики. В подтверждение этого выступает тот факт, что каждая из огромного множества попыток создания такого устройства неизменно заканчивалась неудачей. Реальная машина может совершать положительную работу A над внешними объектами, только получая некоторое количество теплоты Q от окружающих тел или уменьшая ΔU своей внутренней энергии. Первый закон термодинамики в процессах газов Первый закон термодинамики может применяться к изопроцессам в газах. Определение 3 В изохорном процессе, то есть в условиях неизменного объема (V=const) газ не совершает работы, A=0. В этом случае справедливой будет формула внутренней энергии газа: В данном выражении U(T1) и U(T2) представляют внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит лишь от температуры, что исходит из закона Джоуля. При изохорном нагревании газ поглощает тепло (Q>0), чем провоцирует увеличение его внутренней энергии. В условиях охлаждения тепло отдается внешним объектам (Q<0). Определение 4 В изобарном процессе, предполагающем постоянность значения давления (p=const), работа, совершаемая газом, выражается в виде соотношения: A=p(V2−V1)=pΔV. Первый закон термодинамики для изобарного процесса дает: Q=U(T2)−U(T1)+p(V2−V1)=ΔU+pΔV При изобарном расширении Q>0 тепло поглощается газом, и он совершает положительную работу. При изобарном сжатии Q<0 тепло переходит внешним телам. В таком случае A<0A<0. При изобарном сжатии уменьшаются температура газа T2 Определение 5 В изотермическом процессе температура газа не меняет своей величины, следовательно, не изменяется и внутренняя энергия газа, ΔU=0. Первый закон термодинамики для изотермического процесса выражается соотношением Q=A Теплота Q, приобретенная газом в процессе изотермического расширения, превращается в работу, совершаемую над внешними объектами. И наоборот, изотермическое сжатие приводит к преобразованию уже работы внешних сил, произведенной над газом, в передающееся окружающим телам тепло. Вместе с изохорным, изотермическим и изобарным процессами в термодинамике нередко исследуют процессы, происходящие в условиях отсутствующего теплообмена с окружающими объектами. Определение 6 Адиабатическая оболочка – это сосуд с теплонепроницаемыми стенками. Определение 7 Процессы сжатия или расширения газа в подобных емкостях называют адиабатическими. 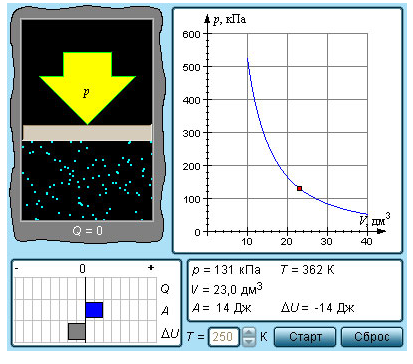 Рисунок – 1. Модель адиабатического процесса. Определение 8 В адиабатическом процессе Q=0. По данной причине первый закон термодинамики принимает вид: A=–ΔU. Выходит, что газ производит работу за счет падения значения его внутренней энергии. Определение 9 Расширение или сжатие газа на плоскости p, V проиллюстрирована кривой, называемой адиабатой. В процессе адиабатического расширения газом совершается положительная работа A>0, что является причиной понижения значения внутренней энергии ΔU<0. Данное явление провоцирует падение его температуры. Исходя из этого, можно заявить, что величина давления газа при адиабатическом расширении понижается быстрее, чем это происходит в изотермическом (рис. 2). 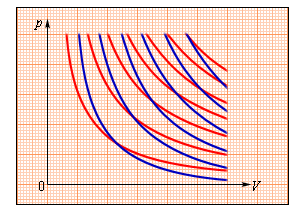 Рисунок – 2. Семейства изотерм (красные кривые) и адиабат (синие кривые) идеального газа В условиях координат (p, V)(p, V) выводящееся в термодинамике уравнение адиабатического процесса для идеального газа принимает следующий вид: pVγ=const. Работа газа в адиабатическом процессе выражается через температуры начального T1 и конечного T2 состояний и принимает вид: A=CV(T2−T1) Адиабатический процесс относится к изопроцессам. В термодинамике важное место занимает физическая величина, называемая энтропией. Изменение энтропии в том или ином квазистатическом процессе эквивалентно некоторому обретенному системой теплу ΔQT. Так как на каждом участке адиабатического процесса ΔQ=0, энтропия в нем не претерпевает изменений. Любые изопроцессы, в том числе и адиабатические, являются квазистатическими. Промежуточные состояния газа в таких процессах близки к состояниям термодинамического равновесия. Каждая точка, принадлежащая адиабате, описывает равновесное состояние. Однако, процесс, который проводится в адиабатической оболочке, то есть при отсутствующем теплообмене с окружающими объектами, не обязательно удовлетворяет данному условию. |
