Влгу курсовая работа по дисциплине Методология научных исследований Тема Деформирование стержня поперечной нагрузкой
 Скачать 83.5 Kb. Скачать 83.5 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых» (ВлГУ) КУРСОВАЯ РАБОТА по дисциплине: Методология научных исследований Тема: Деформирование стержня поперечной нагрузкой
Владимир 2020 Задание Балка длиной ℓ=3,0 м имеет поперечное сечение в виде прямоугольника с размерами в×h =200×400 мм, шарнирно опирается по концам и нагружена двумя сосредоточенными силами F=5,0 МН, как показано на рисунке 1. Модуль упругости материала Е =2,06∙105 МПа, коэффициент Пуассона µ=0,25. 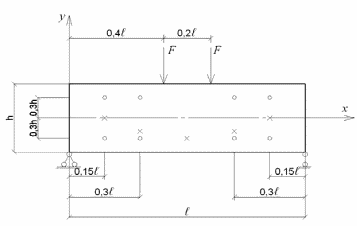 Рисунок 1 – Схема балки. ○ – точки А, × - точки В,С,D,E,F. Требуется: 1. Для точки А с координатами (0,85ℓ; 0,3h), определить нормальные и касательные напряжения, действующие в следующих площадках: а) перпендикулярных координатным осям x,y, б) имеющих наклон к оси x 450 и 1350, в) главных площадках – напряжения σmax, σmin. Определить деформации ε в направлениях, перпендикулярных этим площадкам. Представить площадки с напряжениями и деформациями на рисунках, причем длины векторов, указывающих напряжения или деформации должны быть пропорциональны численному значению величин. 2. Для точек B,C,D,E,F с координатами: В(0,15ℓ; 0), С(0,30ℓ; -0,2h), D(0,5ℓ; -0,30h), Е(0,7ℓ; -0,2h), F(0,85ℓ; 0) определить главное напряжение σmax и площадку его действия. Показать их на рисунке балки. Приближенно провести траекторию главных напряжений – кривую, касательная к которой в любой точке совпадает с направлением действия напряжения σmax. 3. Описать словами деформирование балки. Решение: Координаты точек: т. А (2,55; 0,12) т. В (0,45; 0) т. С (0,9; -0,08) т. D (1,5; -0,12) т. E (2,1; -0,08) т. F (2,55; 0) Построим эпюру моментов для балки с заданной нагрузкой Сумма моментов всех сил относительно точки 1 должна равняться нулю: Сумма моментов всех сил относительно точки 2 должна равняться нулю: Для проверки вычислим сумму проекций всех сил на вертикальную ось: Реакции опор найдены верно. Составим аналитические выражения Q(z) и M(z) для каждого участка и вычислим их значения в характерных точках. Участок I (0 ≤ z ≤ 1,2): Поперечная сила QI (z) = RA = 5; Значения Q на краях отрезка: QI(0) = 5 МН; QI(1,2) = 5 МН. Изгибающий момент M: MI(z) = RA z = 5∙z; Значения M на краях отрезка: MI(0) = 5·0 = 0 МН∙м; MI(1,7) = 5·1,2 = 6 МН∙м; Участок II (1,2 ≤ z ≤ 1,8): Поперечная сила QII (z) = RA – F1 = 5 - 5 = 0; Значения Q на краях отрезка: QII (1,2) = 0 МН; QII (1,8) = 0 МН. Изгибающий момент M: MII(z) = RA z - F1(z - c1)= = 5z - 5(z – 1,2)= 6 МН∙м; Значения M на краях отрезка: MII (1,2) = 6 МН∙м; MII (1,8) = 6 МН∙м; Участок III (1,8 ≤ z ≤ 3,0): Поперечная сила QIII (z) = RA – F1 – F2= 5 – 5 – 5 = -5; Значения Q на краях отрезка: QIII (1,8) = -5 МН; QIII (3,0) = -5 МН. Изгибающий момент M: MIII (z) = RA z – F1(z - c1) – F2(z – c2)= 5∙z –5(z –1,2) – - 5(z – 1,8) = -5∙z – 15; Значения M на краях отрезка: MIII (1,8) = -5·1,8 + 15 = 6 МН∙м; MIII (3,0) = -5·3 + 15 = 0 МН∙м; Исследование напряженно-деформированного состояния в точке А Точка А находится в верхней, сжатой части сечения. Геометрические характеристики сечения 2.1 Определение нормальных напряжений в т. А, действующих в перпендикулярных площадках к координатным осям Х и Y. Найдем σх в т.А по формуле: σy = 0, т.к. принята гипотеза о не надавливании продольных волокон друг на друга, т.е. каждое продольное волокно находится в условиях центрального растяжения-сжатия. Определим касательные напряжения в точке А, действующие в перпендикулярных площадках к координатным осям X и Y по формуле Журавского: 2.2 Определение нормальных напряжений в т. А, действующих в площадках, имеющих наклон к оси Х 450 и 1350. При ⍺=450 При ⍺=1350 2.3. Определение нормальных и касательных напряжений в главных площадках σmax и σmin Определим нормальные и касательные напряжения в главных площадках σmax и σmin по формуле: Определение главных площадок Определим главные площадки 2⍺ = -25,360 ⍺ = -12,680 Определение деформаций ξ Принятые гипотезы позволяют считать, что при изгибе продольные волокна балки испытывают центральное растяжение или сжатие в направлении оси Х. При идеально упругом материале продольная деформация в этом случае определяется по закону Гука: где Е – модуль упругости материала. При этом возникает и поперечная деформация. Она противоположна продольной по знаку, и ее величина определяется коэффициентом Пуассона μ: Определим деформации: а) в площадках, перпендикулярных к оси X и Y б) в наклонных площадках при ⍺=450 при ⍺=1350 в) в главных площадках Исследование напряженно-деформированного состояния в точках B,C,D,E,F Для точек B,C,D,E,F с координатами: В(0,45; 0), С(0,9; -0,08), D(1,5; -0,12), Е(2,1; -0,08), F(2,55; 0) определим главное напряжение σmax и площадку его действия. Покажем их на рисунке балки. Приближенно проведем траекторию главных напряжений – кривую, касательная к которой в любой точке совпадает с направлением действия напряжения σmax. 3.1. Расчеты для точки В (0,45; 0) σy = 0, т.к. принята гипотеза о не надавливании продольных волокон друг на друга, т.е. каждое продольное волокно находится в условиях центрального растяжения-сжатия. Определим касательные напряжения в точке B, действующие в перпендикулярных площадках к координатным осям X и Y по формуле Журавского: Определяем главное напряжение σmax и площадку его действия 2⍺ = 900 ⍺ = 450 3.2. Расчеты для точки С (0,9; -0,08) σy = 0, т.к. принята гипотеза о не надавливании продольных волокон друг на друга, т.е. каждое продольное волокно находится в условиях центрального растяжения-сжатия. Определим касательные напряжения в точке C, действующие в перпендикулярных площадках к координатным осям X и Y по формуле Журавского: Определяем главное напряжение σmax и площадку его действия 2⍺ = -24,940 ⍺ = -12,470 3.3. Расчеты для точки D (1,5; -0,12) σy = 0, т.к. принята гипотеза о не надавливании продольных волокон друг на друга, т.е. каждое продольное волокно находится в условиях центрального растяжения-сжатия. Определим касательные напряжения в точке D, действующие в перпендикулярных площадках к координатным осям X и Y по формуле Журавского: т.к. согласно эпюре Qy в точке D напряжение равно 0. Определяем главное напряжение σmax и площадку его действия 2⍺ = 1800 ⍺ = 900 3.4. Расчеты для точки E (2,1; -0,08) σy = 0, т.к. принята гипотеза о не надавливании продольных волокон друг на друга, т.е. каждое продольное волокно находится в условиях центрального растяжения-сжатия. Определим касательные напряжения в точке E, действующие в перпендикулярных площадках к координатным осям X и Y по формуле Журавского: Определяем главное напряжение σmax и площадку его действия 2⍺ = 24,940 ⍺ = 12,470 3.5. Расчеты для точки F (2,55; 0) σy = 0, т.к. принята гипотеза о не надавливании продольных волокон друг на друга, т.е. каждое продольное волокно находится в условиях центрального растяжения-сжатия. Определим касательные напряжения в точке F, действующие в перпендикулярных площадках к координатным осям X и Y по формуле Журавского: Определяем главное напряжение σmax и площадку его действия 2⍺ = -900 ⍺ = -450 Траектория главных напряжений для точек В, C, D, E, F Представим на рисунке направление действия главных напряжений и поворот главных площадок в т. В, C, D, E, F  Деформирование балки при чистом изгибе При чистом изгибе происходит деформирование балки. Верхние волокна укорачиваются, а нижние удлиняются. При действии двух сосредоточенных сил на балку главные площадки точек, расположенных на удалении от нейтральной линии поворачиваются на угол ⍺ = -12,680 (найден по расчету). Главные площадки точек, расположенных на нейтральной линии балки остаются на своих местах ⍺ = 00. Если провести касательную к вектору лавных напряжений, действующих в обозначенных точках балки, то можно увидеть, что эта линия симметрична относительно оси Y и имеет параболические очертания (очертания изгиба балки). В точке А в главных площадках деформирование ξmax= 38,91∙10-5 м; ξmin= -131,06∙10-5 м. Заключение На балку длиной 3 м, имеющую поперечное сечение в виде прямоугольника b×h 200×400 мм, шарнирно опирающуюся по концам, действуют две сосредоточенные силы по 5 МН, в результате чего образуется деформация. В ходе курсовой работы были определены нормальные и касательные напряжения, действующие на площадках, перпендикулярных к осям X и Y, в площадках, имеющих наклон к оси X 450 и 1350, а также в действующих в главных площадках в т. А. Так же были определены деформации в направлении, перпендикулярном этим площадкам. Для точек В, C, D, E, F также были определены главные напряжения σmax и площадки их действия, показанные на рисунках к балке, проведена траектория главных напряжений, кривая, касательная к которой в любой точке совпадает с направлением действия напряжения σmax. При деформации балки образуется изгиб. При исследовании деформирования балки принимаются следующие гипотезы: - гипотеза плоских сечений – при деформировании балки ее поперечные сечения остаются плоскими; - гипотеза о не надавливании продольных волокон друг на друга; - материал балки принимается идеально упругим. Список используемой литературы: Научно-исследовательские работы (курсовые, дипломные, диссертации): общая методология, методика подготовки и оформления [Электронный ресурс]: Учебное пособие / Алексеев Ю.В., Казачинский В.П., Никитина Н.С.: Издательство АСВ, 2012. – 120 с. Промышленное и гражданское строительство в задачах с решениями [Электронный курс] / Красновский Б.М. – Издание 2 – е, доп. – М.: Издательство АСВ, 2015. – 1432 с. Задания и методические указания к выполнению расчетно-графической работы: «Расчет балки на прочность и жесткость» / Сост. С.В. Гусев, Казань: КГАСУ, 2011. – 25 с. Метод конечных элементов в решении задач механики несущих систем. [Электронный ресурс]: Учебное пособие / Серпик И.Н. – М.: Издательство АСВ, 2014. – 200 с. |
