Влияние нанокремнезема на прочность высокопрочных легких бетонов для жилищного строительства

• Название: Влияние нанокремнезема на прочность высокопрочных легких бетонов для жилищного строительства
• Дата: 22.05.2021
• Размер: 391.13 Kb.
• Имя файла: Primer_vypolnenia_domashnego_zadania.docx
• Тип: Отчет; #208538
• страница: 4 из 6

2.1. Методы исследований, приборы и оборудование

Определение предела прочности при сжатии образцов бетона осуществляется по ГОСТ 10180-90. «Бетоны. Методы определения прочности по контрольным образцам» на 1 сутки после ТВО и 28 сутки естественного твердения на образцах 70×70×70 мм. Для испытания может использоваться прессовое оборудование, обеспечивающее статическое нагружение со скоростью согласно ГОСТ.

3. ДЕКОМПОЗИЦИЯ ИССЛЕДУЕМОЙ СИСТЕМЫ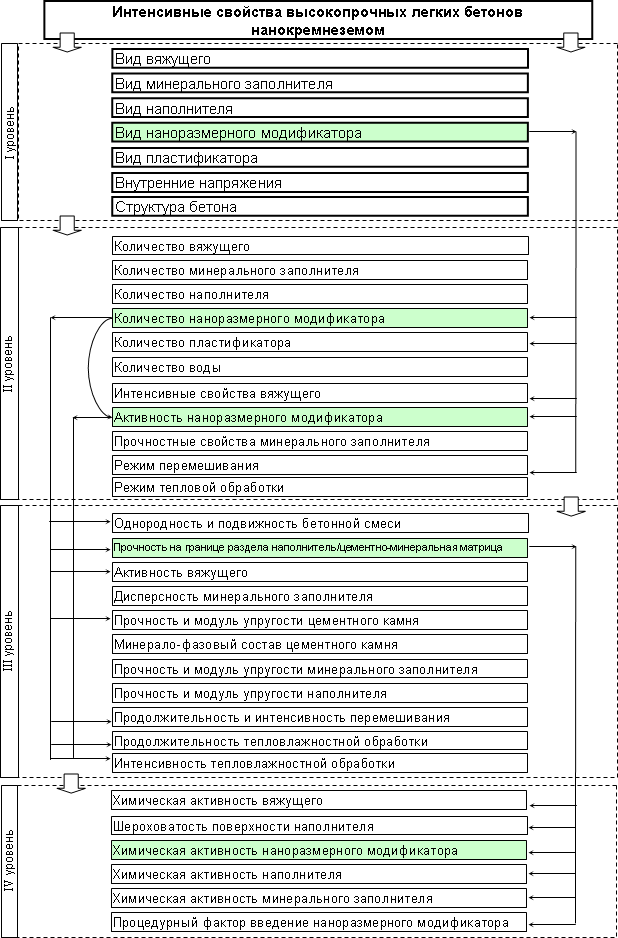

В соответствии с выбранной тематикой и определенным объектом исследования (высокопрочным легким бетоном) и предметом исследования (влияние наномодификатора на прочностные свойства) выполним декомпозицию критериев качества до элементарных фрагментов (рисунок 4).

Рисунок 4 – Декомпозиция интенсивных свойств наномодифицированных высокопрочных легких бетонов

Таким образом, из множества взаимозависящих факторов, оказывающих, в том числе, влияние на прочностные свойства исследуемого объекта, в соответствии с рассматриваемым предметом исследования выполнена декомпозиция интенсивных свойств по 4 уровням и выделены элементарные факторы. Изменяя количество нанокремнезема в объеме бетона при постоянной его концентрации, можно обеспечить изменение предела прочности при сжатии за счет управления прочностью на границе раздела фаз. То есть количественным критерием для оценки влияния нанокремнезема является предел прочности при сжатии, а управляющим фактором – количество нанокремнезема.

4. ПЛАНИРОВАНИЕ И ОБРАБОТКА ЭКСПЕРИМЕНТА

На основе установленных в разделе 3 количественного критерия и управляющего фактора смоделируем результаты эксперимента. Пусть x– количество нанокремнезема (C_д), y– прочность при сжатии (R_сж).

В результате эксперимента получена следующая зависимость этих параметров:

Параметр	Номер эксперимента
	1	2	3	4	5
Фактор xi	3	12	27	44	50
Критерий yi	-3,2	1	6,4	8	9,6
Примечания: Ц1, Ц2 Ц3 и Ц4 – Первая, вторая, предпоследняя и последняя цифра номера зачетной книжки, соответственно

В соответствии с заданием проверим, является ли уравнение y = ax + bфункцией, достоверно описывающей имеющиеся экспериментальные данные.

Коэффициенты aи bфункции y= ax+ b найдём как решение системы:

^^a



x²  b_ x_i

 _ x_i y_i

i
_a_ x_i bn _ y_i

	1	2	3	4	5	∑
xi	3	12	27	44	50	136
yi	-3,2	1	6,4	8	9,6	21,8
xi2	9	144	729	1936	2500	5318
xiyi	-9,6	12	172,8	352	480	1007

Получим систему уравнений с 2-мя неизвестными:



^{5318a136b 1007}

_136a 5b 21,8 ^,

Решение методом Крамера:

_{ } 5318

136

136

5

 5318 5 136136  8094 _,

∆=8094≠0, значит система имеет единственное решение.

_{ } 1007

^a 28,8

136

5

 1007  5 136  21,8  2071,2

_b

5318

136

1007

21,8

 5318 21,8 1007 136  21046,8

Тогда a и b найдем как

a ^a



_ 2071,2

8094
 0,26

b ^b



_ 21046,8

8094
 2,60

Таким образом, получим уравнение y= 0,26x- 2,60

параметр bхарактеризует базовое (контрольное) значение контролируемого параметра без влияния управляемого фактора. Коэффициент aпоказывает интенсивность влияния фактора x, положительный знак которого свидетельствует о возрастающем направлении графика.

С учетом присвоенного физического смысла исходным математическим данным уравнение будет иметь следующий вид:

R_сж = 0,26C_д - 2,60 (1)

Выполняя анализ полученного уравнения можно, было бы сделать вывод, что полученные результаты исследования можно подвергнуть сомнению, так как отрицательные значения предела прочности при сжатии не имеют смысла.





Вычислим сумму квадратов отклонений между эмпирическими и теоретическими значения yот величины x.



e

i
² y_i

• 
  fx_i
  

²

	1	2	3	4	5	∑
xi	3	12	27	44	50	136
yi	-3,2	1	6,4	8	9,6	21,8
f(xi)	-1,83	0,47	4,31	8,66	10,19	–
(yi -f(xi))2	1,87	0,28	4,37	0,43	0,35	7,31

Полученная величина ∑e² = 7,31 свидетельствует о том, что линейная функция скорее является не наилучшей для аппроксимации исходных экспериментальных данных.

Используя специализированное программное обеспечение для

имеющихся экспериментальных данных может быть использована математическая модель

y ab e^cx

Со следующими эмпирическими коэффициентами a= 16,4686; b= 0,681202;

c= 0,0421648. Тогда уравнение примет вид

при ∑e² = 0,859.

^Rсж

 16,50,681 e^0,042Сд 
(2)

То есть вторая модель, лучшим образом аппроксимирует экспериментальные данные и может быть использована для прогнозирования контролируемых параметров от величина управляющего фактора.

Так при величине x=C_д = 10 значение г/м³ y= R_сж = 0,42 МПа, а при

x=C_д = 10 г/м³ y= R_сж = 5,48 МПа.


Предел прочности при сжатии, МПа
Построим график функций (рисунок 5)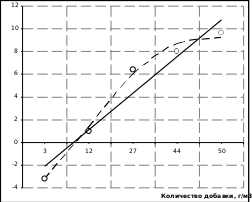

Рисунок 5 – График функций, аппроксимирующих экспериментальные данные (сплошная линия – уравнение 1, пунктирная – уравнение 2)