|
|
ВОЛС. Оптическое волокно Сандугаш. Волоконнооптические
1.1.3.З. Решения уравнений Максвелла Как уже отмечалось, всестороннее исследование характеристик ОВ может быть проведено только на основе волновой теории, путем решения уравнений Максвелла, которые для продольных составляющих электрического 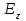 и магнитного и магнитного 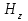 полей применительно к сердцевине двухслойного ОВ, ось которого совмещена с осью г цилиндрической системы координат, имеют вид полей применительно к сердцевине двухслойного ОВ, ось которого совмещена с осью г цилиндрической системы координат, имеют вид 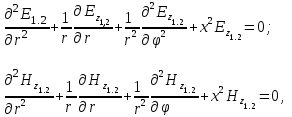 (1.41) (1.41)
где 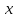 = = 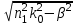 ‚ поперечный коэффициент распространения волны в сердцевине волокна: ‚ ‚ поперечный коэффициент распространения волны в сердцевине волокна: ‚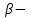 продольный коэффициент распространения; продольный коэффициент распространения; 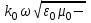 волновое число; волновое число; 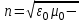 коэффициент преломления; коэффициент преломления; 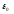 и и 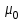 диэлектрическая и магнитная проницаемости среды, а индексы 1 и 2 соответствуют параметрам сердцевины и оболочки. диэлектрическая и магнитная проницаемости среды, а индексы 1 и 2 соответствуют параметрам сердцевины и оболочки.
Учитывая, что волокно выполняется из немагнитного материала, 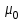 =1, а =1, а 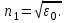 Как известно, в силу отличия физических процессов распространения волн в сердцевине и оболочке ОВ для решения данных систем уравнений используются различные функции. Так, для сердцевины решения ищутся в виде функций Бесселя и записываются как Как известно, в силу отличия физических процессов распространения волн в сердцевине и оболочке ОВ для решения данных систем уравнений используются различные функции. Так, для сердцевины решения ищутся в виде функций Бесселя и записываются как 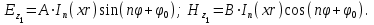 Решения уравнений для оболочки выражаются через функцию Ган- келя и имеют вид Решения уравнений для оболочки выражаются через функцию Ган- келя и имеют вид 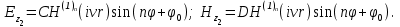 Поперечные составляющие векторов сердцевины и оболочки выражаются через комбинацию продольных составляющих Поперечные составляющие векторов сердцевины и оболочки выражаются через комбинацию продольных составляющих 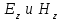 и при и при 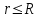 представляются в виде представляются в виде 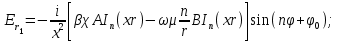 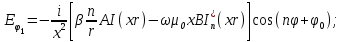 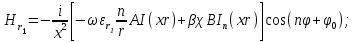 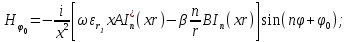 Соответственно при Соответственно при 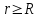 имеем имеем 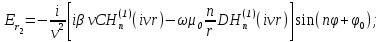 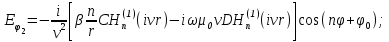 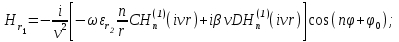 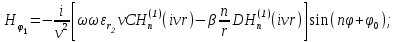 Постоянные интегрирования А, В, С, В в последних выражениях определяются из граничных условий на поверхности раздела сред при Постоянные интегрирования А, В, С, В в последних выражениях определяются из граничных условий на поверхности раздела сред при 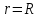 которые задаются как которые задаются как 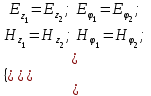 В результате имеет место следующая однородная система уравнений: В результате имеет место следующая однородная система уравнений: 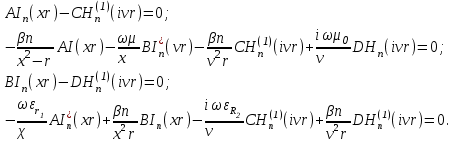 Приравнивая к нулю определитель полученной системы уравнений, решение ищется относительно д в виде так называемого основного дисперсионного уравнения [2]: Приравнивая к нулю определитель полученной системы уравнений, решение ищется относительно д в виде так называемого основного дисперсионного уравнения [2]: 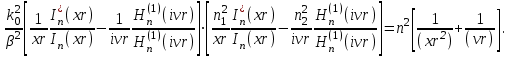 (1.42) Данное уравнение позволяет найти решение относительно (1.42) Данное уравнение позволяет найти решение относительно 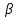 и рассчитать структуру поля в сердцевине и оболочке ОВ, зная значения поперечных коэффициентов распространения и рассчитать структуру поля в сердцевине и оболочке ОВ, зная значения поперечных коэффициентов распространения 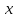 и и 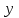 . В общем случае уравнения такого вида имеют ряд решений, каждому из которых соответствует определенный тип волны, называемый модой, которая определяется сложностью структуры поля, в частности числом максимумов и минимумов в поперечном сечении, и обозначается двумя числовыми индексами nи m. Индекс п означает число изменений поля по периметру ОВ, а индекс m - число изменений поля по диаметру. В оптическом волокне могут распространяться два типа волн: симметричные продольные . В общем случае уравнения такого вида имеют ряд решений, каждому из которых соответствует определенный тип волны, называемый модой, которая определяется сложностью структуры поля, в частности числом максимумов и минимумов в поперечном сечении, и обозначается двумя числовыми индексами nи m. Индекс п означает число изменений поля по периметру ОВ, а индекс m - число изменений поля по диаметру. В оптическом волокне могут распространяться два типа волн: симметричные продольные 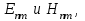 , у которых по одной продольной составляющей, и несимметричные волны, имеющие одновременно по две продольные составляющие, одна из которых , у которых по одной продольной составляющей, и несимметричные волны, имеющие одновременно по две продольные составляющие, одна из которых 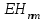 с преобладанием электрической составляющей Е: и другая НЕМ" с преобладанием магнитной составляющей Н. Следует отметить, что, связывая электромагнитную теорию с лучевой теорией, симметричные волны будут соответствовать меридианным лучам, а несимметричные — косым лучам. В случае симметричных мод, у которых поле не зависит от азиму- тального угла ф, правая часть дисперсионного уравнения равна нулю, и оно распадается на два уравнения: с преобладанием электрической составляющей Е: и другая НЕМ" с преобладанием магнитной составляющей Н. Следует отметить, что, связывая электромагнитную теорию с лучевой теорией, симметричные волны будут соответствовать меридианным лучам, а несимметричные — косым лучам. В случае симметричных мод, у которых поле не зависит от азиму- тального угла ф, правая часть дисперсионного уравнения равна нулю, и оно распадается на два уравнения: 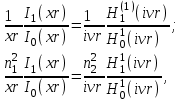 (1.43) первое из которых определяет характеристики составляющих направленных магнитных Н-мод, в которых (1.43) первое из которых определяет характеристики составляющих направленных магнитных Н-мод, в которых 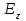 =0‚ =0‚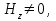 а второе -— электрических Е-мод с а второе -— электрических Е-мод с 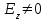 и и 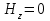 . Очевидно, что изменение значений . Очевидно, что изменение значений 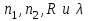 приводит к изменению числа решении данных дисперсионных уравнений и, следовательно, числа распространяющихся в волокне симметричных мод. 1.1.4. Нормированная и критическая частота Условием существования направляемой моды является экспоненциальное убывание ее поля в оболочке вдоль координаты r, причем степень уменьшения напряженности с ростом r определяется значением v, уменьшение которой приводит к перераспределению поля в оболочку ОВ – появлению вытекающих волн. При v=0 происходит качественное изменение волнового процесса, заключающегося в невозможности существования направляемой моды. Этот режим называется критическим, в связи с чем очень важно определение условий его возникновения, что можно осуществить подстановкой в последнее уравнение значения v=0, в результате правые части уравнений обращаются в бесконечность и для Е и Н мод будет справедливо условие приводит к изменению числа решении данных дисперсионных уравнений и, следовательно, числа распространяющихся в волокне симметричных мод. 1.1.4. Нормированная и критическая частота Условием существования направляемой моды является экспоненциальное убывание ее поля в оболочке вдоль координаты r, причем степень уменьшения напряженности с ростом r определяется значением v, уменьшение которой приводит к перераспределению поля в оболочку ОВ – появлению вытекающих волн. При v=0 происходит качественное изменение волнового процесса, заключающегося в невозможности существования направляемой моды. Этот режим называется критическим, в связи с чем очень важно определение условий его возникновения, что можно осуществить подстановкой в последнее уравнение значения v=0, в результате правые части уравнений обращаются в бесконечность и для Е и Н мод будет справедливо условие 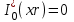 (1.44) которое определяет границы их возникновения или исчезновения. Последнее уравнение имеет бесчисленное множество решений, поэтому, обозначив положительный корень через (1.44) которое определяет границы их возникновения или исчезновения. Последнее уравнение имеет бесчисленное множество решений, поэтому, обозначив положительный корень через 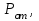 а также используя выражения для у и у, мы получаем а также используя выражения для у и у, мы получаем 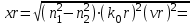 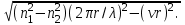 Введем величину, которая носит название нормированной частоты: Введем величину, которая носит название нормированной частоты: 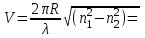 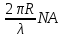 (1.45) Это один из важнейших обобщающих параметров, используемых для оценки свойств ОВ, который связывает его структурные параметры и длину световой волны аспространяемой в волокне. Тогда (1.45) Это один из важнейших обобщающих параметров, используемых для оценки свойств ОВ, который связывает его структурные параметры и длину световой волны аспространяемой в волокне. Тогда 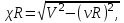 и при v=0 для каждого из корней имеет место критическое значение нормированной частоты: и при v=0 для каждого из корней имеет место критическое значение нормированной частоты: 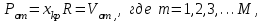 (1.46) A (1.46) A 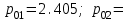 5.520; 5.520;  Если для некоторой симметричной моды нормированная частота больше ее критического значения Если для некоторой симметричной моды нормированная частота больше ее критического значения 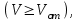 то она распространяется в ОВ, в противном случае ее нет. Так, при 2.4О5<У<5.52О в ОВ распространяются моды то она распространяется в ОВ, в противном случае ее нет. Так, при 2.4О5<У<5.52О в ОВ распространяются моды 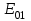 , и , и 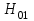 , а при 5.520<У<8.6`54 к ним добавляются моды Е”, Но, и т. д., в то время как неравенство У<2.4О5 указывает на отсутствие симметричных мод. Последняя формула позволяет определить значения критических длин волн , а при 5.520<У<8.6`54 к ним добавляются моды Е”, Но, и т. д., в то время как неравенство У<2.4О5 указывает на отсутствие симметричных мод. Последняя формула позволяет определить значения критических длин волн 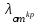 для симметричных волн в виде [2] для симметричных волн в виде [2]  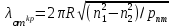  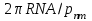 (1.47) или, переходя к частоте, (1.47) или, переходя к частоте, 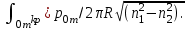 (1.48) Очевидно, что для распространяющейся моды должно выполняться условие ‚ (1.48) Очевидно, что для распространяющейся моды должно выполняться условие ‚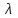 < <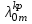 , т. е. , т. е. 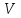 > >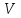 ‚ в противном случае этой моды нет. В отличие от симметричных мод несимметричные имеют все шесть составляющих векторов электромагнитного поля и их невозможно разделить на электрические и магнитные. Критическая нормирования частоте в этом случае определяется выражением ‚ в противном случае этой моды нет. В отличие от симметричных мод несимметричные имеют все шесть составляющих векторов электромагнитного поля и их невозможно разделить на электрические и магнитные. Критическая нормирования частоте в этом случае определяется выражением 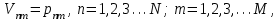 (1.49) В результате чего при заданных параметрах ОВ критическая длина волны равна (1.49) В результате чего при заданных параметрах ОВ критическая длина волны равна 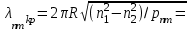 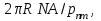 (1.50) где (1.50) где 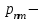 положительный корень соответствующего трансцендентного уравнения: положительный корень соответствующего трансцендентного уравнения: 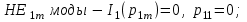 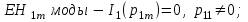 (1.51) (1.51) 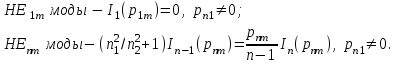 Указанные уравнения также получены из основного дисперсионного уравнения при v=0. Среди направляемых мод особое положение занимает мода НЕ11, у которой критическое значение нормированной частоты V11=0. Это основная (фундаментальная) мода ступенчатого ОВ, так как она распространяется при любой частоте и структурных параметрах волокна. С точки зрения геометрической оптики, она образуется лучом, вводимым вдоль оси волокна, так как только характеристики такого луча не зависят от условий отражения на границе “сердцевина — оболочка". Выбирая параметры ОВ, можно получить режим распространения только этой моды, что реализуется при условии Указанные уравнения также получены из основного дисперсионного уравнения при v=0. Среди направляемых мод особое положение занимает мода НЕ11, у которой критическое значение нормированной частоты V11=0. Это основная (фундаментальная) мода ступенчатого ОВ, так как она распространяется при любой частоте и структурных параметрах волокна. С точки зрения геометрической оптики, она образуется лучом, вводимым вдоль оси волокна, так как только характеристики такого луча не зависят от условий отражения на границе “сердцевина — оболочка". Выбирая параметры ОВ, можно получить режим распространения только этой моды, что реализуется при условии 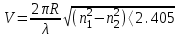 (152) Минимальная длина волны, при которой в волокне распространяется фундаментальная мода, называется волоконной длиной волны отсечки, значение которой легко определяется из последнего выражения как (152) Минимальная длина волны, при которой в волокне распространяется фундаментальная мода, называется волоконной длиной волны отсечки, значение которой легко определяется из последнего выражения как 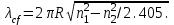 (1-53) Однако на практике больший интерес представляет так называемая кабельная длина волны отсечки (1-53) Однако на практике больший интерес представляет так называемая кабельная длина волны отсечки 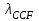 , которая смещена относительно , которая смещена относительно 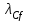 , в область более коротких волн из-за влияния механических напряжений, возникающих при укладке оптического волокна в кабель. Ввиду сложности теоретического учета влияния данных воздействий для определения , в область более коротких волн из-за влияния механических напряжений, возникающих при укладке оптического волокна в кабель. Ввиду сложности теоретического учета влияния данных воздействий для определения 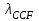 используется экспериментальные методы. При увеличении нормированной частоты в ОВ появляются другие моды, которые принято называть высшими. Каждая из этих мод обладает характерной для нее структурой электромагнитного поля в сердцевине и оболочке, а также запаздыванием по фазе используется экспериментальные методы. При увеличении нормированной частоты в ОВ появляются другие моды, которые принято называть высшими. Каждая из этих мод обладает характерной для нее структурой электромагнитного поля в сердцевине и оболочке, а также запаздыванием по фазе 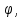 которое для симметричных и несимметричных мод определяется в результате численного решения соответствующих дисперсионных уравнений. На практике вместо дисперсионных характеристик которое для симметричных и несимметричных мод определяется в результате численного решения соответствующих дисперсионных уравнений. На практике вместо дисперсионных характеристик 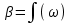 удобнее использовать нормированные дисперсионные параметры удобнее использовать нормированные дисперсионные параметры 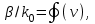 которые описывают свойства всех ступенчатых ОВ. Лучевая трактовка до иллюстрируется рис. 1.6, на котором показан процесс распространения меридианных лучей по двухслойному волокну. Здесь показаны предельные случаи распространения малых длин волн и волн, соизмеримых с диаметром сердцевины волокна. Рис. 1.6. Распространение излучения по ступенчатому волокну при различных частотах оптического излучения В первом случае, когда которые описывают свойства всех ступенчатых ОВ. Лучевая трактовка до иллюстрируется рис. 1.6, на котором показан процесс распространения меридианных лучей по двухслойному волокну. Здесь показаны предельные случаи распространения малых длин волн и волн, соизмеримых с диаметром сердцевины волокна. Рис. 1.6. Распространение излучения по ступенчатому волокну при различных частотах оптического излучения В первом случае, когда 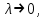 угол угол 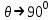 и, следовательно, волна стремится к более предпочтительному прямолинейному движению вдоль оси волокна, а во втором случае ‚ и, следовательно, волна стремится к более предпочтительному прямолинейному движению вдоль оси волокна, а во втором случае ‚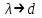 и и 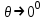 - волна претерпевает большое число отражений, в связи с чем значительно увеличивается длина пути оптического луча. При определенной длине волны наступает такой режим, при котором - волна претерпевает большое число отражений, в связи с чем значительно увеличивается длина пути оптического луча. При определенной длине волны наступает такой режим, при котором 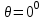 , и волна, падая на границу “сердцевина — оболочка”, отражается от нее под прямым углом. В этом случае в ОВ устанавливается режим стоячей волны, и энергия вдоль волокна не распространяется, что соответствует случаю критической длины волны. Поэтому по ОВ возможна передача электромагнитного излучения только с длиной волны, меньшей диаметра волокна, т. е. , и волна, падая на границу “сердцевина — оболочка”, отражается от нее под прямым углом. В этом случае в ОВ устанавливается режим стоячей волны, и энергия вдоль волокна не распространяется, что соответствует случаю критической длины волны. Поэтому по ОВ возможна передача электромагнитного излучения только с длиной волны, меньшей диаметра волокна, т. е. 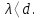 1.1.5. Число направляемых мод и длина волны отсечки Очевидно, что число направляемых мод в ОВ определяется числом решений дисперсионного уравнения по заданным значениям показателей преломления 1.1.5. Число направляемых мод и длина волны отсечки Очевидно, что число направляемых мод в ОВ определяется числом решений дисперсионного уравнения по заданным значениям показателей преломления 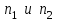 , радиуса сердцевины R и длины волны , радиуса сердцевины R и длины волны 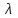 излучения, при этом изменение соотношения между указанными величинами приводит к изменению N. Общее число мод в ОВ со ступенчатым профилем показателя преломления можно определить как излучения, при этом изменение соотношения между указанными величинами приводит к изменению N. Общее число мод в ОВ со ступенчатым профилем показателя преломления можно определить как 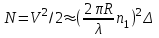 (1.54) Учитывая приведенные выше выражения для профилей показателей преломления, можно определить число мод для градиентного волокна с произвольным профилем как [2] (1.54) Учитывая приведенные выше выражения для профилей показателей преломления, можно определить число мод для градиентного волокна с произвольным профилем как [2] 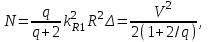 (155) а при параболическом и ступенчатом профилях (155) а при параболическом и ступенчатом профилях 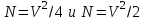 соответственно. Таким образом, при равной нормированной частоте число направляемых мод с параболическим профилем показателя преломления в 2 раза меньше, чем ступенчатого, следовательно, его характеристики передачи существенно лучше. ' 1.1.6. Диаметр модового поля Одной из основных характеристик одномодового волокна является распределение модового поля, определяемого еще как медовое пятно, диаметр которого в случае гауссова луча равен ширине кривой распределения амплитуды оптического поля на уровне 1/е или ширине кривой распределения оптической мощности (интенсивности) в точке 1/е2. Для его определения необходимо найти зависимость передаваемой мощности от смещения [7]: соответственно. Таким образом, при равной нормированной частоте число направляемых мод с параболическим профилем показателя преломления в 2 раза меньше, чем ступенчатого, следовательно, его характеристики передачи существенно лучше. ' 1.1.6. Диаметр модового поля Одной из основных характеристик одномодового волокна является распределение модового поля, определяемого еще как медовое пятно, диаметр которого в случае гауссова луча равен ширине кривой распределения амплитуды оптического поля на уровне 1/е или ширине кривой распределения оптической мощности (интенсивности) в точке 1/е2. Для его определения необходимо найти зависимость передаваемой мощности от смещения [7]: 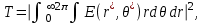 (1.56) где (1.56) где 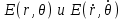 представленные в цилиндрической системе координат нормализованное распределение поперечного поля при Т = 1 и d = о и поле с переменной смещения d в направлении представленные в цилиндрической системе координат нормализованное распределение поперечного поля при Т = 1 и d = о и поле с переменной смещения d в направлении 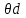 соответственно. При измерениях диаметр соответственно. При измерениях диаметр 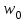 модового поля определяется с использованием функций распределения ближнего модового поля определяется с использованием функций распределения ближнего 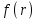 и дальнего и дальнего 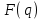 полей, определяемых как корень квадратный из значения интенсивности соответствующей световой волны, обеспечивая условие полей, определяемых как корень квадратный из значения интенсивности соответствующей световой волны, обеспечивая условие 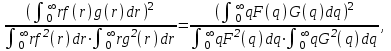 где где 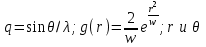 радиальное смещение и угловая координата в ближней и дальней зонах соответственно. Отсюда, определив и› или И/, значение радиуса модового поля то можно установить, используя соотношение радиальное смещение и угловая координата в ближней и дальней зонах соответственно. Отсюда, определив и› или И/, значение радиуса модового поля то можно установить, используя соотношение 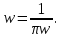 (1.57) Это определение математически эквивалентно минимизации методом наименьших квадратов уравнения: (1.57) Это определение математически эквивалентно минимизации методом наименьших квадратов уравнения: 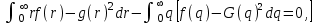 которая осуществляется в плоскости, перпендикулярной оси волокна. Данное определение диаметра модового поля дает совпадающие ре- зультаты как в ближнем, так и в дальнем поле и используется в процес- се измерений. которая осуществляется в плоскости, перпендикулярной оси волокна. Данное определение диаметра модового поля дает совпадающие ре- зультаты как в ближнем, так и в дальнем поле и используется в процес- се измерений. |
|
|
 Скачать 0.68 Mb.
Скачать 0.68 Mb.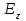 и магнитного
и магнитного 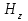 полей применительно к сердцевине двухслойного ОВ, ось которого совмещена с осью г цилиндрической системы координат, имеют вид
полей применительно к сердцевине двухслойного ОВ, ось которого совмещена с осью г цилиндрической системы координат, имеют вид 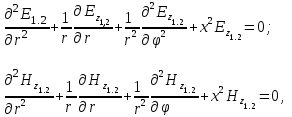 (1.41)
(1.41) 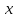 =
= 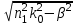 ‚ поперечный коэффициент распространения волны в сердцевине волокна: ‚
‚ поперечный коэффициент распространения волны в сердцевине волокна: ‚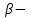 продольный коэффициент распространения;
продольный коэффициент распространения; 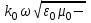 волновое число;
волновое число; 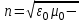 коэффициент преломления;
коэффициент преломления; 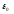 и
и 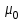 диэлектрическая и магнитная проницаемости среды, а индексы 1 и 2 соответствуют параметрам сердцевины и оболочки.
диэлектрическая и магнитная проницаемости среды, а индексы 1 и 2 соответствуют параметрам сердцевины и оболочки.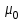 =1, а
=1, а 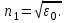 Как известно, в силу отличия физических процессов распространения волн в сердцевине и оболочке ОВ для решения данных систем уравнений используются различные функции. Так, для сердцевины решения ищутся в виде функций Бесселя и записываются как
Как известно, в силу отличия физических процессов распространения волн в сердцевине и оболочке ОВ для решения данных систем уравнений используются различные функции. Так, для сердцевины решения ищутся в виде функций Бесселя и записываются как 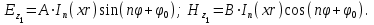 Решения уравнений для оболочки выражаются через функцию Ган- келя и имеют вид
Решения уравнений для оболочки выражаются через функцию Ган- келя и имеют вид 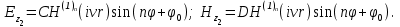 Поперечные составляющие векторов сердцевины и оболочки выражаются через комбинацию продольных составляющих
Поперечные составляющие векторов сердцевины и оболочки выражаются через комбинацию продольных составляющих 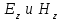 и при
и при 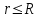 представляются в виде
представляются в виде 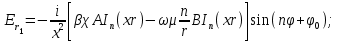
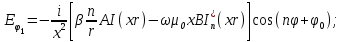
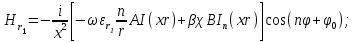
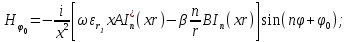 Соответственно при
Соответственно при 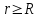 имеем
имеем 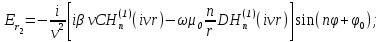
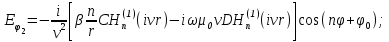
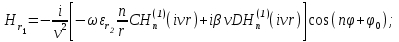
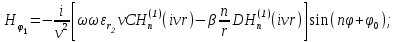 Постоянные интегрирования А, В, С, В в последних выражениях определяются из граничных условий на поверхности раздела сред при
Постоянные интегрирования А, В, С, В в последних выражениях определяются из граничных условий на поверхности раздела сред при 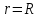 которые задаются как
которые задаются как 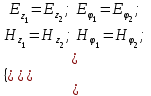 В результате имеет место следующая однородная система уравнений:
В результате имеет место следующая однородная система уравнений: 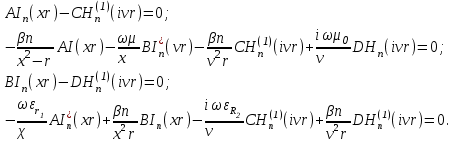 Приравнивая к нулю определитель полученной системы уравнений, решение ищется относительно д в виде так называемого основного дисперсионного уравнения [2]:
Приравнивая к нулю определитель полученной системы уравнений, решение ищется относительно д в виде так называемого основного дисперсионного уравнения [2]: 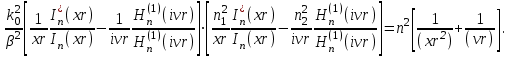 (1.42) Данное уравнение позволяет найти решение относительно
(1.42) Данное уравнение позволяет найти решение относительно 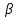 и рассчитать структуру поля в сердцевине и оболочке ОВ, зная значения поперечных коэффициентов распространения
и рассчитать структуру поля в сердцевине и оболочке ОВ, зная значения поперечных коэффициентов распространения 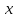 и
и 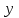 . В общем случае уравнения такого вида имеют ряд решений, каждому из которых соответствует определенный тип волны, называемый модой, которая определяется сложностью структуры поля, в частности числом максимумов и минимумов в поперечном сечении, и обозначается двумя числовыми индексами nи m. Индекс п означает число изменений поля по периметру ОВ, а индекс m - число изменений поля по диаметру. В оптическом волокне могут распространяться два типа волн: симметричные продольные
. В общем случае уравнения такого вида имеют ряд решений, каждому из которых соответствует определенный тип волны, называемый модой, которая определяется сложностью структуры поля, в частности числом максимумов и минимумов в поперечном сечении, и обозначается двумя числовыми индексами nи m. Индекс п означает число изменений поля по периметру ОВ, а индекс m - число изменений поля по диаметру. В оптическом волокне могут распространяться два типа волн: симметричные продольные 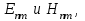 , у которых по одной продольной составляющей, и несимметричные волны, имеющие одновременно по две продольные составляющие, одна из которых
, у которых по одной продольной составляющей, и несимметричные волны, имеющие одновременно по две продольные составляющие, одна из которых 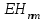 с преобладанием электрической составляющей Е: и другая НЕМ" с преобладанием магнитной составляющей Н. Следует отметить, что, связывая электромагнитную теорию с лучевой теорией, симметричные волны будут соответствовать меридианным лучам, а несимметричные — косым лучам. В случае симметричных мод, у которых поле не зависит от азиму- тального угла ф, правая часть дисперсионного уравнения равна нулю, и оно распадается на два уравнения:
с преобладанием электрической составляющей Е: и другая НЕМ" с преобладанием магнитной составляющей Н. Следует отметить, что, связывая электромагнитную теорию с лучевой теорией, симметричные волны будут соответствовать меридианным лучам, а несимметричные — косым лучам. В случае симметричных мод, у которых поле не зависит от азиму- тального угла ф, правая часть дисперсионного уравнения равна нулю, и оно распадается на два уравнения: 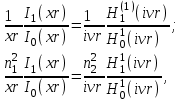 (1.43) первое из которых определяет характеристики составляющих направленных магнитных Н-мод, в которых
(1.43) первое из которых определяет характеристики составляющих направленных магнитных Н-мод, в которых 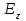 =0‚
=0‚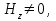 а второе -— электрических Е-мод с
а второе -— электрических Е-мод с 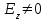 и
и 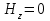 . Очевидно, что изменение значений
. Очевидно, что изменение значений 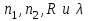 приводит к изменению числа решении данных дисперсионных уравнений и, следовательно, числа распространяющихся в волокне симметричных мод. 1.1.4. Нормированная и критическая частота Условием существования направляемой моды является экспоненциальное убывание ее поля в оболочке вдоль координаты r, причем степень уменьшения напряженности с ростом r определяется значением v, уменьшение которой приводит к перераспределению поля в оболочку ОВ – появлению вытекающих волн. При v=0 происходит качественное изменение волнового процесса, заключающегося в невозможности существования направляемой моды. Этот режим называется критическим, в связи с чем очень важно определение условий его возникновения, что можно осуществить подстановкой в последнее уравнение значения v=0, в результате правые части уравнений обращаются в бесконечность и для Е и Н мод будет справедливо условие
приводит к изменению числа решении данных дисперсионных уравнений и, следовательно, числа распространяющихся в волокне симметричных мод. 1.1.4. Нормированная и критическая частота Условием существования направляемой моды является экспоненциальное убывание ее поля в оболочке вдоль координаты r, причем степень уменьшения напряженности с ростом r определяется значением v, уменьшение которой приводит к перераспределению поля в оболочку ОВ – появлению вытекающих волн. При v=0 происходит качественное изменение волнового процесса, заключающегося в невозможности существования направляемой моды. Этот режим называется критическим, в связи с чем очень важно определение условий его возникновения, что можно осуществить подстановкой в последнее уравнение значения v=0, в результате правые части уравнений обращаются в бесконечность и для Е и Н мод будет справедливо условие 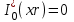 (1.44) которое определяет границы их возникновения или исчезновения. Последнее уравнение имеет бесчисленное множество решений, поэтому, обозначив положительный корень через
(1.44) которое определяет границы их возникновения или исчезновения. Последнее уравнение имеет бесчисленное множество решений, поэтому, обозначив положительный корень через 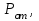 а также используя выражения для у и у, мы получаем
а также используя выражения для у и у, мы получаем 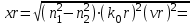
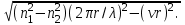 Введем величину, которая носит название нормированной частоты:
Введем величину, которая носит название нормированной частоты: 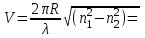
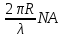 (1.45) Это один из важнейших обобщающих параметров, используемых для оценки свойств ОВ, который связывает его структурные параметры и длину световой волны аспространяемой в волокне. Тогда
(1.45) Это один из важнейших обобщающих параметров, используемых для оценки свойств ОВ, который связывает его структурные параметры и длину световой волны аспространяемой в волокне. Тогда 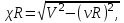 и при v=0 для каждого из корней имеет место критическое значение нормированной частоты:
и при v=0 для каждого из корней имеет место критическое значение нормированной частоты: 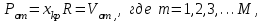 (1.46) A
(1.46) A 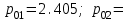 5.520;
5.520;  Если для некоторой симметричной моды нормированная частота больше ее критического значения
Если для некоторой симметричной моды нормированная частота больше ее критического значения 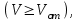 то она распространяется в ОВ, в противном случае ее нет. Так, при 2.4О5<У<5.52О в ОВ распространяются моды
то она распространяется в ОВ, в противном случае ее нет. Так, при 2.4О5<У<5.52О в ОВ распространяются моды 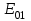 , и
, и 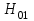 , а при 5.520<У<8.6`54 к ним добавляются моды Е”, Но, и т. д., в то время как неравенство У<2.4О5 указывает на отсутствие симметричных мод. Последняя формула позволяет определить значения критических длин волн
, а при 5.520<У<8.6`54 к ним добавляются моды Е”, Но, и т. д., в то время как неравенство У<2.4О5 указывает на отсутствие симметричных мод. Последняя формула позволяет определить значения критических длин волн 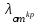 для симметричных волн в виде [2]
для симметричных волн в виде [2] 
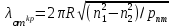

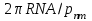 (1.47) или, переходя к частоте,
(1.47) или, переходя к частоте, 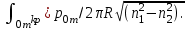 (1.48) Очевидно, что для распространяющейся моды должно выполняться условие ‚
(1.48) Очевидно, что для распространяющейся моды должно выполняться условие ‚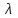 <
<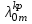 , т. е.
, т. е. 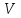 >
>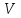 ‚ в противном случае этой моды нет. В отличие от симметричных мод несимметричные имеют все шесть составляющих векторов электромагнитного поля и их невозможно разделить на электрические и магнитные. Критическая нормирования частоте в этом случае определяется выражением
‚ в противном случае этой моды нет. В отличие от симметричных мод несимметричные имеют все шесть составляющих векторов электромагнитного поля и их невозможно разделить на электрические и магнитные. Критическая нормирования частоте в этом случае определяется выражением 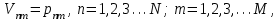 (1.49) В результате чего при заданных параметрах ОВ критическая длина волны равна
(1.49) В результате чего при заданных параметрах ОВ критическая длина волны равна 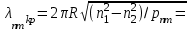
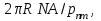 (1.50) где
(1.50) где 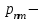 положительный корень соответствующего трансцендентного уравнения:
положительный корень соответствующего трансцендентного уравнения: 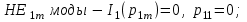
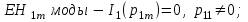 (1.51)
(1.51) 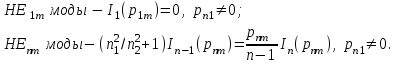 Указанные уравнения также получены из основного дисперсионного уравнения при v=0. Среди направляемых мод особое положение занимает мода НЕ11, у которой критическое значение нормированной частоты V11=0. Это основная (фундаментальная) мода ступенчатого ОВ, так как она распространяется при любой частоте и структурных параметрах волокна. С точки зрения геометрической оптики, она образуется лучом, вводимым вдоль оси волокна, так как только характеристики такого луча не зависят от условий отражения на границе “сердцевина — оболочка". Выбирая параметры ОВ, можно получить режим распространения только этой моды, что реализуется при условии
Указанные уравнения также получены из основного дисперсионного уравнения при v=0. Среди направляемых мод особое положение занимает мода НЕ11, у которой критическое значение нормированной частоты V11=0. Это основная (фундаментальная) мода ступенчатого ОВ, так как она распространяется при любой частоте и структурных параметрах волокна. С точки зрения геометрической оптики, она образуется лучом, вводимым вдоль оси волокна, так как только характеристики такого луча не зависят от условий отражения на границе “сердцевина — оболочка". Выбирая параметры ОВ, можно получить режим распространения только этой моды, что реализуется при условии 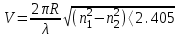 (152) Минимальная длина волны, при которой в волокне распространяется фундаментальная мода, называется волоконной длиной волны отсечки, значение которой легко определяется из последнего выражения как
(152) Минимальная длина волны, при которой в волокне распространяется фундаментальная мода, называется волоконной длиной волны отсечки, значение которой легко определяется из последнего выражения как 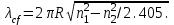 (1-53) Однако на практике больший интерес представляет так называемая кабельная длина волны отсечки
(1-53) Однако на практике больший интерес представляет так называемая кабельная длина волны отсечки 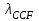 , которая смещена относительно
, которая смещена относительно 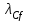 , в область более коротких волн из-за влияния механических напряжений, возникающих при укладке оптического волокна в кабель. Ввиду сложности теоретического учета влияния данных воздействий для определения
, в область более коротких волн из-за влияния механических напряжений, возникающих при укладке оптического волокна в кабель. Ввиду сложности теоретического учета влияния данных воздействий для определения 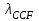 используется экспериментальные методы. При увеличении нормированной частоты в ОВ появляются другие моды, которые принято называть высшими. Каждая из этих мод обладает характерной для нее структурой электромагнитного поля в сердцевине и оболочке, а также запаздыванием по фазе
используется экспериментальные методы. При увеличении нормированной частоты в ОВ появляются другие моды, которые принято называть высшими. Каждая из этих мод обладает характерной для нее структурой электромагнитного поля в сердцевине и оболочке, а также запаздыванием по фазе 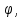 которое для симметричных и несимметричных мод определяется в результате численного решения соответствующих дисперсионных уравнений. На практике вместо дисперсионных характеристик
которое для симметричных и несимметричных мод определяется в результате численного решения соответствующих дисперсионных уравнений. На практике вместо дисперсионных характеристик 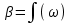 удобнее использовать нормированные дисперсионные параметры
удобнее использовать нормированные дисперсионные параметры 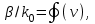 которые описывают свойства всех ступенчатых ОВ. Лучевая трактовка до иллюстрируется рис. 1.6, на котором показан процесс распространения меридианных лучей по двухслойному волокну. Здесь показаны предельные случаи распространения малых длин волн и волн, соизмеримых с диаметром сердцевины волокна. Рис. 1.6. Распространение излучения по ступенчатому волокну при различных частотах оптического излучения В первом случае, когда
которые описывают свойства всех ступенчатых ОВ. Лучевая трактовка до иллюстрируется рис. 1.6, на котором показан процесс распространения меридианных лучей по двухслойному волокну. Здесь показаны предельные случаи распространения малых длин волн и волн, соизмеримых с диаметром сердцевины волокна. Рис. 1.6. Распространение излучения по ступенчатому волокну при различных частотах оптического излучения В первом случае, когда 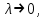 угол
угол 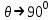 и, следовательно, волна стремится к более предпочтительному прямолинейному движению вдоль оси волокна, а во втором случае ‚
и, следовательно, волна стремится к более предпочтительному прямолинейному движению вдоль оси волокна, а во втором случае ‚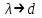 и
и 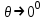 - волна претерпевает большое число отражений, в связи с чем значительно увеличивается длина пути оптического луча. При определенной длине волны наступает такой режим, при котором
- волна претерпевает большое число отражений, в связи с чем значительно увеличивается длина пути оптического луча. При определенной длине волны наступает такой режим, при котором 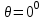 , и волна, падая на границу “сердцевина — оболочка”, отражается от нее под прямым углом. В этом случае в ОВ устанавливается режим стоячей волны, и энергия вдоль волокна не распространяется, что соответствует случаю критической длины волны. Поэтому по ОВ возможна передача электромагнитного излучения только с длиной волны, меньшей диаметра волокна, т. е.
, и волна, падая на границу “сердцевина — оболочка”, отражается от нее под прямым углом. В этом случае в ОВ устанавливается режим стоячей волны, и энергия вдоль волокна не распространяется, что соответствует случаю критической длины волны. Поэтому по ОВ возможна передача электромагнитного излучения только с длиной волны, меньшей диаметра волокна, т. е. 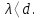 1.1.5. Число направляемых мод и длина волны отсечки Очевидно, что число направляемых мод в ОВ определяется числом решений дисперсионного уравнения по заданным значениям показателей преломления
1.1.5. Число направляемых мод и длина волны отсечки Очевидно, что число направляемых мод в ОВ определяется числом решений дисперсионного уравнения по заданным значениям показателей преломления 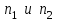 , радиуса сердцевины R и длины волны
, радиуса сердцевины R и длины волны 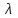 излучения, при этом изменение соотношения между указанными величинами приводит к изменению N. Общее число мод в ОВ со ступенчатым профилем показателя преломления можно определить как
излучения, при этом изменение соотношения между указанными величинами приводит к изменению N. Общее число мод в ОВ со ступенчатым профилем показателя преломления можно определить как 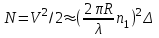 (1.54) Учитывая приведенные выше выражения для профилей показателей преломления, можно определить число мод для градиентного волокна с произвольным профилем как [2]
(1.54) Учитывая приведенные выше выражения для профилей показателей преломления, можно определить число мод для градиентного волокна с произвольным профилем как [2] 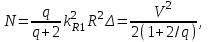 (155) а при параболическом и ступенчатом профилях
(155) а при параболическом и ступенчатом профилях 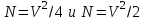 соответственно. Таким образом, при равной нормированной частоте число направляемых мод с параболическим профилем показателя преломления в 2 раза меньше, чем ступенчатого, следовательно, его характеристики передачи существенно лучше. ' 1.1.6. Диаметр модового поля Одной из основных характеристик одномодового волокна является распределение модового поля, определяемого еще как медовое пятно, диаметр которого в случае гауссова луча равен ширине кривой распределения амплитуды оптического поля на уровне 1/е или ширине кривой распределения оптической мощности (интенсивности) в точке 1/е2. Для его определения необходимо найти зависимость передаваемой мощности от смещения [7]:
соответственно. Таким образом, при равной нормированной частоте число направляемых мод с параболическим профилем показателя преломления в 2 раза меньше, чем ступенчатого, следовательно, его характеристики передачи существенно лучше. ' 1.1.6. Диаметр модового поля Одной из основных характеристик одномодового волокна является распределение модового поля, определяемого еще как медовое пятно, диаметр которого в случае гауссова луча равен ширине кривой распределения амплитуды оптического поля на уровне 1/е или ширине кривой распределения оптической мощности (интенсивности) в точке 1/е2. Для его определения необходимо найти зависимость передаваемой мощности от смещения [7]: 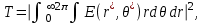 (1.56) где
(1.56) где 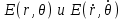 представленные в цилиндрической системе координат нормализованное распределение поперечного поля при Т = 1 и d = о и поле с переменной смещения d в направлении
представленные в цилиндрической системе координат нормализованное распределение поперечного поля при Т = 1 и d = о и поле с переменной смещения d в направлении 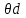 соответственно. При измерениях диаметр
соответственно. При измерениях диаметр 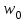 модового поля определяется с использованием функций распределения ближнего
модового поля определяется с использованием функций распределения ближнего 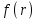 и дальнего
и дальнего 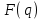 полей, определяемых как корень квадратный из значения интенсивности соответствующей световой волны, обеспечивая условие
полей, определяемых как корень квадратный из значения интенсивности соответствующей световой волны, обеспечивая условие 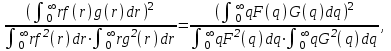 где
где 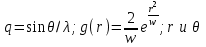 радиальное смещение и угловая координата в ближней и дальней зонах соответственно. Отсюда, определив и› или И/, значение радиуса модового поля то можно установить, используя соотношение
радиальное смещение и угловая координата в ближней и дальней зонах соответственно. Отсюда, определив и› или И/, значение радиуса модового поля то можно установить, используя соотношение 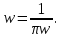 (1.57) Это определение математически эквивалентно минимизации методом наименьших квадратов уравнения:
(1.57) Это определение математически эквивалентно минимизации методом наименьших квадратов уравнения: 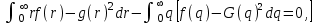 которая осуществляется в плоскости, перпендикулярной оси волокна. Данное определение диаметра модового поля дает совпадающие ре- зультаты как в ближнем, так и в дальнем поле и используется в процес- се измерений.
которая осуществляется в плоскости, перпендикулярной оси волокна. Данное определение диаметра модового поля дает совпадающие ре- зультаты как в ближнем, так и в дальнем поле и используется в процес- се измерений. 