|
|
ВОЛС. Оптическое волокно Сандугаш. Волоконнооптические
1 .1 .З. Исходные положения и допущения волновой теории Так как свет представляет собой электромагнитную волну, а ее распространение в любой среде описывается уравнениями Максвелла, распро- странение света может рассматриваться путем определения развития связанных с ним векторов электрического 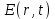 и магнитного и магнитного 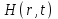 полей в пространстве и времени. Здесь r обозначает положение вектора, а t — время. Иногда более удобно иметь дело с преобразованием Фурье этих векторов, которое для вектора Е определяется следующим образом [4]: полей в пространстве и времени. Здесь r обозначает положение вектора, а t — время. Иногда более удобно иметь дело с преобразованием Фурье этих векторов, которое для вектора Е определяется следующим образом [4]: 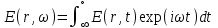 (1.20) Преобразование Фурье для вектора Н и других векторов определяется аналогичным образом. Очевидно, что даже когда Е(r,t) реально, E(r,w) может быть комплексным, несмотря на это, во многих случаях оказывается очень удобным представлять Е(г,1) также в комплексном виде, принимая во внимание только реальную часть полученных решений. Как известно, электроны в атоме заряжены отрицательно, а ядро несет положительный заряд, поэтому, когда электрическое поле прилагается к материалу, подобному кварцу, силы, испытываемые ядрами и электронами, имеют противоположные направления, что приводит к поляризации атомов. индуцированная электрическая поляризация материала, или просто поляризация, может быть описана при помощи вектора ЕР’, который зависит как от особенностей материала, так и прилагаемого поля. индуцированная поляризация может быть рассмотрена как отклик среды на прилагаемое электрическое поле. Рассмотрим связь Р и Е более подробно, определив вначале вектор В, называемый электрической индукцией, который связан с электрическим полем Е и электрической поляризацией Р, следующим образом: (1.20) Преобразование Фурье для вектора Н и других векторов определяется аналогичным образом. Очевидно, что даже когда Е(r,t) реально, E(r,w) может быть комплексным, несмотря на это, во многих случаях оказывается очень удобным представлять Е(г,1) также в комплексном виде, принимая во внимание только реальную часть полученных решений. Как известно, электроны в атоме заряжены отрицательно, а ядро несет положительный заряд, поэтому, когда электрическое поле прилагается к материалу, подобному кварцу, силы, испытываемые ядрами и электронами, имеют противоположные направления, что приводит к поляризации атомов. индуцированная электрическая поляризация материала, или просто поляризация, может быть описана при помощи вектора ЕР’, который зависит как от особенностей материала, так и прилагаемого поля. индуцированная поляризация может быть рассмотрена как отклик среды на прилагаемое электрическое поле. Рассмотрим связь Р и Е более подробно, определив вначале вектор В, называемый электрической индукцией, который связан с электрическим полем Е и электрической поляризацией Р, следующим образом: 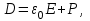 (1.21) где (1.21) где 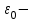 -постоянная, называемая относительной диэлектрической проницаемостью среды, в нашем случае вакуума. Электрическая индукция в вакууме равна . Аналогично определяется связь магнитной поляризации -постоянная, называемая относительной диэлектрической проницаемостью среды, в нашем случае вакуума. Электрическая индукция в вакууме равна . Аналогично определяется связь магнитной поляризации 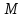 и маг- нитной индукции В и маг- нитной индукции В 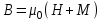 (1.22) Однако, так как кварц является немагнитным материалом, (1.22) Однако, так как кварц является немагнитным материалом, 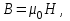 где где 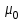 ‚но есть постоянная, называемая магнитной проницаемостью вакума. Таким образом уравнения Максвелла учитывают влияние характеристик материала на распространение электромагнитных волн, так как они используют не только Е и Н, но и электрическую D , и магнитную В индукцию. Связь P и Е в оптическом волокне определяется свойствами среды (кварца) и является причиной двух важных явлений, относящихся к распространению в нем света, — дисперсии и нелинейным эффектам, которые налагают ограничения на функционирование современных коммуникационных систем. Рассмотрим пять фундаментальных характеристик среды и их влияние на связь между индуцированной поляризацией Р в среде и воздействующим электрическим полем Е. Локальность отклика. В среде, отклик которой на прилагаемое электрическое поле является локальным и когда ‚но есть постоянная, называемая магнитной проницаемостью вакума. Таким образом уравнения Максвелла учитывают влияние характеристик материала на распространение электромагнитных волн, так как они используют не только Е и Н, но и электрическую D , и магнитную В индукцию. Связь P и Е в оптическом волокне определяется свойствами среды (кварца) и является причиной двух важных явлений, относящихся к распространению в нем света, — дисперсии и нелинейным эффектам, которые налагают ограничения на функционирование современных коммуникационных систем. Рассмотрим пять фундаментальных характеристик среды и их влияние на связь между индуцированной поляризацией Р в среде и воздействующим электрическим полем Е. Локальность отклика. В среде, отклик которой на прилагаемое электрическое поле является локальным и когда 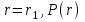 , зависит только от , зависит только от 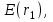 значения Е (r) для значения Е (r) для 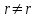 , не оказывают влияния на , не оказывают влияния на 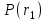 . Это свойство соблюдается с достаточно высокой степенью приближения для кварцевого волокна в диапазоне длин волн от 0.5 мкм до 2 мкм, который и используется в оптических коммуникационных системах. Изотропия. Изотропная среда характеризуется тем, что ее электро-магнитные свойства, такие, как показатель преломления, одинаковы во всех направлениях. В изотропной среде . Это свойство соблюдается с достаточно высокой степенью приближения для кварцевого волокна в диапазоне длин волн от 0.5 мкм до 2 мкм, который и используется в оптических коммуникационных системах. Изотропия. Изотропная среда характеризуется тем, что ее электро-магнитные свойства, такие, как показатель преломления, одинаковы во всех направлениях. В изотропной среде 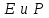 являются векторами одинаковой ориентации, и так как кварц представляет собой изотропную среду, идеально цилиндрическое оптическое волокно также является изотропным. Среда, показатели преломления которой вдоль двух отличных направлений соответствующей системы координат, например вдоль осей х и у, различны, называется двулучепреломляющей, поэтому оптическое волокно, не обладающее цилиндрической симметрией, также называется двулучепреломляющим. Двулучепреломление ряда материалов, таких, как ниобат лития, используется в ряде волоконно-оптических компонентов, таких, как модуляторы, изоляторы и настраиваемые фильтры. Линейность. В линейной изотропной среде являются векторами одинаковой ориентации, и так как кварц представляет собой изотропную среду, идеально цилиндрическое оптическое волокно также является изотропным. Среда, показатели преломления которой вдоль двух отличных направлений соответствующей системы координат, например вдоль осей х и у, различны, называется двулучепреломляющей, поэтому оптическое волокно, не обладающее цилиндрической симметрией, также называется двулучепреломляющим. Двулучепреломление ряда материалов, таких, как ниобат лития, используется в ряде волоконно-оптических компонентов, таких, как модуляторы, изоляторы и настраиваемые фильтры. Линейность. В линейной изотропной среде 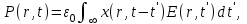 (1.23) где (1.23) где 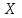 называется чувствительностью, или, более точно, чувствительностью линейной среды. Таким образом, индуцированная поляризация получается путем свертки прилагаемого электрического поля. Если называется чувствительностью, или, более точно, чувствительностью линейной среды. Таким образом, индуцированная поляризация получается путем свертки прилагаемого электрического поля. Если 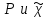 обозначают соответственно преобразования Фурье обозначают соответственно преобразования Фурье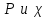 , (1.2З) примет вид , (1.2З) примет вид 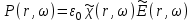 (1.24) В этом случае индуцированная поляризация может рассматриваться как выход линейной системы с входным сигналом (1.24) В этом случае индуцированная поляризация может рассматриваться как выход линейной системы с входным сигналом 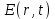 или или 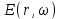 импульсным откликом импульсным откликом 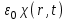 и функцией преобразования и функцией преобразования 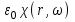 . Таким образом, отклик среды на прилагаемое электрическое поле не является мгновенным, так как . Таким образом, отклик среды на прилагаемое электрическое поле не является мгновенным, так как 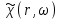 зависит от зависит от 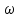 Это является причиной важного эффекта, свойственного распространению света в оптическом волокне, — дисперсии, в данном случае хроматической дисперсии, налагающей основное ограничение на функционирование оптических систем передачи. Таким образом, происхождение хроматической дисперсии кроется в задержке отклика индуцированной поляризации в кварцевой среде на действие прилагаемого электрического поля. Подобное линейное соотношение связи Это является причиной важного эффекта, свойственного распространению света в оптическом волокне, — дисперсии, в данном случае хроматической дисперсии, налагающей основное ограничение на функционирование оптических систем передачи. Таким образом, происхождение хроматической дисперсии кроется в задержке отклика индуцированной поляризации в кварцевой среде на действие прилагаемого электрического поля. Подобное линейное соотношение связи 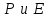 реально не соблюдается для кварца, однако обладает достаточно высокой степенью приближения для сигналов средней мощности и умеренной битовой скорости. Влияние поляризационной модовой дисперсии и нелинейных явлений на распространение света будет дано позже. Однородность. Однородная среда характеризуется тем, что электромагнитные характеристики реально не соблюдается для кварца, однако обладает достаточно высокой степенью приближения для сигналов средней мощности и умеренной битовой скорости. Влияние поляризационной модовой дисперсии и нелинейных явлений на распространение света будет дано позже. Однородность. Однородная среда характеризуется тем, что электромагнитные характеристики 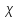 и, соответственно‚ и, соответственно‚ 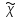 не зависят от положения вектора не зависят от положения вектора 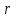 , поэтому , поэтому 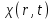 в этом случае можно заменить на в этом случае можно заменить на 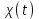 Однако, несмотря на то, что кварц является однородной средой, оптическое волокво неоднородно из-за того, что показатели преломления сердцевины и оболочки различны. Поэтому области сердцевины и оболочки в волокне со ступенчато изменяющимся показателем преломления могут рассматриваться раздельно как однородные среды, в то время как в градиентном волокне это допущение неприемлемо ввиду его неоднородной сердцевины. Отсутствие потерь. Хотя нельзя говорить, что кварцевое волокно функционирует без потерь, при рассмотрении распространения мод потерями можно пренебречь, приравняв их к нулю, так как параметры этих мод не будут существенно изменяться при таком допущении. Таким образом, принятые допущения, заключающиеся в том, что области сердцевины и оболочки кварцевого волокна являются локально чувствительными, изотропными, линейными, однородными и обладают нулевым показателем потерь, соответствуют идеализированному оптическому волокну. В то же время, учитывая, что чувствительность 2 является более фундаментальной характеристикой материала, чем показатель преломления п ‚ выраженный отношением скорости света в вакууме к скорости света в материале волокна, определим последний в терминах чувствительности Однако, несмотря на то, что кварц является однородной средой, оптическое волокво неоднородно из-за того, что показатели преломления сердцевины и оболочки различны. Поэтому области сердцевины и оболочки в волокне со ступенчато изменяющимся показателем преломления могут рассматриваться раздельно как однородные среды, в то время как в градиентном волокне это допущение неприемлемо ввиду его неоднородной сердцевины. Отсутствие потерь. Хотя нельзя говорить, что кварцевое волокно функционирует без потерь, при рассмотрении распространения мод потерями можно пренебречь, приравняв их к нулю, так как параметры этих мод не будут существенно изменяться при таком допущении. Таким образом, принятые допущения, заключающиеся в том, что области сердцевины и оболочки кварцевого волокна являются локально чувствительными, изотропными, линейными, однородными и обладают нулевым показателем потерь, соответствуют идеализированному оптическому волокну. В то же время, учитывая, что чувствительность 2 является более фундаментальной характеристикой материала, чем показатель преломления п ‚ выраженный отношением скорости света в вакууме к скорости света в материале волокна, определим последний в терминах чувствительности 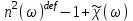 (1.25) и будем рассматривать его как функцию угловой частоты (1.25) и будем рассматривать его как функцию угловой частоты 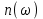 аналогично (1.25). Для волокна со значением аналогично (1.25). Для волокна со значением 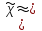 1.25 и показателем преломления 1.25 и показателем преломления 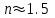 1.1.3.1. Волновые уравнения В общем случае распространение электромагнитных волн описывается системой основных уравнений Максвелла в векторной форме [5] 1.1.3.1. Волновые уравнения В общем случае распространение электромагнитных волн описывается системой основных уравнений Максвелла в векторной форме [5] 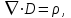 (1.26) (1.26) 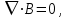 (1.27) (1.27) 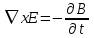 (1.28) (1.28) 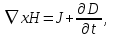 (1.29) где (1.29) где 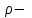 плотность электрического заряда; плотность электрического заряда; 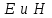 - напряженность электрического и магнитного полей; - напряженность электрического и магнитного полей; 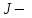 плотность тока; плотность тока; 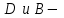 электрическая и магнитная индукции. Таким образом, уравнения Максвелла учитывают влияние характеристик материала на распространение электромагнитных волн, так как в них входит не только электрическая и магнитная индукции. Таким образом, уравнения Максвелла учитывают влияние характеристик материала на распространение электромагнитных волн, так как в них входит не только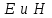 , но и D и B. Предположив, что в среде нет свободных зарядов, т. е. , но и D и B. Предположив, что в среде нет свободных зарядов, т. е.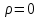 , следовательно, , следовательно, 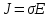 ‚ а так как проводимость кварца очень низка, т. е. ‚ а так как проводимость кварца очень низка, т. е. 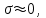 можно заключить, что можно заключить, что 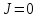 . Тогда, используя (1.21) и (1.22)‚ а также исключив индукцию из уравнений (1.28) и (1.29)‚ представим уравнения Максвелла только в терминах полей . Тогда, используя (1.21) и (1.22)‚ а также исключив индукцию из уравнений (1.28) и (1.29)‚ представим уравнения Максвелла только в терминах полей 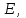 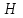 и поляризации P [5]: и поляризации P [5]: 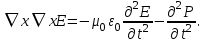 (1.30) Чтобы решить это уравнение относительно Е, необходимо соотнести (1.30) Чтобы решить это уравнение относительно Е, необходимо соотнести 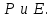 Без учета нелинейных эффектов можно допустить, что связь Без учета нелинейных эффектов можно допустить, что связь 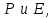 имеет линейный характер, определяемый выражением (1.24), и. более того, вследствие предположения об однородности можно вместо имеет линейный характер, определяемый выражением (1.24), и. более того, вследствие предположения об однородности можно вместо 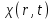 записать записать 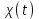 ослабив это предположение при рассмотрении нелинейных явлений. Решить (1.30) относительно ослабив это предположение при рассмотрении нелинейных явлений. Решить (1.30) относительно 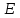 наиболее удобно посредством преобразования Фурье [5], которое для наиболее удобно посредством преобразования Фурье [5], которое для 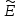 от от 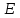 определяется согласно (1.20)‚ а для определяется согласно (1.20)‚ а для 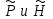 находится аналогичным образом. В результате находится аналогичным образом. В результате 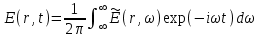 (1.31) Путем дифференцирования этого уравнения относительно (1.31) Путем дифференцирования этого уравнения относительно 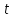 имеем преобразование Фурье для имеем преобразование Фурье для 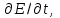 равное - равное -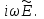 Принимая во внимание преобразование Фурье (1.30), имеем Принимая во внимание преобразование Фурье (1.30), имеем 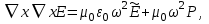 затем, используя (1.24) для выражения затем, используя (1.24) для выражения 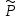  в терминах в терминах 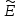 , сведем его до уравнения вида , сведем его до уравнения вида 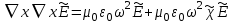 Введем с =1/ Введем с =1/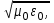 где с — скорость света в вакууме, пренебрегая потерями и принимая где с — скорость света в вакууме, пренебрегая потерями и принимая 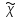 за реальную величину, можно записать за реальную величину, можно записать 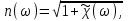 где где 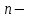 показатель преломления, тогда показатель преломления, тогда 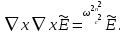 Используя идентичность Используя идентичность 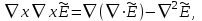 уравнение (1.32) можно преобразовать к виду уравнение (1.32) можно преобразовать к виду 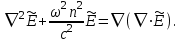 (1.33) Допуская однородность среды ( (1.33) Допуская однородность среды (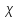 не зависит от не зависит от 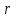 ), а также используя (1.26) и (1.25), имеем ), а также используя (1.26) и (1.25), имеем 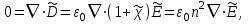 (1.34) что позволяет упростить (1.3З) и получить волновое уравнение для Е в виде (1.34) что позволяет упростить (1.3З) и получить волновое уравнение для Е в виде 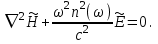 (1.35) Выполняя аналогичные операции, можно вывести волновое уравнение и для (1.35) Выполняя аналогичные операции, можно вывести волновое уравнение и для 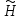 : : 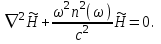 (1.36) Здесь (1.36) Здесь 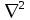 обозначает оператор Лапласа, который определяется в прямоугольной системе координат выражением обозначает оператор Лапласа, который определяется в прямоугольной системе координат выражением 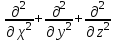 . Таким образом, волновые уравнения представляют собой линейные дифференциальные уравнения в частных производных второго порядка для преобразования Фурье векторов электрического и магнитного поля. На самом деле каждое уравнение волны отражает три уравнения — по одному на каждый компонент вектора соответствующего поля. 1.1.З.2. Поляризация световых волн Как было показано выше, мода распространяемой в волокне световой волны определяется как решение волнового уравнения, которое удовлетворяет граничным условиям на разделе сердцевина — оболочка. При этом имеют место два линейно независимых решения волновых уравнений для всех . Таким образом, волновые уравнения представляют собой линейные дифференциальные уравнения в частных производных второго порядка для преобразования Фурье векторов электрического и магнитного поля. На самом деле каждое уравнение волны отражает три уравнения — по одному на каждый компонент вектора соответствующего поля. 1.1.З.2. Поляризация световых волн Как было показано выше, мода распространяемой в волокне световой волны определяется как решение волнового уравнения, которое удовлетворяет граничным условиям на разделе сердцевина — оболочка. При этом имеют место два линейно независимых решения волновых уравнений для всех 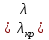 вне зависимости от того, насколько велики их значения. Эти решения соответствуют фундаментальной моде и имеют идентичную постоянную распространения. Другие решения существуют только когда вне зависимости от того, насколько велики их значения. Эти решения соответствуют фундаментальной моде и имеют идентичную постоянную распространения. Другие решения существуют только когда 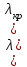 . Рассмотрим поведение фундаментальной моды, представив электрическое поле . Рассмотрим поведение фундаментальной моды, представив электрическое поле 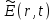 световой волны в виде световой волны в виде 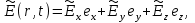 (1‚37) где (1‚37) где 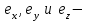 соответственно единичные векторы вдоль осей соответственно единичные векторы вдоль осей 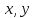 и и 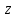 , причем , причем 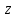 — направление распространения световой волны (ось волокна), а каждое значение — направление распространения световой волны (ось волокна), а каждое значение 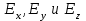 может зависеть в основном от может зависеть в основном от 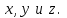 Как показано в [5], данное уравнение имеет два линейно независимых решения (1.35), которые соответствуют фундаментальной моде, при этом одно изрешений соответствует Как показано в [5], данное уравнение имеет два линейно независимых решения (1.35), которые соответствуют фундаментальной моде, при этом одно изрешений соответствует 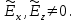 когда когда 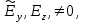 а другое а другое 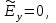 когда когда 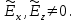 Так как z является также направлением распространения, Так как z является также направлением распространения, 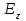 называется продольной компонентой. Другой ненулевой компонент, то есть называется продольной компонентой. Другой ненулевой компонент, то есть 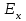 , или , или 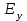 , называется поперечной компонентой. Для фундаментальной моды продольный и поперечный компоненты могут быть представлены в виде , называется поперечной компонентой. Для фундаментальной моды продольный и поперечный компоненты могут быть представлены в виде 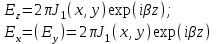 (1.38), (1.39) где . (1.38), (1.39) где . 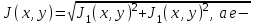 вследствие цилиндрической симметрии волокна являются функцией вследствие цилиндрической симметрии волокна являются функцией 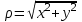 и представляют собой функцию Бесселя. Для определения в частотной области каждого из решений, соответ- ствующего фундаментальной моде, заменим и представляют собой функцию Бесселя. Для определения в частотной области каждого из решений, соответ- ствующего фундаментальной моде, заменим 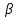 на на 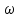 тогда тогда 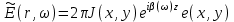 (1.40) где (1.40) где 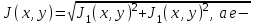 единичный вектор вдоль направления единичный вектор вдоль направления 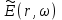 . В общем случае, конечно, . В общем случае, конечно, 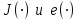 также являются функциями также являются функциями 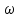 , но этой зависимостью можно пренебречь для импульсов, ширина спектра которых значительно меньше их центральной частоты, что соответствует импульсам, используемым в оптических коммуникационных системах. Прежде чем продолжить рассмотрение распределения электрического поля фундаментальной моды, необходимо понять концепцию поляризации электрического поля, представляющего собой вектор электрического поля‚ размер и направление которого могут изменяться со временем. Изменяющееся со временем электрическое поле считается линейно поляризованным, если его направление является постоянным, т. е. не зависит от времени. Так, если электрическое поле, ассоциируемое с электромагнитной волной, не имеет компоненты вдоль направления распространения волны, электрическое поле считается поперечным, а в противном случае — продольным. Для фундаментальной моды одномодового волокна величина продольной компоненты Е, значительно меньше величины поперечной компоненты Е, или Е у. Поэтому электрическое поле фундаментальной моды с большой долей вероятности является поперечным полем. Учитывая это предположение, два линейно независимых решения волнового уравнения представляют линейно поляризованные вдоль осей , но этой зависимостью можно пренебречь для импульсов, ширина спектра которых значительно меньше их центральной частоты, что соответствует импульсам, используемым в оптических коммуникационных системах. Прежде чем продолжить рассмотрение распределения электрического поля фундаментальной моды, необходимо понять концепцию поляризации электрического поля, представляющего собой вектор электрического поля‚ размер и направление которого могут изменяться со временем. Изменяющееся со временем электрическое поле считается линейно поляризованным, если его направление является постоянным, т. е. не зависит от времени. Так, если электрическое поле, ассоциируемое с электромагнитной волной, не имеет компоненты вдоль направления распространения волны, электрическое поле считается поперечным, а в противном случае — продольным. Для фундаментальной моды одномодового волокна величина продольной компоненты Е, значительно меньше величины поперечной компоненты Е, или Е у. Поэтому электрическое поле фундаментальной моды с большой долей вероятности является поперечным полем. Учитывая это предположение, два линейно независимых решения волнового уравнения представляют линейно поляризованные вдоль осей 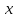 и и 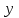  электрические поля, а так как эти два направления перпендикулярны друг другу, решения называются ортогонально поляризованными электрическими полями. Здесь следует отметить, что когда уравнения волны линейны, любая линейная комбинация этих двух линейно поляризованных полей также является решением уравнения и, таким образом, фундаментальной модой. Состояние поляризации (БОР) относится к распределению световой энергии среди двух поляризационных мод. Причина того, что волокно по-прежнему называется одномодовым, заключается в том, что эти две поляризационные моды имеют одну и туже постоянную распространения, по крайней мере, в идеальном, совершенно симметричном волокне. Таким образом, хотя энергия импульса разделяется между этими двумя поляризационными модами, но то, что они имеют одинаковую постоянную распространения, не вызывает расширения импульса вследствие явления дисперсии. В то же время реальное волокно не является совершенно симметричным, и две ортогонально поляризованные моды имеют неидентичные постоянные распространения. Поэтому, учитывая, что световая энергия импульса, распространяющегося по волокну, разделена между этими двумя модами, отличие постоянных распространения этих мод вызывает увеличение длительности импульса на выходе волокна. Это явление носит название поляризационной модовой дисперсии (РМВ), что в принципе аналогично расширению импульса в случае использования многомодового волокна, но в данном случае это явление гораздо слабее. Многие оптические материалы и компоненты, изготовленные с использованием этих материалов, по разному реагируют на различные поляризаций входного излучения. К этим поляризационно-чувствительным компонентам относятся собственно оптическое волокно, изоляторы, циркуляторы, оптико-акустические настраиваемые фильтры и др. электрические поля, а так как эти два направления перпендикулярны друг другу, решения называются ортогонально поляризованными электрическими полями. Здесь следует отметить, что когда уравнения волны линейны, любая линейная комбинация этих двух линейно поляризованных полей также является решением уравнения и, таким образом, фундаментальной модой. Состояние поляризации (БОР) относится к распределению световой энергии среди двух поляризационных мод. Причина того, что волокно по-прежнему называется одномодовым, заключается в том, что эти две поляризационные моды имеют одну и туже постоянную распространения, по крайней мере, в идеальном, совершенно симметричном волокне. Таким образом, хотя энергия импульса разделяется между этими двумя поляризационными модами, но то, что они имеют одинаковую постоянную распространения, не вызывает расширения импульса вследствие явления дисперсии. В то же время реальное волокно не является совершенно симметричным, и две ортогонально поляризованные моды имеют неидентичные постоянные распространения. Поэтому, учитывая, что световая энергия импульса, распространяющегося по волокну, разделена между этими двумя модами, отличие постоянных распространения этих мод вызывает увеличение длительности импульса на выходе волокна. Это явление носит название поляризационной модовой дисперсии (РМВ), что в принципе аналогично расширению импульса в случае использования многомодового волокна, но в данном случае это явление гораздо слабее. Многие оптические материалы и компоненты, изготовленные с использованием этих материалов, по разному реагируют на различные поляризаций входного излучения. К этим поляризационно-чувствительным компонентам относятся собственно оптическое волокно, изоляторы, циркуляторы, оптико-акустические настраиваемые фильтры и др. |
|
|
 Скачать 0.68 Mb.
Скачать 0.68 Mb.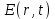 и магнитного
и магнитного 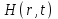 полей в пространстве и времени. Здесь r обозначает положение вектора, а t — время. Иногда более удобно иметь дело с преобразованием Фурье этих векторов, которое для вектора Е определяется следующим образом [4]:
полей в пространстве и времени. Здесь r обозначает положение вектора, а t — время. Иногда более удобно иметь дело с преобразованием Фурье этих векторов, которое для вектора Е определяется следующим образом [4]: 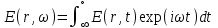 (1.20) Преобразование Фурье для вектора Н и других векторов определяется аналогичным образом. Очевидно, что даже когда Е(r,t) реально, E(r,w) может быть комплексным, несмотря на это, во многих случаях оказывается очень удобным представлять Е(г,1) также в комплексном виде, принимая во внимание только реальную часть полученных решений. Как известно, электроны в атоме заряжены отрицательно, а ядро несет положительный заряд, поэтому, когда электрическое поле прилагается к материалу, подобному кварцу, силы, испытываемые ядрами и электронами, имеют противоположные направления, что приводит к поляризации атомов. индуцированная электрическая поляризация материала, или просто поляризация, может быть описана при помощи вектора ЕР’, который зависит как от особенностей материала, так и прилагаемого поля. индуцированная поляризация может быть рассмотрена как отклик среды на прилагаемое электрическое поле. Рассмотрим связь Р и Е более подробно, определив вначале вектор В, называемый электрической индукцией, который связан с электрическим полем Е и электрической поляризацией Р, следующим образом:
(1.20) Преобразование Фурье для вектора Н и других векторов определяется аналогичным образом. Очевидно, что даже когда Е(r,t) реально, E(r,w) может быть комплексным, несмотря на это, во многих случаях оказывается очень удобным представлять Е(г,1) также в комплексном виде, принимая во внимание только реальную часть полученных решений. Как известно, электроны в атоме заряжены отрицательно, а ядро несет положительный заряд, поэтому, когда электрическое поле прилагается к материалу, подобному кварцу, силы, испытываемые ядрами и электронами, имеют противоположные направления, что приводит к поляризации атомов. индуцированная электрическая поляризация материала, или просто поляризация, может быть описана при помощи вектора ЕР’, который зависит как от особенностей материала, так и прилагаемого поля. индуцированная поляризация может быть рассмотрена как отклик среды на прилагаемое электрическое поле. Рассмотрим связь Р и Е более подробно, определив вначале вектор В, называемый электрической индукцией, который связан с электрическим полем Е и электрической поляризацией Р, следующим образом: 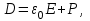 (1.21) где
(1.21) где 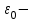 -постоянная, называемая относительной диэлектрической проницаемостью среды, в нашем случае вакуума. Электрическая индукция в вакууме равна . Аналогично определяется связь магнитной поляризации
-постоянная, называемая относительной диэлектрической проницаемостью среды, в нашем случае вакуума. Электрическая индукция в вакууме равна . Аналогично определяется связь магнитной поляризации 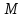 и маг- нитной индукции В
и маг- нитной индукции В 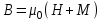 (1.22) Однако, так как кварц является немагнитным материалом,
(1.22) Однако, так как кварц является немагнитным материалом, 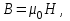 где
где 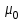 ‚но есть постоянная, называемая магнитной проницаемостью вакума. Таким образом уравнения Максвелла учитывают влияние характеристик материала на распространение электромагнитных волн, так как они используют не только Е и Н, но и электрическую D , и магнитную В индукцию. Связь P и Е в оптическом волокне определяется свойствами среды (кварца) и является причиной двух важных явлений, относящихся к распространению в нем света, — дисперсии и нелинейным эффектам, которые налагают ограничения на функционирование современных коммуникационных систем. Рассмотрим пять фундаментальных характеристик среды и их влияние на связь между индуцированной поляризацией Р в среде и воздействующим электрическим полем Е. Локальность отклика. В среде, отклик которой на прилагаемое электрическое поле является локальным и когда
‚но есть постоянная, называемая магнитной проницаемостью вакума. Таким образом уравнения Максвелла учитывают влияние характеристик материала на распространение электромагнитных волн, так как они используют не только Е и Н, но и электрическую D , и магнитную В индукцию. Связь P и Е в оптическом волокне определяется свойствами среды (кварца) и является причиной двух важных явлений, относящихся к распространению в нем света, — дисперсии и нелинейным эффектам, которые налагают ограничения на функционирование современных коммуникационных систем. Рассмотрим пять фундаментальных характеристик среды и их влияние на связь между индуцированной поляризацией Р в среде и воздействующим электрическим полем Е. Локальность отклика. В среде, отклик которой на прилагаемое электрическое поле является локальным и когда 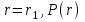 , зависит только от
, зависит только от 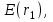 значения Е (r) для
значения Е (r) для 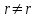 , не оказывают влияния на
, не оказывают влияния на 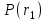 . Это свойство соблюдается с достаточно высокой степенью приближения для кварцевого волокна в диапазоне длин волн от 0.5 мкм до 2 мкм, который и используется в оптических коммуникационных системах. Изотропия. Изотропная среда характеризуется тем, что ее электро-магнитные свойства, такие, как показатель преломления, одинаковы во всех направлениях. В изотропной среде
. Это свойство соблюдается с достаточно высокой степенью приближения для кварцевого волокна в диапазоне длин волн от 0.5 мкм до 2 мкм, который и используется в оптических коммуникационных системах. Изотропия. Изотропная среда характеризуется тем, что ее электро-магнитные свойства, такие, как показатель преломления, одинаковы во всех направлениях. В изотропной среде 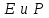 являются векторами одинаковой ориентации, и так как кварц представляет собой изотропную среду, идеально цилиндрическое оптическое волокно также является изотропным. Среда, показатели преломления которой вдоль двух отличных направлений соответствующей системы координат, например вдоль осей х и у, различны, называется двулучепреломляющей, поэтому оптическое волокно, не обладающее цилиндрической симметрией, также называется двулучепреломляющим. Двулучепреломление ряда материалов, таких, как ниобат лития, используется в ряде волоконно-оптических компонентов, таких, как модуляторы, изоляторы и настраиваемые фильтры. Линейность. В линейной изотропной среде
являются векторами одинаковой ориентации, и так как кварц представляет собой изотропную среду, идеально цилиндрическое оптическое волокно также является изотропным. Среда, показатели преломления которой вдоль двух отличных направлений соответствующей системы координат, например вдоль осей х и у, различны, называется двулучепреломляющей, поэтому оптическое волокно, не обладающее цилиндрической симметрией, также называется двулучепреломляющим. Двулучепреломление ряда материалов, таких, как ниобат лития, используется в ряде волоконно-оптических компонентов, таких, как модуляторы, изоляторы и настраиваемые фильтры. Линейность. В линейной изотропной среде 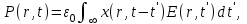 (1.23) где
(1.23) где 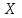 называется чувствительностью, или, более точно, чувствительностью линейной среды. Таким образом, индуцированная поляризация получается путем свертки прилагаемого электрического поля. Если
называется чувствительностью, или, более точно, чувствительностью линейной среды. Таким образом, индуцированная поляризация получается путем свертки прилагаемого электрического поля. Если 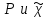 обозначают соответственно преобразования Фурье
обозначают соответственно преобразования Фурье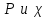 , (1.2З) примет вид
, (1.2З) примет вид 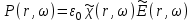 (1.24) В этом случае индуцированная поляризация может рассматриваться как выход линейной системы с входным сигналом
(1.24) В этом случае индуцированная поляризация может рассматриваться как выход линейной системы с входным сигналом 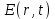 или
или 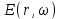 импульсным откликом
импульсным откликом 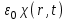 и функцией преобразования
и функцией преобразования 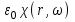 . Таким образом, отклик среды на прилагаемое электрическое поле не является мгновенным, так как
. Таким образом, отклик среды на прилагаемое электрическое поле не является мгновенным, так как 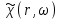 зависит от
зависит от 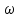 Это является причиной важного эффекта, свойственного распространению света в оптическом волокне, — дисперсии, в данном случае хроматической дисперсии, налагающей основное ограничение на функционирование оптических систем передачи. Таким образом, происхождение хроматической дисперсии кроется в задержке отклика индуцированной поляризации в кварцевой среде на действие прилагаемого электрического поля. Подобное линейное соотношение связи
Это является причиной важного эффекта, свойственного распространению света в оптическом волокне, — дисперсии, в данном случае хроматической дисперсии, налагающей основное ограничение на функционирование оптических систем передачи. Таким образом, происхождение хроматической дисперсии кроется в задержке отклика индуцированной поляризации в кварцевой среде на действие прилагаемого электрического поля. Подобное линейное соотношение связи 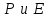 реально не соблюдается для кварца, однако обладает достаточно высокой степенью приближения для сигналов средней мощности и умеренной битовой скорости. Влияние поляризационной модовой дисперсии и нелинейных явлений на распространение света будет дано позже. Однородность. Однородная среда характеризуется тем, что электромагнитные характеристики
реально не соблюдается для кварца, однако обладает достаточно высокой степенью приближения для сигналов средней мощности и умеренной битовой скорости. Влияние поляризационной модовой дисперсии и нелинейных явлений на распространение света будет дано позже. Однородность. Однородная среда характеризуется тем, что электромагнитные характеристики 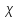 и, соответственно‚
и, соответственно‚ 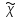 не зависят от положения вектора
не зависят от положения вектора 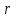 , поэтому
, поэтому 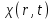 в этом случае можно заменить на
в этом случае можно заменить на 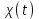 Однако, несмотря на то, что кварц является однородной средой, оптическое волокво неоднородно из-за того, что показатели преломления сердцевины и оболочки различны. Поэтому области сердцевины и оболочки в волокне со ступенчато изменяющимся показателем преломления могут рассматриваться раздельно как однородные среды, в то время как в градиентном волокне это допущение неприемлемо ввиду его неоднородной сердцевины. Отсутствие потерь. Хотя нельзя говорить, что кварцевое волокно функционирует без потерь, при рассмотрении распространения мод потерями можно пренебречь, приравняв их к нулю, так как параметры этих мод не будут существенно изменяться при таком допущении. Таким образом, принятые допущения, заключающиеся в том, что области сердцевины и оболочки кварцевого волокна являются локально чувствительными, изотропными, линейными, однородными и обладают нулевым показателем потерь, соответствуют идеализированному оптическому волокну. В то же время, учитывая, что чувствительность 2 является более фундаментальной характеристикой материала, чем показатель преломления п ‚ выраженный отношением скорости света в вакууме к скорости света в материале волокна, определим последний в терминах чувствительности
Однако, несмотря на то, что кварц является однородной средой, оптическое волокво неоднородно из-за того, что показатели преломления сердцевины и оболочки различны. Поэтому области сердцевины и оболочки в волокне со ступенчато изменяющимся показателем преломления могут рассматриваться раздельно как однородные среды, в то время как в градиентном волокне это допущение неприемлемо ввиду его неоднородной сердцевины. Отсутствие потерь. Хотя нельзя говорить, что кварцевое волокно функционирует без потерь, при рассмотрении распространения мод потерями можно пренебречь, приравняв их к нулю, так как параметры этих мод не будут существенно изменяться при таком допущении. Таким образом, принятые допущения, заключающиеся в том, что области сердцевины и оболочки кварцевого волокна являются локально чувствительными, изотропными, линейными, однородными и обладают нулевым показателем потерь, соответствуют идеализированному оптическому волокну. В то же время, учитывая, что чувствительность 2 является более фундаментальной характеристикой материала, чем показатель преломления п ‚ выраженный отношением скорости света в вакууме к скорости света в материале волокна, определим последний в терминах чувствительности 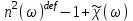 (1.25) и будем рассматривать его как функцию угловой частоты
(1.25) и будем рассматривать его как функцию угловой частоты 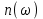 аналогично (1.25). Для волокна со значением
аналогично (1.25). Для волокна со значением 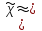 1.25 и показателем преломления
1.25 и показателем преломления 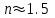 1.1.3.1. Волновые уравнения В общем случае распространение электромагнитных волн описывается системой основных уравнений Максвелла в векторной форме [5]
1.1.3.1. Волновые уравнения В общем случае распространение электромагнитных волн описывается системой основных уравнений Максвелла в векторной форме [5] 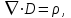 (1.26)
(1.26) 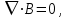 (1.27)
(1.27) 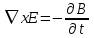 (1.28)
(1.28) 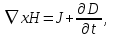 (1.29) где
(1.29) где 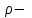 плотность электрического заряда;
плотность электрического заряда; 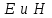 - напряженность электрического и магнитного полей;
- напряженность электрического и магнитного полей; 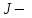 плотность тока;
плотность тока; 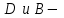 электрическая и магнитная индукции. Таким образом, уравнения Максвелла учитывают влияние характеристик материала на распространение электромагнитных волн, так как в них входит не только
электрическая и магнитная индукции. Таким образом, уравнения Максвелла учитывают влияние характеристик материала на распространение электромагнитных волн, так как в них входит не только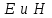 , но и D и B. Предположив, что в среде нет свободных зарядов, т. е.
, но и D и B. Предположив, что в среде нет свободных зарядов, т. е.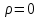 , следовательно,
, следовательно, 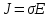 ‚ а так как проводимость кварца очень низка, т. е.
‚ а так как проводимость кварца очень низка, т. е. 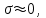 можно заключить, что
можно заключить, что 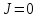 . Тогда, используя (1.21) и (1.22)‚ а также исключив индукцию из уравнений (1.28) и (1.29)‚ представим уравнения Максвелла только в терминах полей
. Тогда, используя (1.21) и (1.22)‚ а также исключив индукцию из уравнений (1.28) и (1.29)‚ представим уравнения Максвелла только в терминах полей 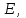
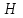 и поляризации P [5]:
и поляризации P [5]: 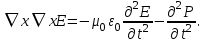 (1.30) Чтобы решить это уравнение относительно Е, необходимо соотнести
(1.30) Чтобы решить это уравнение относительно Е, необходимо соотнести 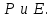 Без учета нелинейных эффектов можно допустить, что связь
Без учета нелинейных эффектов можно допустить, что связь 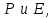 имеет линейный характер, определяемый выражением (1.24), и. более того, вследствие предположения об однородности можно вместо
имеет линейный характер, определяемый выражением (1.24), и. более того, вследствие предположения об однородности можно вместо 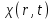 записать
записать 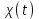 ослабив это предположение при рассмотрении нелинейных явлений. Решить (1.30) относительно
ослабив это предположение при рассмотрении нелинейных явлений. Решить (1.30) относительно 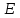 наиболее удобно посредством преобразования Фурье [5], которое для
наиболее удобно посредством преобразования Фурье [5], которое для 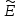 от
от 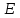 определяется согласно (1.20)‚ а для
определяется согласно (1.20)‚ а для 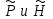 находится аналогичным образом. В результате
находится аналогичным образом. В результате 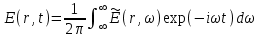 (1.31) Путем дифференцирования этого уравнения относительно
(1.31) Путем дифференцирования этого уравнения относительно 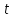 имеем преобразование Фурье для
имеем преобразование Фурье для 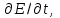 равное -
равное -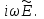 Принимая во внимание преобразование Фурье (1.30), имеем
Принимая во внимание преобразование Фурье (1.30), имеем 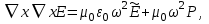 затем, используя (1.24) для выражения
затем, используя (1.24) для выражения 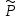
 в терминах
в терминах 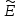 , сведем его до уравнения вида
, сведем его до уравнения вида 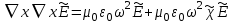 Введем с =1/
Введем с =1/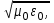 где с — скорость света в вакууме, пренебрегая потерями и принимая
где с — скорость света в вакууме, пренебрегая потерями и принимая 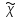 за реальную величину, можно записать
за реальную величину, можно записать 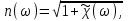 где
где 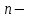 показатель преломления, тогда
показатель преломления, тогда 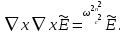 Используя идентичность
Используя идентичность 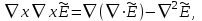 уравнение (1.32) можно преобразовать к виду
уравнение (1.32) можно преобразовать к виду 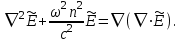 (1.33) Допуская однородность среды (
(1.33) Допуская однородность среды (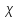 не зависит от
не зависит от 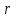 ), а также используя (1.26) и (1.25), имеем
), а также используя (1.26) и (1.25), имеем 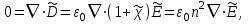 (1.34) что позволяет упростить (1.3З) и получить волновое уравнение для Е в виде
(1.34) что позволяет упростить (1.3З) и получить волновое уравнение для Е в виде 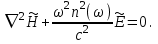 (1.35) Выполняя аналогичные операции, можно вывести волновое уравнение и для
(1.35) Выполняя аналогичные операции, можно вывести волновое уравнение и для 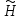 :
: 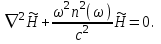 (1.36) Здесь
(1.36) Здесь 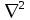 обозначает оператор Лапласа, который определяется в прямоугольной системе координат выражением
обозначает оператор Лапласа, который определяется в прямоугольной системе координат выражением 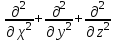 . Таким образом, волновые уравнения представляют собой линейные дифференциальные уравнения в частных производных второго порядка для преобразования Фурье векторов электрического и магнитного поля. На самом деле каждое уравнение волны отражает три уравнения — по одному на каждый компонент вектора соответствующего поля. 1.1.З.2. Поляризация световых волн Как было показано выше, мода распространяемой в волокне световой волны определяется как решение волнового уравнения, которое удовлетворяет граничным условиям на разделе сердцевина — оболочка. При этом имеют место два линейно независимых решения волновых уравнений для всех
. Таким образом, волновые уравнения представляют собой линейные дифференциальные уравнения в частных производных второго порядка для преобразования Фурье векторов электрического и магнитного поля. На самом деле каждое уравнение волны отражает три уравнения — по одному на каждый компонент вектора соответствующего поля. 1.1.З.2. Поляризация световых волн Как было показано выше, мода распространяемой в волокне световой волны определяется как решение волнового уравнения, которое удовлетворяет граничным условиям на разделе сердцевина — оболочка. При этом имеют место два линейно независимых решения волновых уравнений для всех 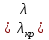 вне зависимости от того, насколько велики их значения. Эти решения соответствуют фундаментальной моде и имеют идентичную постоянную распространения. Другие решения существуют только когда
вне зависимости от того, насколько велики их значения. Эти решения соответствуют фундаментальной моде и имеют идентичную постоянную распространения. Другие решения существуют только когда 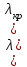 . Рассмотрим поведение фундаментальной моды, представив электрическое поле
. Рассмотрим поведение фундаментальной моды, представив электрическое поле 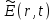 световой волны в виде
световой волны в виде 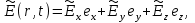 (1‚37) где
(1‚37) где 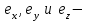 соответственно единичные векторы вдоль осей
соответственно единичные векторы вдоль осей 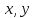 и
и 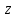 , причем
, причем 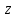 — направление распространения световой волны (ось волокна), а каждое значение
— направление распространения световой волны (ось волокна), а каждое значение 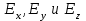 может зависеть в основном от
может зависеть в основном от 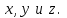 Как показано в [5], данное уравнение имеет два линейно независимых решения (1.35), которые соответствуют фундаментальной моде, при этом одно изрешений соответствует
Как показано в [5], данное уравнение имеет два линейно независимых решения (1.35), которые соответствуют фундаментальной моде, при этом одно изрешений соответствует 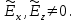 когда
когда 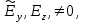 а другое
а другое 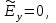 когда
когда 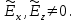 Так как z является также направлением распространения,
Так как z является также направлением распространения, 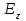 называется продольной компонентой. Другой ненулевой компонент, то есть
называется продольной компонентой. Другой ненулевой компонент, то есть 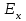 , или
, или 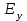 , называется поперечной компонентой. Для фундаментальной моды продольный и поперечный компоненты могут быть представлены в виде
, называется поперечной компонентой. Для фундаментальной моды продольный и поперечный компоненты могут быть представлены в виде 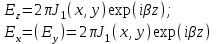 (1.38), (1.39) где .
(1.38), (1.39) где . 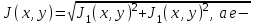 вследствие цилиндрической симметрии волокна являются функцией
вследствие цилиндрической симметрии волокна являются функцией 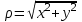 и представляют собой функцию Бесселя. Для определения в частотной области каждого из решений, соответ- ствующего фундаментальной моде, заменим
и представляют собой функцию Бесселя. Для определения в частотной области каждого из решений, соответ- ствующего фундаментальной моде, заменим 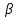 на
на 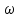 тогда
тогда 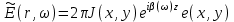 (1.40) где
(1.40) где 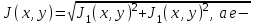 единичный вектор вдоль направления
единичный вектор вдоль направления 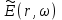 . В общем случае, конечно,
. В общем случае, конечно, 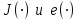 также являются функциями
также являются функциями 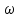 , но этой зависимостью можно пренебречь для импульсов, ширина спектра которых значительно меньше их центральной частоты, что соответствует импульсам, используемым в оптических коммуникационных системах. Прежде чем продолжить рассмотрение распределения электрического поля фундаментальной моды, необходимо понять концепцию поляризации электрического поля, представляющего собой вектор электрического поля‚ размер и направление которого могут изменяться со временем. Изменяющееся со временем электрическое поле считается линейно поляризованным, если его направление является постоянным, т. е. не зависит от времени. Так, если электрическое поле, ассоциируемое с электромагнитной волной, не имеет компоненты вдоль направления распространения волны, электрическое поле считается поперечным, а в противном случае — продольным. Для фундаментальной моды одномодового волокна величина продольной компоненты Е, значительно меньше величины поперечной компоненты Е, или Е у. Поэтому электрическое поле фундаментальной моды с большой долей вероятности является поперечным полем. Учитывая это предположение, два линейно независимых решения волнового уравнения представляют линейно поляризованные вдоль осей
, но этой зависимостью можно пренебречь для импульсов, ширина спектра которых значительно меньше их центральной частоты, что соответствует импульсам, используемым в оптических коммуникационных системах. Прежде чем продолжить рассмотрение распределения электрического поля фундаментальной моды, необходимо понять концепцию поляризации электрического поля, представляющего собой вектор электрического поля‚ размер и направление которого могут изменяться со временем. Изменяющееся со временем электрическое поле считается линейно поляризованным, если его направление является постоянным, т. е. не зависит от времени. Так, если электрическое поле, ассоциируемое с электромагнитной волной, не имеет компоненты вдоль направления распространения волны, электрическое поле считается поперечным, а в противном случае — продольным. Для фундаментальной моды одномодового волокна величина продольной компоненты Е, значительно меньше величины поперечной компоненты Е, или Е у. Поэтому электрическое поле фундаментальной моды с большой долей вероятности является поперечным полем. Учитывая это предположение, два линейно независимых решения волнового уравнения представляют линейно поляризованные вдоль осей 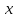 и
и 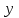
 электрические поля, а так как эти два направления перпендикулярны друг другу, решения называются ортогонально поляризованными электрическими полями. Здесь следует отметить, что когда уравнения волны линейны, любая линейная комбинация этих двух линейно поляризованных полей также является решением уравнения и, таким образом, фундаментальной модой. Состояние поляризации (БОР) относится к распределению световой энергии среди двух поляризационных мод. Причина того, что волокно по-прежнему называется одномодовым, заключается в том, что эти две поляризационные моды имеют одну и туже постоянную распространения, по крайней мере, в идеальном, совершенно симметричном волокне. Таким образом, хотя энергия импульса разделяется между этими двумя поляризационными модами, но то, что они имеют одинаковую постоянную распространения, не вызывает расширения импульса вследствие явления дисперсии. В то же время реальное волокно не является совершенно симметричным, и две ортогонально поляризованные моды имеют неидентичные постоянные распространения. Поэтому, учитывая, что световая энергия импульса, распространяющегося по волокну, разделена между этими двумя модами, отличие постоянных распространения этих мод вызывает увеличение длительности импульса на выходе волокна. Это явление носит название поляризационной модовой дисперсии (РМВ), что в принципе аналогично расширению импульса в случае использования многомодового волокна, но в данном случае это явление гораздо слабее. Многие оптические материалы и компоненты, изготовленные с использованием этих материалов, по разному реагируют на различные поляризаций входного излучения. К этим поляризационно-чувствительным компонентам относятся собственно оптическое волокно, изоляторы, циркуляторы, оптико-акустические настраиваемые фильтры и др.
электрические поля, а так как эти два направления перпендикулярны друг другу, решения называются ортогонально поляризованными электрическими полями. Здесь следует отметить, что когда уравнения волны линейны, любая линейная комбинация этих двух линейно поляризованных полей также является решением уравнения и, таким образом, фундаментальной модой. Состояние поляризации (БОР) относится к распределению световой энергии среди двух поляризационных мод. Причина того, что волокно по-прежнему называется одномодовым, заключается в том, что эти две поляризационные моды имеют одну и туже постоянную распространения, по крайней мере, в идеальном, совершенно симметричном волокне. Таким образом, хотя энергия импульса разделяется между этими двумя поляризационными модами, но то, что они имеют одинаковую постоянную распространения, не вызывает расширения импульса вследствие явления дисперсии. В то же время реальное волокно не является совершенно симметричным, и две ортогонально поляризованные моды имеют неидентичные постоянные распространения. Поэтому, учитывая, что световая энергия импульса, распространяющегося по волокну, разделена между этими двумя модами, отличие постоянных распространения этих мод вызывает увеличение длительности импульса на выходе волокна. Это явление носит название поляризационной модовой дисперсии (РМВ), что в принципе аналогично расширению импульса в случае использования многомодового волокна, но в данном случае это явление гораздо слабее. Многие оптические материалы и компоненты, изготовленные с использованием этих материалов, по разному реагируют на различные поляризаций входного излучения. К этим поляризационно-чувствительным компонентам относятся собственно оптическое волокно, изоляторы, циркуляторы, оптико-акустические настраиваемые фильтры и др. 