|
|
ВОЛС. Оптическое волокно Сандугаш. Волоконнооптические
1.1.10. Преобразование поляризации Для анализа изменения состояния поляризаций оптического сигнала при его прохождении через оптические вещества и компоненты часто пользуется аналитическим представлением световой волны с помощью вектора Джонса, отражающего ее геометрическую, амплитудную и фазовую характеристики, при одновременном описании поляризационных характеристик оптического компонента одноименной матрицей. Это позволяет проводить анализ оптической цепи аналогично хорошо разработанным методом анализа электричеких цепей. Ниже приводится описание описание электрических полей оптического сигнала вектором Джонса [8], где для наглядности временная компонента сигнала опущена. Так, для электрических полей 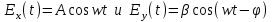 (1.69) Вектор Джонса имеет вид (1.69) Вектор Джонса имеет вид  (1.70) Если имеет место линейная поляризация, векторы Еx и Еy синхронизированы и (1.70) Если имеет место линейная поляризация, векторы Еx и Еy синхронизированы и  а при круговой поляризации с задержкой а при круговой поляризации с задержкой 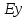 относительно Еx на 90° вектор Джонса примет вид относительно Еx на 90° вектор Джонса примет вид 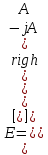 Электрическое поле Е2 оптического сигнала на выходе оптического компонента согласно методу Джонса определяется произведением матрицы Джонса J на вектор Джонса Е1 входного сигнала, т. е. Электрическое поле Е2 оптического сигнала на выходе оптического компонента согласно методу Джонса определяется произведением матрицы Джонса J на вектор Джонса Е1 входного сигнала, т. е. 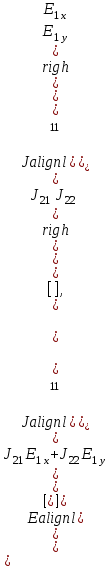 (1.71) В качестве примера рассмотрим четвертьволновую пластину, у которой быстрая ось кристалла ориентирована параллельно направлению х. Соответствующая этому случаю матрица Джонса имеет вид (1.71) В качестве примера рассмотрим четвертьволновую пластину, у которой быстрая ось кристалла ориентирована параллельно направлению х. Соответствующая этому случаю матрица Джонса имеет вид 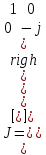 Теперь определим выходные сигналы четвертьволновой пластины при различных состояниях поляризации входного сигнала Е1‚ выполнив умножение матрицы J на соответствующее Е1. Пусть входное излучение линейно поляризовапо вдоль направления у , а Y компонента Е2 задерживается по фазе на 90°, когда х компонента все еще равна нулю. Это означает, что E2 все еще имеет линейную поляризацию в направлении у , поэтому Теперь определим выходные сигналы четвертьволновой пластины при различных состояниях поляризации входного сигнала Е1‚ выполнив умножение матрицы J на соответствующее Е1. Пусть входное излучение линейно поляризовапо вдоль направления у , а Y компонента Е2 задерживается по фазе на 90°, когда х компонента все еще равна нулю. Это означает, что E2 все еще имеет линейную поляризацию в направлении у , поэтому 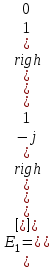 Теперь предположим, что входной сигнал линейно поляризован под углом в Теперь предположим, что входной сигнал линейно поляризован под углом в 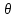 =45°. Тогда х компонента Е, по-прежнему равна 1, а у компонента задерживается на 90°, что соответствует круговому состоянию поляризации с направлением вращения против часовой стрелки: =45°. Тогда х компонента Е, по-прежнему равна 1, а у компонента задерживается на 90°, что соответствует круговому состоянию поляризации с направлением вращения против часовой стрелки: 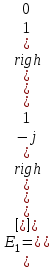 И, наконец, когда на входе сигнал имеет круговую поляризацию, обе компоненты Е2 - х и у — равны 1, что соответствует сигналу, линейно поляризованному под углом И, наконец, когда на входе сигнал имеет круговую поляризацию, обе компоненты Е2 - х и у — равны 1, что соответствует сигналу, линейно поляризованному под углом 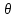 = 45°, т. е. Отсюда видны особенности четвертьволновой пластины, позволяющей выполнять преобразования линейно поляризованных сигналов в сигналы с эллиптической или круговой поляризацией или наоборот. Ниже приведены матрицы Джонса наиболее важных оптических компонентов. Обычная замедляющая пластина характеризуется быстрой (ориентированной в направлении в к поперечному сечению) и медленной осью, поэтому фазовая задержка при распространении сигнала вдоль медленной оси относительно быстрой будет равна = 45°, т. е. Отсюда видны особенности четвертьволновой пластины, позволяющей выполнять преобразования линейно поляризованных сигналов в сигналы с эллиптической или круговой поляризацией или наоборот. Ниже приведены матрицы Джонса наиболее важных оптических компонентов. Обычная замедляющая пластина характеризуется быстрой (ориентированной в направлении в к поперечному сечению) и медленной осью, поэтому фазовая задержка при распространении сигнала вдоль медленной оси относительно быстрой будет равна 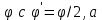 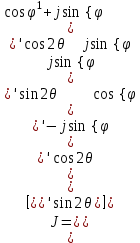 (1.72) Четвертьволновая пластина является частным случаем замедляющей пластины с матрицами Джонса, зависящими от расположения быстрой оси пластины, в частности, когда: быстрая ось установлена в направлении х (1.72) Четвертьволновая пластина является частным случаем замедляющей пластины с матрицами Джонса, зависящими от расположения быстрой оси пластины, в частности, когда: быстрая ось установлена в направлении х 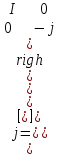 (1.73) (1.73) 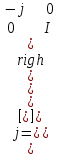 (1.74) Полуволновая пластина — это еще одна разновидность замедляющей пластины, в которой фазовая задержка составляет 180”. В случае, когда входной сигнал линейно поляризован, (1.74) Полуволновая пластина — это еще одна разновидность замедляющей пластины, в которой фазовая задержка составляет 180”. В случае, когда входной сигнал линейно поляризован, 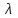 /2- пластина способна поворачивать плоскость поляризации в зависимости от угла между плоскостью поляризации и быстрой осью пластины. Для быстрой оси в направлении /2- пластина способна поворачивать плоскость поляризации в зависимости от угла между плоскостью поляризации и быстрой осью пластины. Для быстрой оси в направлении 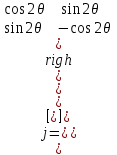 (1.75) Вращатель в отличие от полуволновой пластины поворачивает плоскость поляризации вне зависимости от ориентации поля входного сигнала. Подобное поведение характерно для кругового Двулучепреломления. Угол вращения определяется значением 20 ‚ отсчитываемым по направлению часовой стрелки: (1.75) Вращатель в отличие от полуволновой пластины поворачивает плоскость поляризации вне зависимости от ориентации поля входного сигнала. Подобное поведение характерно для кругового Двулучепреломления. Угол вращения определяется значением 20 ‚ отсчитываемым по направлению часовой стрелки: 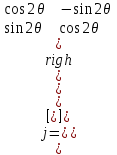 (1.76) Поляризатор является оптическим элементом, который идеальном случае обеспечивает на выходе составляющие электрического поля, ориентированные только вдоль основной оси поляризатора (1.76) Поляризатор является оптическим элементом, который идеальном случае обеспечивает на выходе составляющие электрического поля, ориентированные только вдоль основной оси поляризатора 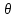 . . 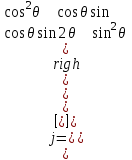 Последовательное соединение двух и более компонентов может моделироваться посредством умножения их матриц. Обозначим матрицы Джонса некоторых компонентов через J и К, а результирующую матрицу L. Тогда L должна определяться в обратном порядке, т. е. L = К x J ‚ а не L, поэтому в общем виде при Последовательное соединение двух и более компонентов может моделироваться посредством умножения их матриц. Обозначим матрицы Джонса некоторых компонентов через J и К, а результирующую матрицу L. Тогда L должна определяться в обратном порядке, т. е. L = К x J ‚ а не L, поэтому в общем виде при |
|
|
 Скачать 0.68 Mb.
Скачать 0.68 Mb.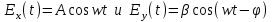 (1.69) Вектор Джонса имеет вид
(1.69) Вектор Джонса имеет вид 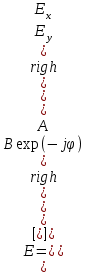 (1.70) Если имеет место линейная поляризация, векторы Еx и Еy синхронизированы и
(1.70) Если имеет место линейная поляризация, векторы Еx и Еy синхронизированы и 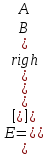 а при круговой поляризации с задержкой
а при круговой поляризации с задержкой 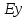 относительно Еx на 90° вектор Джонса примет вид
относительно Еx на 90° вектор Джонса примет вид 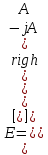 Электрическое поле Е2 оптического сигнала на выходе оптического компонента согласно методу Джонса определяется произведением матрицы Джонса J на вектор Джонса Е1 входного сигнала, т. е.
Электрическое поле Е2 оптического сигнала на выходе оптического компонента согласно методу Джонса определяется произведением матрицы Джонса J на вектор Джонса Е1 входного сигнала, т. е. 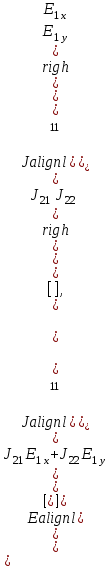 (1.71) В качестве примера рассмотрим четвертьволновую пластину, у которой быстрая ось кристалла ориентирована параллельно направлению х. Соответствующая этому случаю матрица Джонса имеет вид
(1.71) В качестве примера рассмотрим четвертьволновую пластину, у которой быстрая ось кристалла ориентирована параллельно направлению х. Соответствующая этому случаю матрица Джонса имеет вид 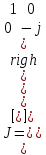 Теперь определим выходные сигналы четвертьволновой пластины при различных состояниях поляризации входного сигнала Е1‚ выполнив умножение матрицы J на соответствующее Е1. Пусть входное излучение линейно поляризовапо вдоль направления у , а Y компонента Е2 задерживается по фазе на 90°, когда х компонента все еще равна нулю. Это означает, что E2 все еще имеет линейную поляризацию в направлении у , поэтому
Теперь определим выходные сигналы четвертьволновой пластины при различных состояниях поляризации входного сигнала Е1‚ выполнив умножение матрицы J на соответствующее Е1. Пусть входное излучение линейно поляризовапо вдоль направления у , а Y компонента Е2 задерживается по фазе на 90°, когда х компонента все еще равна нулю. Это означает, что E2 все еще имеет линейную поляризацию в направлении у , поэтому 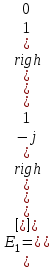 Теперь предположим, что входной сигнал линейно поляризован под углом в
Теперь предположим, что входной сигнал линейно поляризован под углом в 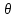 =45°. Тогда х компонента Е, по-прежнему равна 1, а у компонента задерживается на 90°, что соответствует круговому состоянию поляризации с направлением вращения против часовой стрелки:
=45°. Тогда х компонента Е, по-прежнему равна 1, а у компонента задерживается на 90°, что соответствует круговому состоянию поляризации с направлением вращения против часовой стрелки: 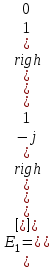 И, наконец, когда на входе сигнал имеет круговую поляризацию, обе компоненты Е2 - х и у — равны 1, что соответствует сигналу, линейно поляризованному под углом
И, наконец, когда на входе сигнал имеет круговую поляризацию, обе компоненты Е2 - х и у — равны 1, что соответствует сигналу, линейно поляризованному под углом 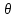 = 45°, т. е. Отсюда видны особенности четвертьволновой пластины, позволяющей выполнять преобразования линейно поляризованных сигналов в сигналы с эллиптической или круговой поляризацией или наоборот. Ниже приведены матрицы Джонса наиболее важных оптических компонентов. Обычная замедляющая пластина характеризуется быстрой (ориентированной в направлении в к поперечному сечению) и медленной осью, поэтому фазовая задержка при распространении сигнала вдоль медленной оси относительно быстрой будет равна
= 45°, т. е. Отсюда видны особенности четвертьволновой пластины, позволяющей выполнять преобразования линейно поляризованных сигналов в сигналы с эллиптической или круговой поляризацией или наоборот. Ниже приведены матрицы Джонса наиболее важных оптических компонентов. Обычная замедляющая пластина характеризуется быстрой (ориентированной в направлении в к поперечному сечению) и медленной осью, поэтому фазовая задержка при распространении сигнала вдоль медленной оси относительно быстрой будет равна 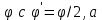
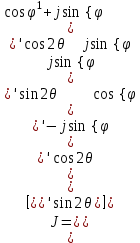 (1.72) Четвертьволновая пластина является частным случаем замедляющей пластины с матрицами Джонса, зависящими от расположения быстрой оси пластины, в частности, когда: быстрая ось установлена в направлении х
(1.72) Четвертьволновая пластина является частным случаем замедляющей пластины с матрицами Джонса, зависящими от расположения быстрой оси пластины, в частности, когда: быстрая ось установлена в направлении х 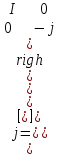 (1.73)
(1.73) 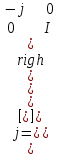 (1.74) Полуволновая пластина — это еще одна разновидность замедляющей пластины, в которой фазовая задержка составляет 180”. В случае, когда входной сигнал линейно поляризован,
(1.74) Полуволновая пластина — это еще одна разновидность замедляющей пластины, в которой фазовая задержка составляет 180”. В случае, когда входной сигнал линейно поляризован, 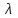 /2- пластина способна поворачивать плоскость поляризации в зависимости от угла между плоскостью поляризации и быстрой осью пластины. Для быстрой оси в направлении
/2- пластина способна поворачивать плоскость поляризации в зависимости от угла между плоскостью поляризации и быстрой осью пластины. Для быстрой оси в направлении 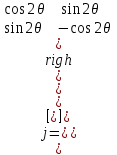 (1.75) Вращатель в отличие от полуволновой пластины поворачивает плоскость поляризации вне зависимости от ориентации поля входного сигнала. Подобное поведение характерно для кругового Двулучепреломления. Угол вращения определяется значением 20 ‚ отсчитываемым по направлению часовой стрелки:
(1.75) Вращатель в отличие от полуволновой пластины поворачивает плоскость поляризации вне зависимости от ориентации поля входного сигнала. Подобное поведение характерно для кругового Двулучепреломления. Угол вращения определяется значением 20 ‚ отсчитываемым по направлению часовой стрелки: 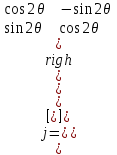 (1.76) Поляризатор является оптическим элементом, который идеальном случае обеспечивает на выходе составляющие электрического поля, ориентированные только вдоль основной оси поляризатора
(1.76) Поляризатор является оптическим элементом, который идеальном случае обеспечивает на выходе составляющие электрического поля, ориентированные только вдоль основной оси поляризатора 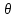 .
. 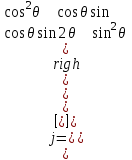 Последовательное соединение двух и более компонентов может моделироваться посредством умножения их матриц. Обозначим матрицы Джонса некоторых компонентов через J и К, а результирующую матрицу L. Тогда L должна определяться в обратном порядке, т. е. L = К x J ‚ а не L, поэтому в общем виде при
Последовательное соединение двух и более компонентов может моделироваться посредством умножения их матриц. Обозначим матрицы Джонса некоторых компонентов через J и К, а результирующую матрицу L. Тогда L должна определяться в обратном порядке, т. е. L = К x J ‚ а не L, поэтому в общем виде при