Ответы на вопросы к экзамену по математике (шпаргалки). Вопрос 1 Матрицы и многомерные векторы
 Скачать 0.91 Mb.
|
|
Вопрос №22 Прямая на плоскости. Через две точки проходит единственная прямая и через точку, лежащую на данной прямой, можно провести единственную прямую, перпендикулярную данной Различные формы уравнения прямой. Уравнение прямой на плоскости. Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно, т.е. А2 + В2 ≠ 0. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи: - C = 0, А ≠ 0, В ≠ 0 – прямая проходит через начало координат - А = 0, В ≠ 0, С ≠ 0 { By + C = 0}- прямая параллельна оси Ох - В = 0, А ≠ 0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу - В = С = 0, А ≠ 0 – прямая совпадает с осью Оу - А = С = 0, В ≠ 0 – прямая совпадает с осью Ох Уравнение прямой по точке и вектору нормали. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0. Уравнение прямой, проходящей через две точки. Пусть в пространстве заданы две точки M1(x1, y1, z1) и M2(x2, y2, z2), тогда уравнение прямой, проходящей через эти точки:  .Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. На плоскости записанное выше уравнение прямой упрощается:  если х1 ≠ х2 и х = х1, если х1 = х2. Дробь  = k называется угловым коэффициентом прямой.Уравнение прямой по точке и угловому коэффициенту. Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:  и обозначить  , то полученное уравнение называется уравнением прямой с угловым коэффициентом k.Уравнение прямой по точке и направляющему вектору. Каждый ненулевой вектор  (a1, a2), компоненты которого удовлетворяют условию Аa1 + Вa2 = 0 называется направляющим вектором прямой Ах + Ву + С = 0.Нормальное уравнение прямой. сли обе части уравнения Ах + Ву + С = 0 разделить на число  , которое называется нормирующем множителем, то получим xcosj + ysinj - p = 0 – нормальное уравнение прямой.Вопрос №23 Угол между прямыми на плоскости. Условие параллельности и перпендикулярности прямых. Определение. Если заданы две прямые y = k1x + b1, y = k2x + b2, то острый угол между этими прямыми будет определяться как  . Две прямые параллельны, если k1 = k2. Две прямые перпендикулярны, если k1 = -1/k2. Теорема. Прямые Ах + Ву + С = 0 и А1х + В1у + С1 = 0 параллельны, когда пропорциональны коэффициенты А1 = lА, В1 = lВ. Если еще и С1 = lС, то прямые совпадают. Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых. Вопрос №24 Различные виды уравнений плоскости в пространстве. У 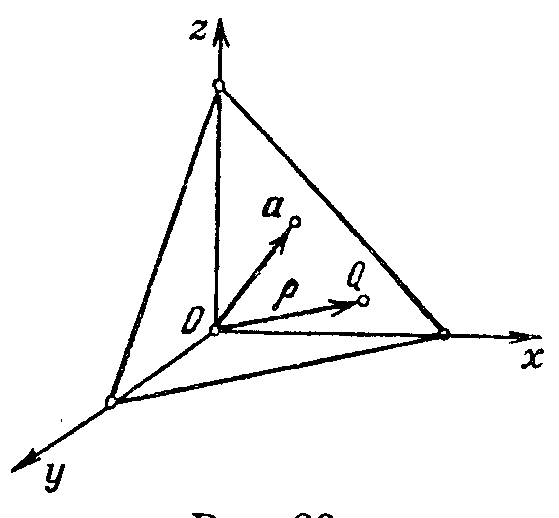 равнение плоскости в нормальном виде. В пространстве R3, где введена прямоугольная система координат x, y, z, зададим вектор а, выпущенный из начала О. Через конец а проведем плоскость П перпендикулярно к а. Произвольную (текущую) точку плоскости П обозначим через Q = (x,y,z). Буква р обозначает радиус-вектор точки Q.Пусть р = |a| - длина вектора а и V = (cos£, cosß, cosγ) – единичный вектор, направленный в ту же сторону что и а. Здесь £, ß, γ – углы, образуемые вектором V соответственно с положительными направлениями осей x,y,z. Проекция любой точки Q Є П на вектор V есть, очевидно, величина постоянная, равная p: (p,V) = p(p>=0) (1). Уравнение (1) имеет смысл и при р=0. В этом случае плоскость П проходит через начало координат О (а=0) и V – единичный вектор, выпущенный из О перпендикулярно к П, неважно в каком направлении, т.е. вектор V определяется с точностью до знака. Уравнение (1) есть уравнение плоскости П в векторной форме. В координатах оно записывается так: xcos£+ycosß+zcosγ=p (p>=0) (1’) и называется уравнением плоскости в нормальном виде. Уравнение плоскости в общем виде. Если уравнение (1’) умножить на какое-либо не равное 0 число, то получим эквивалентное ему уравнение в виде: Ax+By+Cz+D=0 (2), определяющую ту же плоскость. Здесь числа А,В,С не равны нулю одновременно. Уравнение (2), где числа А,В,С не равны нулю, называется уравнение плоскости в общем виде. Уравнение плоскости в отрезках. Если числа A,B,C,D не равны 0, то уравнение (2) можно записать так: x\a+y\b+z\c=1 где а=-D\A, b=-D\B, c=-D\c. Уравнение плоскости, проходящее через точку. Если точка (x0, y0, z0) лежит на плоскости (2), то ее координаты удовлетворяют уравнению (2): Аx0+By0+Cz0+D=0 (3). Вычитая (3) из (2), получим: A(x-x0)+B(y-y0)+C(z-z0)=0. Вопрос №25 Различные виды уравнений прямой в пространстве. Общие уравнения прямой в пространстве.Линия в трехмерном пространстве определяется, вообще говоря, пересечением двух поверхностей, т.е. описывается системой двух уравнений. Прямую в пространстве можно рассматривать как линию пересечения двух плоскостей и, следовательно, описывать системой двух линейных уравнений: A1x + B1y + C1z + D1 = 0 A2x + B2y + C2z + D2 = 0 при условии, что эти плоскости непараллельные, т.е. их нормальные векторы неколлинеарны. Эта система уравнений называется общими уравнениями прямой в пространстве. Каноническое. ((x-x0)\a1)=((y-y0)\a2)=((z-z0)\a3). Параметрическое. Система: (x=x0+a1*t) (y=y0+a2*t) (z=z0+a3*t) Вопрос №26 Взаимное расположение прямых и плоскостей. Плоскость в пространстве определяется точкой и нормальным вектором. Прямая в пространстве определяется точкой и направляющим вектором. Поэтому при решении задач на взаимное расположение прямой и плоскости надо использовать операции с геометрическими векторами, условия ортогональности и коллинеарности векторов. Для нахождения точки пересечения прямой и плоскости надо решить систему трех уравнений с тремя неизвестными (2 уравнения прямой и 1 уравнение плоскости) или использовать параметрические уравнения прямой. Вопрос №27 Расстояние от точки до прямой на плоскости и от точки до плоскости в пространстве. Расстояние от точки до прямой. Теорема. Если задана точка М(х0, у0), то расстояние до прямой Ах + Ву + С =0 определяется как  .Доказательство. Пусть точка М1(х1, у1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М1:  (1). Координаты x1 и у1 могут быть найдены как решение системы уравнений:  . Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М0 перпендикулярно заданной прямой. Если преобразовать первое уравнение системы к виду: A(x – x0) + B(y – y0) + Ax0 + By0 + C = 0, то, решая, получим:  . Подставляя эти выражения в уравнение (1), находим:  .Расстояние от точки до плоскости.   .Вопрос №28 Угол между двумя прямыми в пространстве. Пусть в пространстве заданы две прямые. Их параметрические уравнения: l1:  , l2:  . . Угол между прямыми j и угол между направляющими векторами j этих прямых связаны соотношением: j = j1 или j = 1800 - j1. Угол между направляющими векторами находится из скалярного произведения. Таким образом:  .Условия параллельности и перпендикулярности в пространстве. Условия параллельности и перпендикулярности плоскостей. Для того, чтобы плоскости были перпендикулярны необходимо и достаточно, чтобы косинус угла между плоскостями равнялся нулю. Это условие выполняется, если:  . Плоскости параллельны, векторы нормалей коллинеарны:  || .Это условие выполняется, если: A1\A2=B1\B2=C1\C2. Условия параллельности и перпендикулярности прямых в пространстве. Чтобы две прямые были параллельны необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, т.е. их соответствующие координаты были пропорциональны.  Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю.  .Условия параллельности и перпендикулярности прямой и плоскости в пространстве. Для того, чтобы прямая и плоскость были параллельны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были перпендикулярны. Для этого необходимо, чтобы их скалярное произведение было равно нулю.  . Для того, чтобы прямая и плоскость были перпендикулярны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были коллинеарные. Это условие выполняется, если векторное произведение этих векторов было равно нулю.  .Вопрос №29 О 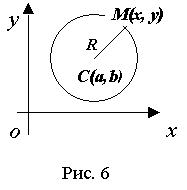 кружность. Окружностью называется геометрическое место точек, равноудаленных от точки, называемой центром окружности.Пусть центр окружности находится в точке С(а, b). Т.к. окружность есть множество точек М(х, у), находящихся на расстоянии R (радиус окружности) от центра С(а, b), то  , то есть  (1). Уравнение (1) и есть уравнение окружности с центром в точке С(а, b) и радиусом R. Если центр окружности находится в начале координат, то ее уравнение примет вид:  .Эллипс. Эллипс есть геометрическое место точек, сумма расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная (большая, чем расстояние между фокусами).  - каноническое уравнение эллипса.Форма. Из канонического уравнения понятно, что оси координат Ох и Оу являются осями симметрии эллипса и, следовательно, начало координат является центром симметрии эллипса. Р 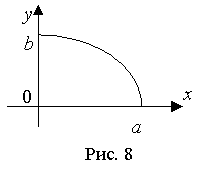 ассмотрим часть эллипса, расположенную в первой четверти, для которой можем записать каноническое уравнение в виде:  .Отсюда видно, что если x = 0, то y = b и, далее, с ростом х значения у убывают. Когда x = a, то y = 0. Числа а и b называют полуосями эллипса. Учитывая симметрию эллипса относительно осей координат, можем построить полный эллипс. Если изменяется величина с, то меняется форма эллипса, а именно: если 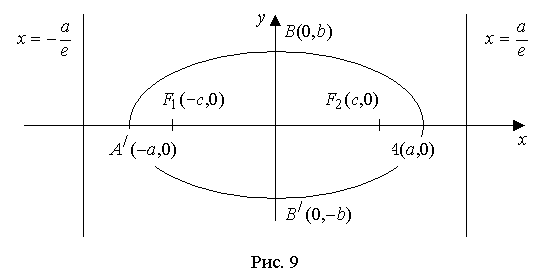  и при c = 0 эллипс становится окружностью с уравнением  . Т.о., окружность есть частный случай эллипса, когда полуоси эллипса равны между собой.Если же с->a, то  , т.е. эллипс сжимается вдоль оси Оу. Величина c\a может служить числовой характеристикой сжатия эллипса.Число  называют эксцентриситетом эллипса. Две прямые  называются директрисами эллипса. Точки пересечения эллипса с осями симметрии  называют вершинами эллипса.Вопрос №30 Гипербола есть геометрическое место точек, абсолютное значение разности расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная (не равная нулю и меньшая, чем расстояние между фокусами. 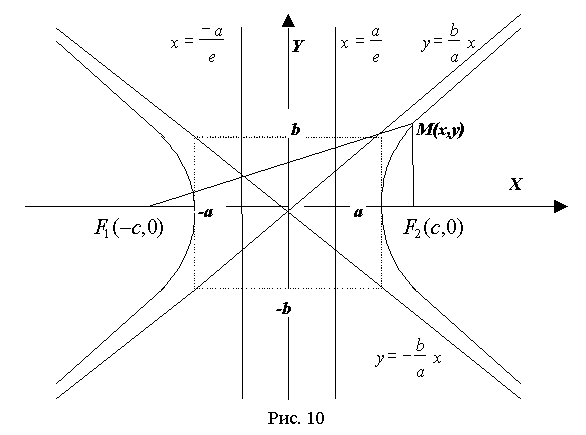  - каноническое уравнение гиперболы.Число а называют действительной полуосью Число а называют действительной полуосью гиперболы, число b - мнимой полуосью. Кривая состоит из двух отдельных частей - ветвей гиперболы, лежащих в областях  .Можно показать, что при  ветви гиперболы неограниченно приближаются к прямым  , не пересекая этих прямых. Эти две прямые называются асимптотами гиперболы. Число  , количественно характеризующее сжатие ветвей гиперболы, называют эксцентриситетом гиперболы. Точки пересечения гиперболы с действительной осью называются вершинами гиперболы. Две прямые  называют директрисами гиперболы. Директрисы гиперболы параллельны оси Оу и пересекают ось Ох между вершинами гиперболы. Вопрос №31 П 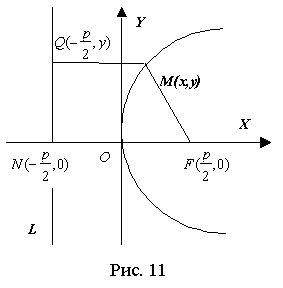 арабола есть геометрическое место точек, для каждой из которых расстояние от некоторой фиксированной точки, называемой фокусом, равно расстоянию до некоторой прямой, называемой директрисой(директриса не проходит через фокус). - каноническое уравнение параболы.Значение р называют параметром параболы.  |