Ответы на вопросы к экзамену по математике (шпаргалки). Вопрос 1 Матрицы и многомерные векторы
 Скачать 0.91 Mb.
|
|
Векторы и линейные операции над ними. Линейными операциями над векторами называется сложение и умножение на число. Суммой двух векторов a и b называется вектор c, направленный из начала вектора a в конец вектора b при условии, что начало b совпадет с концом вектора a. Если векторы заданы их разложениями по базисным ортам, то при сложении векторов складываются их соответствующие координаты. Сумма любого конечного числа векторов может быть найдена по правилу многоугольника: чтобы построить сумму конечного числа векторов, достаточно совместить начало каждого последующего вектора с концом предыдущего и построить вектор, соединяющий начало первого вектора с концом последнего. Разностью векторов a и b называют вектор a+(-b). Второе слагаемое является вектором, противоположным вектору b по направлению, но равным ему по длине. Длина вектора. Длиной (модулем) вектора называется расстояние между началом и концом вектора. Вопрос №13 Координаты на прямой. Упорядоченная тройка некомпланарных векторов e1, e2, e3 называется базисом в множестве всех геометрических векторов. Всякий геометрический вектор a может быть единственным образом представлен в виде a=x1e1+x2e2+x3e3 числа x1 , x2 , x3 называют координатами вектора а в базисе (e1, e2, e3). Деление отрезка в данном отношении  . В координатах:на прямой  ; на плоскости ,  ; в пространстве , ,  .Вопрос №14 Декартовы прямоугольные координаты на плоскости и в пространстве. Системы координат на плоскости. Д 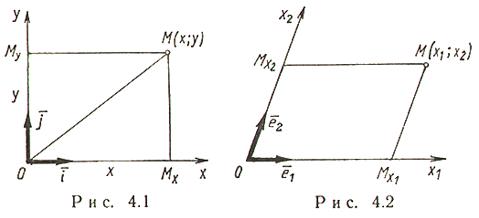 екартовы прямоугольные координаты (рис. 4.1). О - начало координат, Ох - ось абсцисс, Оy - ось ординат,  - базисные векторы,  - абсцисса точки M ( - проекция точки M на ось Ох параллельно оси Оy),  - ордината точки M ( - проекция точки M на ось Oy параллельно оси Ox).Системы координат в пространстве. 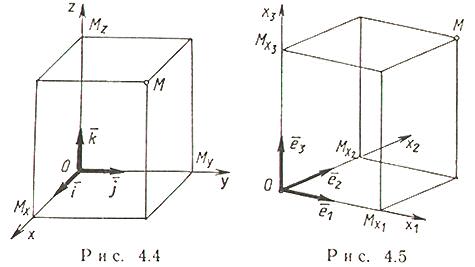Д  екартовы прямоугольные координаты (рис. 4.4). О - начало координат, Ох - ось абсцисс, Оy - ось ординат, Оz - ось аппликат  , - базисные векторы. 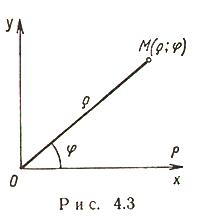Oxy, Oxz, Oyz - координатные плоскости, - абсцисса точки M ( - проекция точки M на ось Ох параллельно плоскости Оyz), - ордината точки M ( - проекция точки M на ось Oy параллельно плоскости Oxz),  - ордината точки M ( - проекция точки M на ось Oz параллельно плоскости Oxy).Вопрос №15 П  олярные координаты на плоскости. О - полюс, Ox - полярная ось,  - полярный радиус,  - полярный угол. Главные значения  и :  (иногда  ).Выражение декартовых прямоугольных координат через полярные:   Выражение полярных координат через декартовы прямоугольные:  С 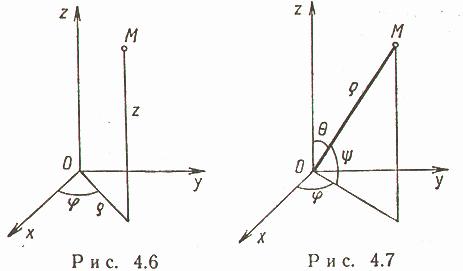 ферические и цилиндрические координаты в пространстве. Цилиндрические координаты. Главные значения , ,  :  Связь между декартовыми прямоугольными и цилиндрическими координатами:  С ферические координаты. Главные значения , ,  :  Иногда вместо рассматривают  :  Вопрос №16 Проекции векторов. Обозначения:  - п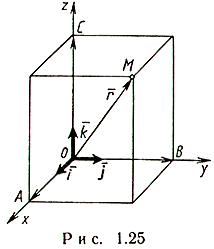роекции вектора  на ось l;  - величина проекции вектора на ось l. Свойства проекций:     С  оставляющие (компоненты) вектора  :     Координаты вектора :    ( - углы, образуемые вектором с положительными направлениями осей координат Ox, Oy, Oz прямоугольной декартовой системы координат).
Вопрос №17 Линейная зависимость векторов. Векторы  называются линейно зависимыми, если существует такая линейная комбинация  , при не равных нулю одновременно ai, т.е.  . Если же только при ai = 0 выполняется , то векторы называются линейно независимыми. Свойство 1. Если среди векторов есть нулевой вектор, то эти векторы линейно зависимы. Свойство 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима. Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов. Свойство 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны. Свойство 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны. Свойство 6. Любые 4 вектора линейно зависимы. Условия коллинеарности, ортогональности и компланарности векторов. Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными. Векторы называются ортогональными, если их скалярное произведение равно нулю. Векторы, лежащие в одной плоскости или параллельные одной плоскости, называются компланарными. Вопрос №18 Преобразование декартовой прямоугольной системы координат на плоскости. Параллельный сдвиг координатных осей. 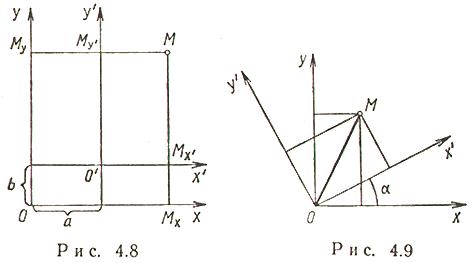  П оворот координатных осей. Параллельный сдвиг и поворот координат осей. 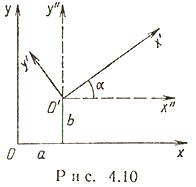  Вопрос №19 Скалярное произведение и его свойства. Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними, т.е.  Из определения следует  где φ - угол между векторами. Скалярная величина  называется проекцией вектора  на вектор  .В зависимости от значения угла между векторами, проекция может принимать отрицательные, положительные или нулевое значения. Теперь можно написать  . Из определения скалярного произведения следует, что если векторы ортогональны, то  (условие ортогональности ненулевых векторов).Свойства скалярного произведения.  Вопрос №20 Векторное произведение векторов. У 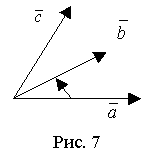 порядоченная тройка векторов  называется правой, если наблюдателю, находящемуся на конце вектора, кратчайший поворот от к кажется происходящим против часовой стрелки. В противном случае тройка векторов левая.Векторным произведением вектора на вектор называется третий вектор  , определяемый следующим образом:1) длина его равна площади параллелограмма, построенного на векторах и , т.е.  где φ - угол между векторами и ;2) вектор  перпендикулярен векторам и ;3) векторы после приведения к общему началу образуют правую тройку векторов.Свойства векторного произведения  Вопрос №21 Смешанное произведение векторов. Смешанным произведением трех векторов называется число  Модуль смешанного произведения трех векторов численно равен объему параллелепипеда, построенного на этих векторах. П 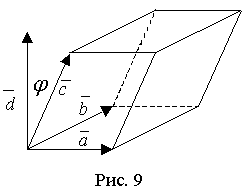 усть правая тройка векторов. Действительно, объем параллелепипеда, построенного на векторах , равен площади основания  на высоту  . Здесь φ - угол между векторами  и .Знак смешанного произведения совпадает со знаком cosφ, и поэтому смешанное произведение положительно, когда тройка векторов правая, и отрицательно, если тройка векторов левая. Если перемножаемые векторы лежат в одной плоскости (cosφ = 0), то  - необходимое и достаточное условие компланарности векторов.Пусть векторы заданы своими разложениями по ортам в декартовой системе координат  .Известно, что  . Скалярно умножим этот вектор на вектор и, учитывая свойства скалярного произведения, получим  Это выражение может быть получено при вычислении определ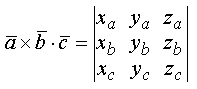ителя  по элементам третьей строки, исходя из правила вычисления определителя.  Поэтому смешанное произведение трех векторов обозначают как , не подчеркивая при этом, какая пара векторов умножается векторно. |
, 
называются направляющими косинусами вектора 
где 
Если 
- единичный вектор в направлении 