шифр 50. Вопрос 10 Понятие функциональной и корреляционной зависимостей между факторами и результатами производства. Границы применения производственных функций
 Скачать 31.78 Kb. Скачать 31.78 Kb.
|
1 2 Вопрос 10 Понятие функциональной и корреляционной зависимостей между факторами и результатами производства. Границы применения производственных функций Различают два типа зависимости между явлениями и их признаками: функциональную, или жестко детерминированную (например, зависимость выработки продукции на одного рабочего от объема выпущенной продукции и численности рабочих), и статистическую, или стохастически детерминированную (например, зависимость между производительностью труда и себестоимостью единицы продукции). Функциональная зависимость - связь, при которой каждому значению независимой переменной х: соответствует точно определенное значение зависимой переменной у. Статистическая зависимость - связь, при которой каждому значению независимой переменной х соответствует множество значений зависимой переменной у, причем неизвестно заранее, какое именно значение примет у Частным случаем статистической зависимости является корреляционная зависимость - связь, при которой каждому значению независимой переменной х соответствует определенное математическое ожидание (среднее значение) зависимой переменной у. Корреляционная связь является «неполной» зависимостью, которая проявляется не в каждом отдельном случае, а только в средних величинах при достаточно большом числе случаев. Например: повышение квалификации работника ведет к росту производительности труда. Это положение подтверждается в массе явлений и не означает, что у двух или более рабочих одного разряда, занятых аналогичным процессом, будет одинаковая производительность труда. Уровни выработки будут различаться, так как у этих рабочих могут быть различными стаж работы, техническое состояние станка, состояние здоровья и т.д. Функциональная зависимость всегда выражается формулами, что в большей степени присуще точным наукам (математике, физике) С одинаковой силой проявляется у всех единиц совокупности, является полной и точной, так как обычно известен перечень всех факторов и механизм их воздействия на переменную в виде уравнения. Корреляционная зависимость включает в себя разнообразие факторов. Их взаимосвязи и противоречивые действия вызывают широкое варьирование переменной у. Корреляционная связь обнаруживается не в единичных случаях, а в массе и требует для своего исследования массовых наблюдений Связь между переменными x иу неполная и проявляется лишь в средних величинах Корреляционная связь в зависимости от направления действия бывает прямая и обратная. Ø Прямая корреляционная связь заключается в том, что сувеличением (уменьшением) значений факторного признака происходит увеличение (уменьшение) результативного признака. Ø Обратная корреляционная связь заключается в том, что с увеличением (уменьшением) значений факторного признака происходит уменьшение (увеличение) результативного признака По аналитическому выражению зависимость может быть прямолинейной (линейной) и криволинейной (нелинейной). Ø прямолинейная зависимость: с возрастанием величины факторного признака происходит равномерное возрастание (или убывание) величин результативного признака (выражаются уравнением прямой линии). Ø нелинейная (криволинейная) зависимость: с возрастанием величины факторного признака возрастание (или убывание) результативного признака происходит неравномерно (выражаются уравнениями кривых линий). В зависимости от количества признаков, включенных в модель., корреляционные связи делят на однофакторные и многофакторные. Ø Однофакторные (парные) - связь между одним признаком-фактором и результативным признаком (при абстрагировании влияния других) Ø Многофакторные (множественные) - связь между несколькими факторными признаками и результативным признаком (факторы действуют комплексно, т.е. одновременно и во взаимосвязи). Корреляционная зависимость исследуется с помощью методов корреляционного и регрессионного анализа. Наиболее разработанной в эконометрике является методология парной линейной корреляции, рассматривающая влияние вариации переменной х на переменную у и представляющая собой однофакторный корреляционный и регрессионный анализ. Корреляционный анализ - раздел математической статистики, посвященный изучению взаимосвязей между случайными величинами. Применяется тогда, когда данные наблюдений можно считать случайными и выбранными из генеральной совокупности, распределенной по многомерному нормальному закону Корреляционный анализ заключается в количественном определении тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи). Вопрос 30 Экономико-математическая модель оптимизации мероприятий по освоению и интенсификации использования земель Задача записывается с помощью системы ограничений, которые объединены в пять основных групп: а) ограничения, характеризующие изменения площадей сельхозугодий по плану трансформации. Составляются ограничения по каждому виду угодий. Левая часть ограничения состоит из суммы переменных – площадей различного качества, из которых складывается i – ый вид угодий. Правая часть – сумма существующей площади i – го угодья и переменных, характеризующих увеличение площади за счет трансформации других угодий в i – ый вид. Запись в общем виде: Σ xij ≤ Рi где: xij – площадь i –го угодья, трансформируемого в j-ое, Рi - площадь угодий, пригодная для трансформации Экономико-математическая модель задачи оптимизации трансформации угодий Цель задания: Понять построение оптимизационной экономико-математической модели, характеризующей эффективное использование ресурсов, влияние экономических и технологических условий при установлении размеров производства. Экономические преобразования и связанная с ними интенсификация сельскохозяйственного производства, вызывают необходимость пересмотра состава и соотношения сельскохозяйственных угодий, их перспективного использования. Рациональное использование земельных ресурсов предполагает использование земли по ее прямому назначению, с учетом качественной характеристики почв. Приведение использования земель в соответствии с их качеством, предусматривает мероприятия по трансформации сельхозугодий. В результате трансформации формируется наиболее рациональный состав угодий. При этом происходит перевод из низкопродуктивных угодий в более продуктивные. В результате использования экономико-математических методов удается получать оптимальный состав угодий. Экономико-математическая модель оптимизации состава сельхозугодий решает следующие задачи: - приведение состава сельскохозяйственных угодий в соответствии с их качественной характеристикой; - обеспечение такой структуры сельскохозяйственного угодий, при которой возможно ведение сельскохозяйственного производства в рамках сложившейся специализации и с учетом зональных природных условий; - рациональное использование лимитированных ресурсов (материальных, трудовых и др.) сочетание их с теми видами угодий и того качества, которые обеспечивают наибольший эффект использования сельскохозяйственных угодий. Задача оптимизации структуры сельскохозяйственных угодий формируется следующим образом используя данные о наличие и качестве сельскохозяйственных угодий, урожайности ведущих культур (зерновых) и продуктивности кормовых угодий, норм удельных затрат и объемов ресурсов, определить оптимальную структуру сельхозугодий, при которой за счет рационального использования всех ресурсов, включая земельные, обеспечивается получение максимума чистого дохода при условии обязательного выполнения заказа по договору и зонального удельного веса естественных угодий (пастбищ). Таблица 2
Таблица 3
Построение экономико-математической модели начинают с определением перечня переменных величин, ограничений и выбора целевой функции. Состав переменных модели определяется в соответствии с постановкой задачи и включает следующие группы: - Переменные, которые не имеют альтернативы использования (т.е использования данной площади в данном угодье соответствующей его качеству). - Переменные с возможностью многовариантного использования в различных видах угодий. Запись основных переменных. В рассматриваемой модели в качестве неизвестных x выступают площади i–го угодья j-ого качества. Трансформация проводится с учетом качественной характеристики почв. Система переменных. Х1 - пашня в сад, га Х2–сенокосы в пашню, га Х3–сенокосы в улучшенные сенокосы, га X4– пастбища в пашню, га Х5–пастбища в улучшенные пастбища, га Задача записывается с помощью системы ограничений, которые объединены в пять основных групп: а) ограничения, характеризующие изменения площадей сельхозугодий по плану трансформации. Составляются ограничения по каждому виду угодий. Левая часть ограничения состоит из суммы переменных – площадей различного качества, из которых складывается i– ый вид угодий. Правая часть – сумма существующей площади i –го угодья и переменных, характеризующих увеличение площади за счет трансформации других угодий в i– ый вид. Запись в общем виде: Σxij± Σxijt где: xij – площадь i –xсельхозугодий вида j–ого качества Si- фактическая площадь i – го вида угодья. Ограничения по использованию ресурсов. Размер трансформации всегда определяется наличием ресурсов, от их размеров и соотношения зависит оптимальный состав и соотношения угодий. Тип ограничения будет 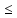 т.к. все ресурсы (если их объем не является искомым) лимитированы. В задачах по оптимизации структуры сельхозугодий выделяются следующие группы ресурсов: т.к. все ресурсы (если их объем не является искомым) лимитированы. В задачах по оптимизации структуры сельхозугодий выделяются следующие группы ресурсов:- по капитальным вложениям. - по минеральным и ограничением удобрениям. - по трудовым ресурсам и др. Запись ограничения по ресурсам в общем виде: 1.Ограничение по капитальным вложениям, руб. 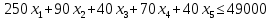 2.Ограничение по средствам механизации, усл. эт. га. 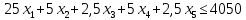 3.Ограничение по трудовым ресурсам, чел.- дн. 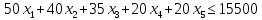 4.Ограничение по удобрениям, ц.д.в. 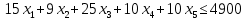 Завершается модель описанием целевой функции, которая отражает чистый доход на участках участвующих и неучаствующих в трансформации и ее величина стремится к максимуму. В общем виде задача записывается следующим образом: Σсijxij –max, где, сij–чистый доход, руб. в расчете на 1 гаi–х сельхозугодий j-гокачества. xij –площадь сельхозугодий i–го вида, j-гокачества. Целевая функция получения максимального чистого дохода при имеющихся ограничениях: 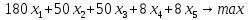 После решения задачи на ЭВМ анализируем полученное решение. Программа Excel предусматривает вывод информации – результаты решения прямой задачи; результаты решения действенной задачи; область значения целевой функции; область значения правой части и др. В распечатке оптимального решения прямой задачи показаны все основные и дополнительные переменные, которые вошли в задачу и значение функции цели. Используя эти данные можно составить ведомость трансформации. Вывод: в результате трансформации получен дополнительный чистый доход в размере 231384 руб. При этом из-за ограничений по некоторым ресурсам в первом случае снижена площадь пастбищ, переводимых в улучшенные пастбища. Во втором случае снижена площадь сенокосов, переводимых в улучшенные сенокосы. Отчёт по результатам до трансформации
1 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
