Вопрос Геодезия
 Скачать 2.8 Mb. Скачать 2.8 Mb.
|
|
k= fэкв/p k – коэффициент дальномера. Обычно так подбирают оптику и сетку нитей, чтобы k=100 D=kl+C; C=f+δ (C – постоянная дальномера) Так подбирают оптические характеристики объектива, чтобы величина С была близка к 0, т.к. для трубы с внутренней фокусировкой для разных расстояний меняется fэкв, следовательно, изменяется k и С, поэтому пользуются формулой D=100l+δ δ – величина переменная, которая берет на себя переменность величин k и С и отличие k от 100. Точность определения расстояний по нитяному дальномеру в среднем 1/300 от расстояния Вопрос 32. Для составления плана местности необходимо знать не расстояние между точками местности, а его горизонтальное проложение. 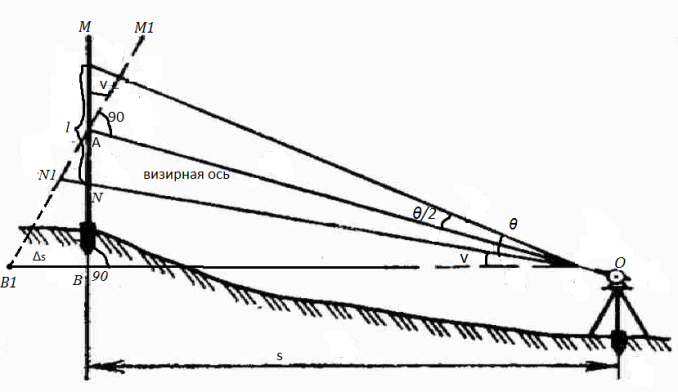 Если бы расстояние MN было известно, то расстояние OB=s=OA*cosν+δ Чтобы получить расстояние ОА надо представить рейку повернутой около точки А и расположенной перпендикулярно визирной оси. По этой воображаемой рейке дальномерный отсчет будет M1N1=l0. Тогда OB=100l0+δ В действительности при работе с вертикальной рейкой получаем дальномерный отсчет l, а не l0, поэтому установим зависимость между действительным отсчетом l и воображаемым l0. Для этого рассмотрим треугольники AMM1и ANN1. Углы в вершине А этих треугольников равны углу наклона ν визирной оси ОА(как углы составленные перпендикулярными сторонами). Углы при точках N1 и M1 в этих треугольниках отличаются от 90 на половину параллактического углаθ (θ≈34,4о). Учитывая, что точность определения расстояния нитяным дальномером невысокая, можно считать треугольники AMM1и ANN1 прямоугольными, вследствие чего l0=lcosν. Подставив имеем OА=100lcosν +δ. Но значение δ в этой формуле очень мало по сравнению с расстоянием 100l, поэтому произведение δcosν не приведет к заметному изменению, а значит OА=(100l +δ)cosν, в итоге S=(100l +δ)cos2ν. Обычно горизонтальное проложение вычисляют через поправку(их может быть несколько). ΔS=(100l +δ)sin2ν. Для углов наклона менее 3о ΔS не значительна и ее можно не учитывать Вопрос 33. Измерение длин линий лентой. Ориентируясь по выставленным вехам, два мерщика откладывают ленту в створе линии, фиксируя концы ленты втыкаемыми в землю шпильками. По мере продвижения измерений задний мерщик вынимает из земли использованные шпильки и использует их для подсчета числа отложенных лент. Измеренное расстояние равно D=20n+r, где n - число отложенных целых лент и r – остаток (отсчет по последней ленте, меньший 20 м). Длину измеряют дважды - в прямом и обратном направлениях. Расхождение не должно превышать 1/2000 (при неблагоприятных условиях - 1/1000). За окончательное значение принимают среднее. Точность измерений лентой в разных условиях различна и зависит от многих причин - неточное укладывание ленты в створ, ее непрямолинейность, изменения температуры ленты, отклонения угла наклона ленты от измеренного эклиметром, неодинаковое натяжение ленты, ошибки фиксирования концов ленты, зависящие от характера грунта и др. Приближённо точность измерений лентой ЛЗ считают равной 1:2000. При благоприятных условиях она в 1,5 – 2 раза выше, а при неблагоприятных – около 1:1000. Вопрос 34. Чтобы найти расстояние между 1-2 выбирают базис, который измеряют на месте, где это удобно делать и измеряют углы β1 и β2. Искомое расстояние D можно определить: D/sinβ1=B1/sin(180-β1-β2); D=B1*sinβ1/sin(β1+β2). Для контроля измерений и вычислений выбирают второй базис и измеряют еще раз 2 угла в треугольнике и аналогичным образом вычисляют D. Допустимым расхождением считается относительная погрешность 1/1000 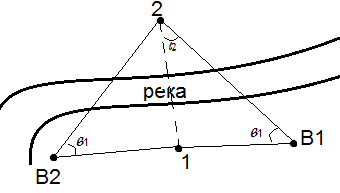 Вопрос 35. Измерение – процесс сравнения измеряемой величины с однородной ей величиной с единицей измерения. Все измерения делятся на прямые и косвенные: а) Прямые – когда результат получается непосредственно при сравнении измеряемой величины с единицей меры(измерение линий и углов). б)косвенные. Измерения делятся на необходимые и добавочные. Путем измерений невозможно получить абсолютно точные значения измеряемой величины, поэтому все измерения сопровождаются погрешностями. Погрешность характеризует точность измерений; это разность между измеренным и точным значением: Δ=l-a (Δ – погрешность; l – результат измерений; a – истинное точное значение). Погрешность получают по правилу: из того, что имеется, вычитают то, что должно быть. Точное значение измеряемой величины можно получить, используя прибор более высокой точности. Например, точная сумма значений измеренных углов в плоском треугольнике 180о, а сумма измеренных углов 179о58,5᾽, тогда погрешность будет составлять -0о01,5᾽. Эту погрешность называют угловой невязкой треугольника. Но одно значение погрешности Δ, вычисленное по формуле, не характеризует точность измерений, потому что, повторяя измерения величины, будем получать различные значения величины l. Поэтому в качестве обобщенной характеристики точности измерений принимают среднюю квадратическую погрешность, вычисляемую по многократным измерениям l1, l2,…ln, а следовательно, и по Δ1,Δ2,…,Δn, пользуясь формулой Гаусса m=  Погрешности Δ и m называют абсолютными и пользуются ими для оценки точности измерений, не зависимых от величины l. Погрешности измерений линий, зависимые от их длины, характеризуют относительными погрешностями, т.е. отношением абсолютной погрешности к результатам измерения: Δ/l– относительная погрешность измерения. Иногда точность измерений характеризуют расхождением между результатами измерений одной и той же величины d=l1- l2 или относительным расхождением d/l. Для определения допустимости расхождений или невязок используют предельные погрешности, которые принимают как удвоенные или утроенные средние квадратические погрешности Δпред = 2m или Δпред = 2m. Вопрос 36. При геодезических измерениях и вычислениях приходится иметь дело преимущественно с приближенными числами. Например, результат измерения линии записан с округлением до двух десятичных знаков или до сотых долей метра – 128,23м. это число неточное, за последней цифрой следует бесконечно большое число цифр, которые отброшены при их округлении, потому что они не соответствуют точности измерения. Для правильного действия с приближенными числами в них различают: десятичные знаки, значащие и верные цифры. Десятичными знаками называют все цифры после запятой, значащими – все цифры числа, кроме нулей справа и слева, если последние при округлении поставлены вместо других цифр. Например, число 4108,207 имеет 3десятичных знака и 7 значащих цифр. Число 0,0035 имеет 4 десятичных знака и 2 значащие цифры. Если говорят, что в населенном пункте 1500 жителей, то в этом числе 2 значащие цифры, т.к. нули поставлены вместо других цифр. Верными называют цифры числа, заслуживающие доверия. Например, если результат измерения записан так: 128,23м, а измерение проводили с точностью до 1м, то в этом числе будут лишь 3 верные цифры, а последние не заслуживают доверия.В таком числе, как 180, выражающем сумму углов плоского треугольника, число верных значащих цифр бесконечно большое. При вычислениях выдерживают такое число значащих цифр, десятичных знаков, которое обеспечивает нужную точность результатов и не загружает вычисления неверными или ненужными цифрами.
Сложение и вычитание приближенных чисел. Если числа содержат неодинаковое число десятичных знаков, то при их сложении и вычитании оставляют столько десятичных знаков, сколько их имеет приближенное число с наименьшим числом десятичных знаков плюс одна запасная цифра. Например, при сложении чисел, имеющих верные значащие цифры: 12,13754+0,27+287,6+1253,852 число 287,6 имеет наименьшее число десятичных знаков, остальные число надо округлить: 12,14+0,27+287,6+1253,85=1553,9. Полученный результат содержит все верные значащие цифры. Сумма или разность приближенных чисел имеет столько верных десятичных знаков, сколько их имеет число с наименьшим количеством десятичных знаков. Поэтому в слагаемых в сумме должно быть одинаковое число десятичных знаков.
Умножение и деление приближенных чисел. Если числа содержат неодинаковое число значащих цифр, то при умножении и делении их оставляют столько значащих цифр, сколько их содержит приближенное число с наименьшим количеством значащих цифр, плюс одна запасная значащая цифра. Например при умножении и делении чисел 12827,53 2,13, у которых все значащие цифры верные, число с наименьшим количеством значащих цифр будет 2,13. Поэтому перед умножением или делением другое число надо округлить до 12830. если этого не сделать, то число будет иметь большое количество неверных цифр. 12830*2,13=27300=2,73*104, т.е. в полученном числе 3 верные значащие цифры. Произведение и частное имеют столько верных значащих цифр, сколько их в числе с наименьшим количеством значащих цифр. В связи с этим в сомножителях и произведении должно быть одинаковое число значащих цифр. Возведение в степень и извлечение корня. По аналогии с произведением при возведении числа в степень в полученном числе надо оставить столько значащих цифр, сколько их было в числе, возводимом в степень, т.е. 42,272=1787. Если в результате извлечения корня требуется получить 4значащие цифры, то в подкоренном числе надо оставить такое же число значащих цифр, т.е. брать не 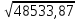 =220,3, а =220,3, а 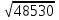 =220,3. =220,3.Вопрос 38. Вопрос 39. Вопрос 40. Вопрос 42. Съемка ситуации – геодезические измерения на местности для последующего нанесения на план ситуации (контуров и предметов местности). Выбор способа съемки зависит от характера и вида снимаемого объекта, рельефа местности и масштаба, в котором должен быть составлен план . Съемку ситуации производят следующими способами: перпендикуляров; полярным; угловых засечек; линейных засечек; створов (рис. 60). Способы съемки ситуации: 1) способ перпендикуляров; 2) полярный способ; 3) способ угловых засечек; 4) способ линейных засечек; 5) способ створов. 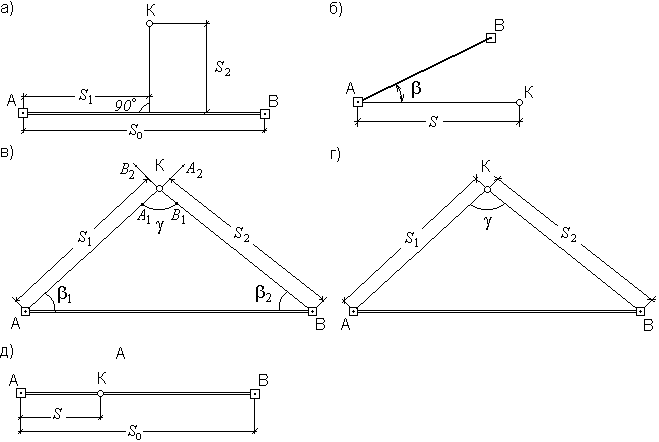 Рис. 60. Способы съемки ситуации: а – перпендикуляров, б – полярный, в – угловых засечек, г – линейных засечек, д – створов. Способ перпендикуляров (способ прямоугольных координат) – применяется обычно при съемке вытянутых в длину контуров, расположенных вдоль и вблизи линий теодолитного хода, проложенных по границе снимаемого участка. Из характерной точки К (рис. 60, а) опускают на линию хода А – В перпендикуляр, длину которого S2измеряют рулеткой. Расстояние S1 от начала линии хода до основания перпендикуляра отсчитывают по ленте. Полярный способ (способ полярных координат) – состоит в том, что одну из станций теодолитного хода (рис.60, б) принимают за полюс, например, станцию А, а положение точки К определяют расстоянием S от полюса до данной точки и полярным углом β между направлением на точку и линией А – В. Полярный угол измеряют теодолитом, а расстояние дальномером. Для упрощения получения углов, теодолит ориентируют по стороне хода. При способе засечек (биполярных координат) положение точек местности определяют относительно пунктов съемочного обоснования путем измерения углов β1 и β2(рис.60, в) – угловая засечка, или расстояний S1 и S2 (рис.60, г) – линейная засечка. Угловую засечку применяют для съемки удаленных или труднодоступных объектов. Линейную засечку – для съемки объектов, расположенных вблизи пунктов съемочного обоснования. При этом необходимо чтобы угол γ, который получают между направлениями при засечке был не менее 30° и не более 150°. Способ створов (промеров). Этим способом определяют плановое положение точек лентой или рулеткой.(рис. 60, д). Способ створов применяется при съемке точек, расположенных в створе опорных линий, либо в створе линий, опирающихся на стороны теодолитного хода. Способ применяется при видимости крайних точек линии. Результат съемки контуров заносят в абрис. Абрис называют схематический чертеж, который составляется четко и аккуратно. |
