Вопрос Геодезия

• Название: Вопрос Геодезия
• Анкор: Ekzamen (1).docx
• Дата: 15.09.2018
• Размер: 2.8 Mb.
• Имя файла: Ekzamen (1).docx
• Тип: Документы; #24633
• страница: 4 из 5

Вопрос 43.

Способы определения площадей земельных участков:

Выделяют 3 способа определения площадей земельных участков:

-аналитический (площадь определяется по результатам измерений – мер линий и углов – на местности или их функциям – координатам, приращениям)

-графический (площадь определяется по результатам измерений – мер линий и углов или координат точек контура – на планово-картографическом материале)

-механический (площадь участка определяется при помощи планиметра непосредственно по плану,карте)

Аналитический способ:

Когда координаты поворотных точек неизвестны или нецелесообразно прокладывать теодолитный ход, участок делят на простейшие геометрические фигуры: -треугольник (по стандартной формуле площади)

- четырехугольник (через измеренные 3 стороны и углы, заключенные между ними)

2Р=a*c*sin (

-трапеция(по 2 измеренным основаниям и углам при основании)

2Р=-)/(ctg

Графический способ:

Площадь определяют по результатам измерений на плане, при этом участки разбивают на простейшие геометрические фигуры, преимущественно треугольники, реже на прямоугольники и трапеции. В каждой фигуре на плане измеряют высоту и основание, по которым вычисляют площадь. При вычислении площадей фигур пользуются такими же формулами, как и при аналитическом способе. Сумма площадей фигур дает площадь участка.

Наилучшим вариантом разбивки участка на треугольники будет тот, при котором треугольники близки к равносторонним (точнее, высоты по величине близки к основаниям).

Механический способ:

Стоит применять этот способ в тех случаях, когда границы участка сильно изломаны. Работу выполняют планиметром. При использовании планиметра площадь фигуры определяется по формуле Р=u*p, где u-количество делений, р-цена деления.

Для обеспечения контроля измерения выполняют по 2 раза при положении полюса справа и слева.

Вопрос 44.



Вопрос 45.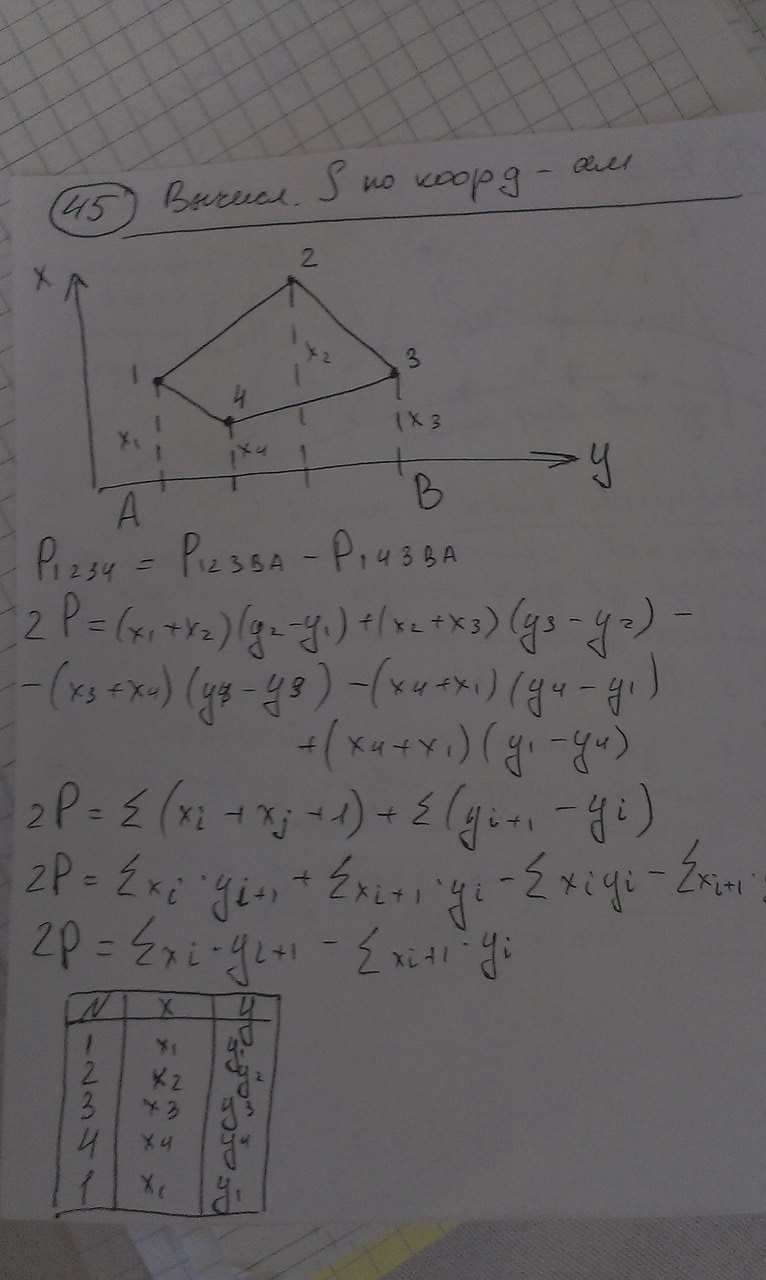



Вопрос 46.

При графическом способе площадь определяют по результатам измерений на плане (карте), при этом участки разбивают на простейшие геометрические фигуры, преимущественно треугольники, реже на прямоугольники и трапеции. В каждой фигуре на плане измеряют высоту и основание, по которым вычисляют площадь. При вычислении площадей фигур пользуются такими же формулами, как и при аналитическом способе. Сумма площадей фигур дает площадь участка. Число треугольников не влияет на точность определения площади. Для повышения точности и исключении влияния систематических погрешностей в смежных фигурах общие стороны измеряются независимо (результаты, полученные в предыдущей фигуре, не используют в следующей), для контроля используют другие высоты и основания.

Наилучшим вариантом разбивки участка на треугольники будет тот, при котором треугольники близки к равносторонним (вернее, высоты по величине близки к основаниям). К рассматриваемому способу относится и применяемый в настоящее время прием определения площади участка по координатам поворотных точек границ, снятым графически с плана или определенным фотограмметрическим способом. В последние годы разработаны специальные устройства широкого назначения (цифрователь – дигитайзер, координатометр, сканер), позволяющие преобразовывать графическое изображение контуров ситуации на планах (картах) в цифровое в виде координат точек. Считанная такими устройствами и переданная в компьютер информация может быть затем использована для вычисления площади участка, определения протяженности границ и других целей в зависимости от имеющихся программ обработки.

У цифрователей (дигитайзеров) отсутствуют механические счетные устройства, что обеспечивает высокую точность измерения независимо от качества поверхности планов (карт). Кроме того, исключаются производство отсчетов при измерениях, вычислительная обработка и подготовка результатов измерений к обработке на компьютере. Тем самым значительно повышается производительность труда, а увеличение количества точек контура с измеренными графическими координатами повышает точность определения площади, приближая её к аналитическому способу.

Суммарная погрешность определения площади участка по плану (карте) графическим способом зависит:

1) от погрешностей полевых измерений, сопутствующих составлению плана;

2) от погрешности изображения площади участка на плане;

3) от погрешности непосредственных измерений на плане.

Примечание. Средняя квадратическая погрешность определения координат измерителем по масштабной линейке равна 0,18 мм; при помощи координатографа или фотограмметрическим способом координаты можно определять с погрешностью 0,05 мм и менее; погрешность измерения расстояния измерителем по масштабной линейке 0,1 мм.

При этом в суммарной погрешности основную долю составляет влияние погрешности изображения границ участка на плане. Если эта погрешность не удовлетворяет требованиям землеустройства и кадастра недвижимости, то для повышения точности расчета необходимо использовать план более крупного масштаба. Тогда доля основной погрешности соответственно масштабу плана уменьшается.

Вопрос 47.

Для определения на плане площадей небольших участков с криволинейными контурами применяют квадратные и параллельные палетки, выполненные на прозрачной основе (Рис 4, а).

При использовании квадратных палеток площадь фигуры вычисляют простым подсчетом клеток палетки, наложенной на фигуру. Площадь вычисляют по формуле:

Р= n*U,
где n- число клеток палетки,

U- цена деления палетки в га.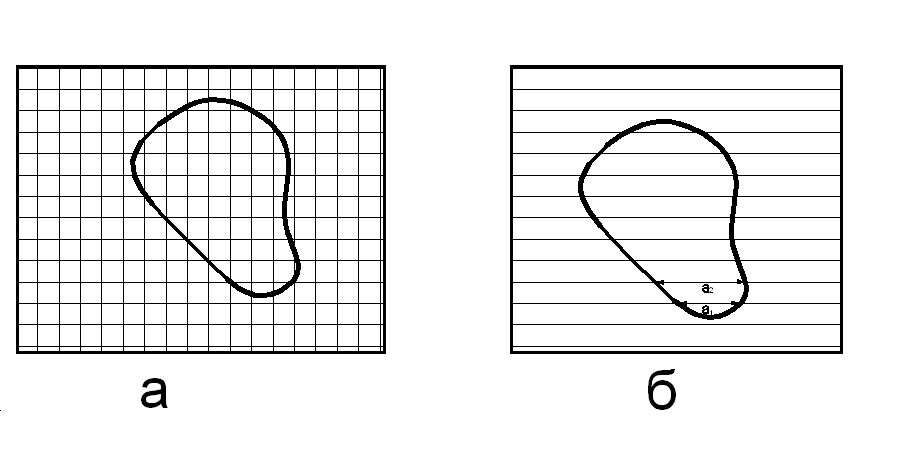

Рис 4 а) квадратная палетка, б) параллельная палетка
При использовании параллельной палетки измеряют отрезки, которые являются средними линиями трапеций, высотами трапеций является отрезок между параллельными линиями (Рис 4 б). Площадь вычисляют по формуле:

Р= h*а ,

Где h- расстояние между параллельными линиями в масштабе плана,

а- сумма длин параллельных отрезков заключенных в пределах

Вопрос 48.

Механический способ определения площадей предполагает измерение площади участка непосредственно на плане планиметром. Этот способ целесообразно применять в тех случаях, когда границы участка сильно изломаны. Перед началом работы планиметр испытывают, поверяют и выполняют юстировку.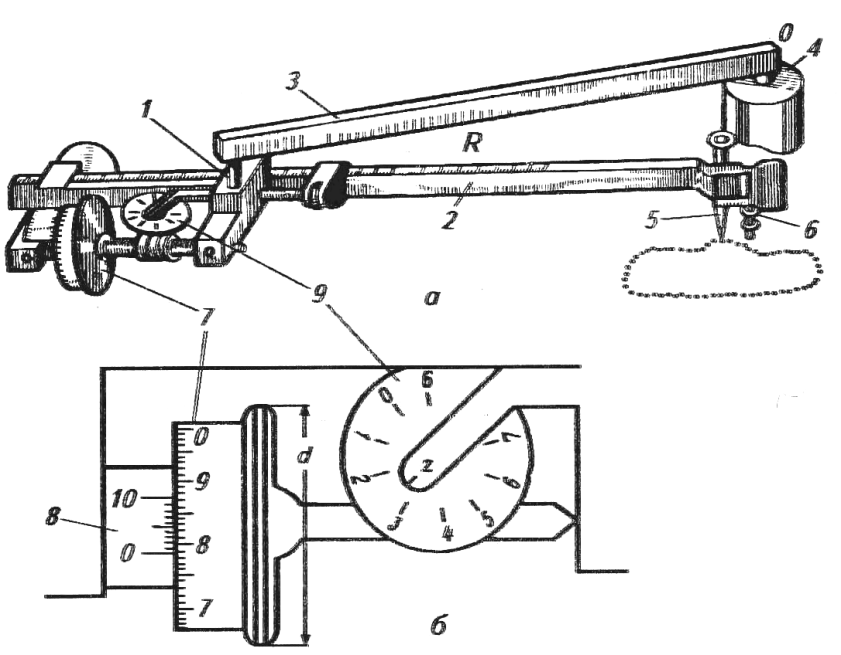




Рис. 5. Схема планиметра.

1– шарнирное соединение рычагов;

2 – обводной рычаг;

3 – полюсный рычаг;

4 – полюс;

5 – обводной индекс;

6 – опорный винт (штифт);

7 – счетный ролик;

8 – верньер (нониус);

9 – циферблат счетного механизма;

10 - θ – угол между полюсным и обводным рычагами;

11 - 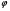- угол из-за невыполнения основного геометрического условия.
Требования к планиметру:

1) Счетный ролик должен свободно вращаться не менее 3 секунд.

2) Показания счетного ролика должны быть устойчивыми при следующих значениях угла θ:

1 позиция - ;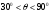

2 позиция - ;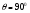

3 позиция - ;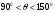

При использовании планиметра площадь фигуры определяется по формуле:

P=u*ρ,

где u- количество делений,

ρ - цена деления.

Цена деления планиметра это площадь прямоугольника с основанием равным длине обводного рычага и высотой равной одному делению планиметра.

Цену деления планиметра определяют, измеряя известную площадь, например, площадь квадрата координатной сетки.

ρ= Р_кв /u _кв ,

где Р_кв – площадь квадрата в га,

u_кв - количество делений планиметра при обводе квадрата.
Для обеспечения контроля измерения площадей обвод фигур для определения площадей и цены деления выполняют по 2 раза при положении полюса с права и с лева.

Площади землепользований коллективных и других хозяйств вычисляют обычно аналитическим способом, если по границам их проложены теодолитные ходы. Границы угодий входящих в состав землепользования определяют различными способами аналитическим, графическим, механическим.

Уравнивание площадей при таких условиях заключается в сравнении значений площади землепользования определенной аналитически (как более точного определения  Р_теор) и суммы площадей угодий входящих в землепользование  P_пр.

Невязку в сумме площадей контуров вычисляют по формуле:

f_p =  P_пр –  Р_теор

Допустимость невязки определить по формуле:
f_p^доп = 0.7 · р ·  n + 0.05 · (М/10000) ·  Р
где р ― цена деления планиметром;

n ― число контуров, площади которых определяют планиметром;

М ― знаменатель численного масштаба плана;

Р ― общая площадь опытного участка.

Невязку, если она допустима, распределить на площади контуров пропорционально коэффициентам поправок, выбираемым из специальных таблицы .

По результатам вычисленных площадей угодий составляют экспликацию земель.

Вопрос 49.

Цена деления бывает абсолютной ( µ абс),' если она

выражена в мм2 /дел., и относительной ( µ отн), если выражена в м2 /дел. или га/дел., с учетом

масштаба данного плана (карты).

Для определения цены деления планиметра выбирают фигуру, площадь которой Sо известна

заранее (например, один или несколько квадратов координатной сетки). С целью получения более

высокой точности выбранную фигуру обводят по.. контуру четыре раза: два раза при положении

«полюс право» (ПП) и два — при положении «полюс лево» (ПЛ). При каждом обводе берут на-

чальный и конечный отсчеты и вычисляют их разность (ni - noi). Расхождения между значениями

разностей, полученными при ПП и ПЛ, не должны превышать при площади фигуры до 200 деле-

ний—2, от 200 до 2000 делений—3 и свыше 2000—4 деления планиметра. Если расхождения не

превышают допустимых, то рассчитывают среднюю разность отсчетов (п - nо)ср и вычисляют цену деления планиметра по формуле

µ= (n − n 0 ) ср

Вопрос 50.

Вопрос 51.

При разбивке участка на простейшие фигуры точность вычисления для различных вариантов не будет одинаковой. Площадь треугольника графическим способом вычисляется точнее, чем площади других фигур. Следовательно, площадь при разбивке участка на треугольники вычисляется точнее, чем при разбивке на другие фигуры (трапеции, прямоугольники). При разбивке участка на треугольники из всех вариантов будет лучшим тот, в котором треугольники будут равносторонними или высота h примерно равна основанию a.

Погрешность уменьшается, если вычислять площадь треугольника не как , а по формуле Герона

,

где . Это дает уточнение до 13% даже для равностороннего треугольника. Основание треугольника может быть во много раз меньше высоты, если оно измеряется на местности, а не на плане.

При разбивке площади на треугольники погрешность площади участка

,

где M – знаменатель численного масштаба плана. Если 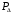вычисляют два раза, то .

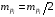Число треугольников, на которое разбивается участок, не влияет на погрешность площади. Поэтому при разбивке участка на треугольники не надо стремиться к тому, чтобы их было меньше. Точность однократного определения площади квадратной и параллельной палетками, а также ротометром характеризуется эмпирической формулой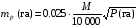

.

Вопрос 52.

Вопрос 53.

Нивелирование– определение превышений между точками земной поверхности.
Нивелирование выполняют различными приборами и разными способами, различают:

-геометрическое (при помощи прибора нивелира, которое обеспечивает горизонтальное положение визирной оси - самое точное: превышение между точками – разность отсчетов по рейке)

-тригонометрическое (превышение между точками определяют по измеренному вертикальному углу и расстоянию между точками, т.е. нивелирование наклонной визирной оси теодолита или тахеометра)

-барометрическое (основано на использовании зависимости между атмосферным давлением и высотой точки на местности)

-гидростатическое (основано на свойствах жидкости сообщающихся сосудов, находиться на одном уровне)

-радиолокационное (при аэрофотосъемке, основано на измерении времени прохождения радиолуча).

Вопрос 54.

Геометрическое нивелирование

Выполняется при помощи горизонтального визирного луча. Точность определения превышение может достигать десятых долей миллиметра. Имеет наиболее широкое применение, поскольку самый точный способ. Выполняется двумя способами: «вперед» и «из середины»
Нивелирование «вперед»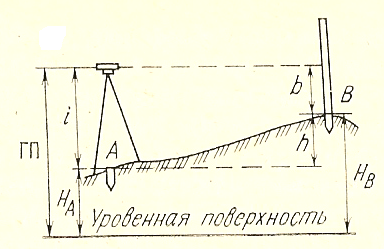

Для определения превышения между точками А и В на точку с известной отметкой (заднюю) устанавливают нивелир таким образом чтобы его окуляр находился на одной отвесной линии с этой точкой и при помощи рулетки измеряют высоту инструмента i. В точку отметку которой определяют (переднюю) вертикально устанавливают рейку и берут по ней отсчет b.

Отсчет по рейке – расстояние от начала рейки до проекции на нее визирной оси.

h=i–b

H_b=H_a+h

Отметку точки В можно вычислить через горизонт инструмента (ГИ).

Горизонт инструмента – расстояние от средней уровенной поверхности до визирного луча прибора.

ГИ=H_a+i

H_b=ГИ–b
Нивелирование «из середины»

Для определения превышения между точками А и В на них вертикально устанавливают рейки и на равном удалении от них устанавливают нивелир, приводят его в рабочее положение.

Визируют на заднюю и переднюю точки и берут отсчеты по рейкам (а и b).

Превышение равно разности отсчетов на заднюю и переднюю точки

h=a–b

ГИ=H_a+a

H_b=H_a+h=ГИ–b

Вопрос 55.

Горизонт прибора – расстояние от средней уровенной поверхности до визирного луча прибора.



Вопрос 57.

Нивелир – прибор, обеспечивающий горизонтальное положение визирной оси.

Общий вид нивелира



Рис. 5


1 – зрительная труба;

2 – цилиндрический уровень при трубе;
3 – элевационный винт;

4 – круглый уровень (на рисунке не показан);
5,6 – закрепительный и наводящие винты;
7 – вертикальная ось нивелира (ZZ₁);
8 – подставка с тремя подъемными винтами.
Вопрос 58.

Ось круглого уровня должна быть параллельна оси вращения нивелира ZZ || ii.

Подъёмными винтами приводят пузырёк круглого уровня в центр кружка на ампуле уровня и поворачивают верхнюю часть прибора на 180°. При отклонении пузырька от центра ампулы перемещают его к центру на половину отклонения с помощью исправительных винтов круглого уровня. Окончательно приводят пузырек уровня на середину подъемными винтами. Если уровень исправился, то поверку необходимо повторить.
2. Горизонтальная нить сетки должна быть перпендикулярна оси вращения нивелира.

С помощью круглого уровня приводят ось вращения нивелира в отвесное положение. Среднюю нить наводят на ясно видимую точку и наводящим винтом плавно вращают трубу в горизонтальном направлении. Нить сетки не должна сходить с выбранной точки. Эту же поверку можно делать, наводя вертикальную нить сетки на нить отвеса. При несоблюдении условия необходимо снять защитный колпачок и развернуть сетку нитей, предварительно ослабив четыре винта в торце окулярной части трубы отверткой.
3. Ось цилиндрического уровня должна быть параллельна визирной оси трубы («главное условие нивелира») VV || UU.

Первая часть главного условия проверяется двойным нивелированием вперед. На местности забивают два колышка на расстоянии около 50 м один от другого. Нивелир устанавливают над точкой А так, чтобы окуляр трубы находился на одной вертикальной линии с точкой (рис.4). От колышка до центра окуляра измеряют высоту прибора i₁. Затем рейку ставят в точку В, наводят на нее трубу нивелира, приводят пузырек уровня в нуль-пункт и берут отсчет по рейке b₁. Затем нивелир и рейку меняют местами, измеряют высоту прибора i₂, приводят пузырек уровня в нуль-пункт и берут отсчет по рейке b₂ (рис.7).



Рис. 7
Пусть главное условие нивелира не выполняется, и при положении пузырька уровня в нуль-пункте визирная линия не горизонтальна, а составляет с осью уровня некоторый угол i. Тогда вместо правильного отсчета b⁰ ₁ получается ошибочный - b₁. Ошибку отсчета обозначим x, и превышение точки В относительно точки А будет равно:

h = i₁ - (b₁ + x).

При положении нивелира в точке В превышение точки А относительно точки В:

h' = i₂ - (b₂ + x).

Но h = - h', поэтому

i₁ - (b₁ + x) = - [i₂ - (b₂ + x)].

Отсюда получаем:

x = 0.5*(i₁ + i₂) - 0.5*(b₁ + b₂).     

Если x получается больше 4 мм по модулю, необходимо выполнить юстировку уровня, т.е. устранить угол i. Для этого элевационным винтом наклоняют трубу нивелира до тех пор, пока отсчет по рейке не будет равен правильному отсчету: b⁰₂ = b₂ + x, при этом пузырек уровня уйдет из нуль-пункта. Исправительными винтами уровня приводят пузырек в нуль-пункт и повторяют поверку заново.

При нивелировании строго из середины ошибка отсчета по рейке из-за невыполнения главного условия нивелира не влияет на величину измеряемого превышения (рис.8).



Рис. 8