Вопрос Инверсия населенности уровней
 Скачать 176.5 Kb. Скачать 176.5 Kb.
|
|
Вопрос 1. Инверсия населенности уровней. Считая спонтанное излучение достаточно малым, рассмотрим условия, при которых в системе частиц, при воздействии внешнего электромагнитного поля возможно индуцированное излучение. Пусть система характеризуется двумя энергетическими состояниями Е1 и Е2 (E2 < E1) и числом частиц на этих уровнях N1 и N2 соответственно. Частота колебаний внешнего излучения равна а плотность энергии uυ. Частицы в системе, находящейся в нормальном состоянии термодинамического равновесия, распределяются по энергетическим уровням в соответствии с функцией распределения статистики Больцмана. Более высокий энергетический уровень заселен меньшим числом частиц (N2 < N1). При повышении температуры функция F(Е) становится более пологой, но условие N2 < N1 выполняется при любой конечной температуре. Вероятности индуцированных переходов в системе вверх и вниз определяются соотношениями (7-14) и (7-15). При условии, что B21 = B12 = B и N2 < N1, P'21 < Р'12. В системе преобладают индуцированные переходы вверх. Система частиц поглощает энергию внешнего электромагнитного поля. С подобными явлениями мы часто сталкиваемся в жизни: радиоволны затухают при распространении в атмосфере земли, интенсивность световых волн падает при их прохождении через различные среды и т. д. В рассматриваемой системе частиц будет преобладать индуцированное излучение лишь в том случае, если вероятность переходов вниз будет больше вероятности переходов вверх (P'21 > Р'12). Это возможно лишь при условии, что на верхнем энергетическом уровне будет больше частиц, чем на нижнем: N2 > N1. Состояние вещества или системы, в которой выполняется это условие, что населенность верхнего энергетического уровня будет больше, чем нижнего: N2 > N1 называется состоянием с инверсией (обращением) населенности уровней. Или, просто говорят, что в системе наблюдается инверсная населенность уровней. Вещество с инверсной населенностью называют активным веществом. Вопрос 2. Распределение Больцмана. Иногда инверсную населенность характеризуют отрицательной температурой. Этот термин можно объяснить следующим образом. В соответствии с законом распределения статистики Больцмана для отношения числа частиц на двух уровнях (7-8) и (7-9) можно записать: 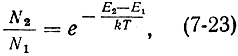 отсюда 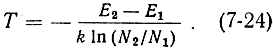 Если N2 < N1, то T > 0. При любой конечной положительной температуре на нижнем энергетическом уровне находится большее число частиц. Частицы в системе стремятся занять состояния с меньшей энергией. С повышением температуры экспонента на рис. 7.1 становится более пологой, но в любом случае выполняется неравенство N2 < N1. 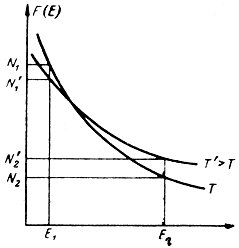 Рис. 7.1. Кривые распределения Больцмана частиц по энергетическим состояниям Температура становится отрицательной только при условии N2 > N1, что соответствует инверсной населенности уровней. Чем сильней неравенство N2 > N1, тем более "отрицательна" температура. Следует иметь в виду, что температура Т, о которой идет речь, не является абсолютной температурой вещества, ибо отрицательная абсолютная температура с физической точки зрения не имеет смысла. Температура Т в (7-24) - это некоторая условная величина - температура квантового перехода, используемая в квантовой электронике для характеристики отношения населенностей уровней. При равенстве населенностей уровней (N1 = N2) температура Т = ∞. Система находится в состоянии насыщения; она прозрачна для внешнего излучения, так как число переходов вниз в среднем равно числу переходов вверх. Вполне понятно, что из этих трех возможных состояний (Т < 0; T > 0 и Т = ∞) устойчивым является лишь одно, отвечающее положительной температуре. В одно из двух других - возбужденных - состояний система может быть переведена при затрате некоторой внешней энергии и лишь при определенных условиях. В квантовых приборах в качестве активных подбираются такие вещества, в которых индуцированные переходы вниз сопровождались бы излучением электромагнитной энергии с требуемой частотой. Задача получения и поддержания в течение нужного времени активного состояния вещества, т. е. состояния с инверсной населенностью - одна из важнейших задач квантовой электроники. Вопрос 3. Что такое активная среда? Это среда населенности уровней не подчиняются законам статистики Больцмана. Вопрос 4. Закон Бугера. Интенсивность электромагнитной волны нарастает с координатой z по экспоненциальному закону (закон Бугера) uν(z) = u0ν eχz. (7-39) 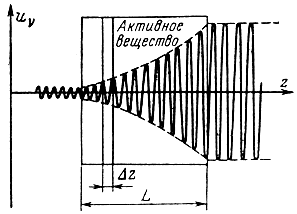 Рис. 7.6. Квантовое усиление колебаний В соответствии с (7-39) интенсивность электромагнитной энергии на пути z = 1/χ возрастает в е раз, а по выходе из вещества достигнет величины u0ν eχL. Величина χ, имеющая размерность [см-1], называется коэффициентом квантового усиления. Его величина пропорциональна вероятности Р'21 индуцированных переходов 2 → 1, числу активных частиц и величине кванта hν12 χ ∼ P'21 ΔNν12. (7-40) Вопрос 5. Чем определяется возможность усиления электромагнитных волн веществом? Величина χ, имеющая размерность [см-1], называется коэффициентом квантового усиления. Его величина пропорциональна вероятности Р'21 индуцированных переходов 2 → 1, числу активных частиц и величине кванта hν12 χ ∼ P'21 ΔNν12. (7-40) Вопрос 6. Условия квантового усиления и генерации (условие самовозбуждения). Условие квантового усиления. Рассматриваемая система, как и любая другая, не свободна от потерь. Часть электромагнитной энергии через выходную линию отводится в нагрузку; определенная доля энергии теряется в самом резонаторе и в активном веществе. Поэтому режим работы системы зависит от соотношения между энергией Eизл, поступающей в резонатор за счет индуцированного излучения, и суммарной энергией потерь Еп. Если Eизл + Eс:вх < Eп, то подводимая ко входу энергия сигнала Eс.вх поглощается системой, амплитуда колебаний на выходе меньше амплитуды колебаний на входе: Eс.вых < Eс.вх. Если энергия Eизл + Eс.вх (энергия Eизл, поступающая в резонатор за счет индуцированного излучения и подводимая ко входу энергия сигнала Eс.вх ) превышает потери в резонаторе и активном веществе, но меньше суммарной энергии Еп потерь, включающей отвод энергии в нагрузку, Eр < Eизл + Eс:вх < Eп то система работает как усилитель. Амплитуда колебаний в выходной линии больше амплитуды колебаний, подводимых ко входу: Eс.вых > Eс.вх. Таким образом, система представляет собой усилитель с положительной обратной связью, обеспечиваемой резонатором, в который помещено активное вещество. Необходимые фазовые условия выполняются за счет преимущественного заселения верхнего энергетического уровня рабочего перехода. Увеличение энергии сигнала обусловлено преобладающим индуцированным излучением - размножением квантов энергии в активном веществе, когерентных входному сигналу. Энергетические соотношения в системе таковы, что энергия индуцированного излучения, обеспечивая режим квантового усиления, недостаточна, однако, для поддержания режима самовозбуждения. Условие квантовой генерации (режим самовозбуждения). Если Eизл > Eп , то система перейдет в режим самовозбуждения и превратится в генератор. Энергия Eизл, получаемая за счет индуцированного излучения, должна быть достаточной для восполнения как потерь в резонаторе самого генератора, так и части энергии, отводимой в нагрузку Eр В этом случае колебания в системе будут существовать даже при отсутствии сигнала на входе. Для поддержания колебаний стационарной амплитуды должны быть выполнены определенные условия, необходимые для сохранения неравенства Eизл > Еп. Иначе говоря, в рассматриваемой системе, как и в любом автогенераторе, должен выполняться баланс мощностей. Величина энергии Eизл пропорциональна числу ΔN активных частиц. По мере осуществления индуцированных переходов 3 → 2 верхний энергетический уровень E3 рабочего перехода опустошается, а уровень Е2 заселяется частицами. Для поддержания нужной величины ΔN плотность энергии накачки должна быть достаточной для обеспечения необходимой скорости заселения уровня Е3 частицами с уровня Е1. Кроме того, необходима определенная скорость опустошения уровня Е2 за счет релаксационных переходов 2 → 1. Все эти процессы в режиме стационарной амплитуды колебаний должны находиться в динамическом равновесии. Вопрос 7. Пояснить физические основы работы лазера.  Вопрос 8. Дать функциональную схему оптического квантового генератора (лазера). 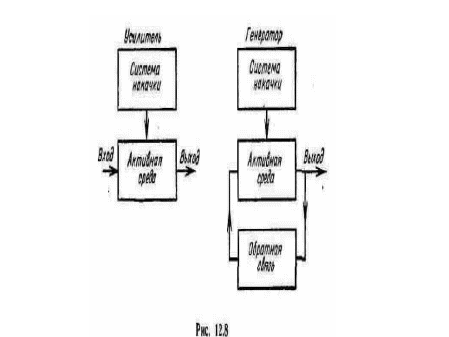 Вопрос 9. Указать методы создания инверсной населенности в квантовых генераторах оптического диапазона. Для создания инверсной населённости среды лазера используются различные механизмы. В твердотельных лазерах она осуществляется за счёт облучения мощными газоразрядными лампами-вспышками, сфокусированным солнечным излучением (так называемая оптическая накачка) и излучением других лазеров (в частности, полупроводниковых). Вопрос 10. Пояснить физические основы работы мазера.  Вопрос 11. Дать функциональную схему квантового парамагнитного усилителя СВЧ (мазера).  Вопрос 12. Указать методы создания инверсной населенности в квантовых парамагнитных усилителях СВЧ (мазерах). Накачка вспомогательным излучением (накачка СВЧ полем), метод сортировки частиц. |
