Вопрос Основные физические характеристики звука и соответствующие им сенсорные качества
 Скачать 1.75 Mb. Скачать 1.75 Mb.
|
|
Вопрос 1. Основные физические характеристики звука и соответствующие им сенсорные качества. Основными физическими характеристиками звуковых волн являются частота, амплитуда, или интенсивность, и сложность. Ниже мы рассмотрим каждую из этих характеристик отдельно и одновременно расскажем об их психологических эффек тах (о высоте, громкости и тембре соответственно).  Частота Одной из характеристик звуковых волн, свидетельствующей о том, насколько бы стро протекает цикл изменений давления, является число циклов изменения давле ния (т. е. переходов от сжатия к разрежению и обратно), происходящих в течение 1 с. Она называется частотой (f) и измеряется в герцах (Гц); единица измерения часто ты, названная в честь немецкого физика Генриха Герца (1857-1894), равна числу изменений звукового давления, или циклов, в секунду. Так, если частота звука равна 1000 Гц, значит за секунду происходит 1000 циклов, или изменений, звукового дав ления (рис. 12.2). Считается, что молодые люди способны воспринимать звуки с частотой от 20 до 20000 Гц; звуки, частота которых ниже 20 или выше 20000 Гц, находятся ниже и выше порога слухового восприятия человека.  Частота и длина волны. Для описания звуковых волн используется также и такая характеристика, как длина одиночной волны. Как будет ясно из материала, изложенного в главе 14, это свойство весьма полезно для понимания многих аспек тов такого феномена, как локализация звука. Длина звуковой волны — это линей ное расстояние между двумя последовательными компрессиями (этот параметр обозначается греческой буквой — λ) (рис. 12.3). Длина волны обратно пропорциональна частоте (т. е.λ=v/f ). Так, в воздушной среде длины волн звуков, распространяющихся с постоянной скоростью 335 м/с и имеющих частоту 1100, 550 и 2200 Гц, равны 30,48; 60,96 и 15,24 см соответствен но. Чем больше частота звука, тем чаще в течение определенного промежутка вре мени изменяется давление, тем ближе пики и подошвы звуковой волны примыка ют друг к другу и тем короче сама волна. Так, низкочастотный звук имеет длинную волну, а высокочастотный — короткую (рис. 12.4). Из графика следует, что длина волны звука с частотой 1100 Гц равна 30,48 см. 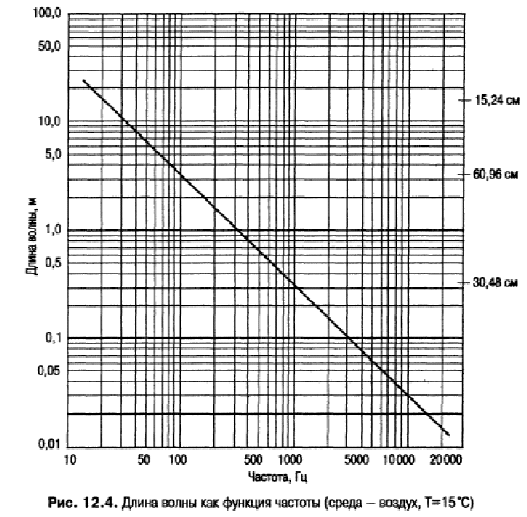 Высота звука. Частота характеризует физическое свойство звука — число из менений звукового давления в секунду. Психологическим параметром аудиального стимула, непосредственно связанным с его частотой, является абсолютная вы сота тона, и звуки разной высоты вызывают у слушателей разные ощущения: они могут казаться высокими или низкими. Высота звука изменяется в очень широких пределах, и известны как очень низкие, басовые, звуки, так и исключительно высокие, дискантовые. Амплитуда Звуки отличаются друг от друга не только по высоте, но и по амплитуде — коли честву изменения звукового давления, т. е. степени смещения (компрессии или декомпрессии) относительно положения покоя (рис. 12.2). При низком давлении амплитуда звука мала и звук слабый, при высоком давлении воздуха амплитуда звука велика и слышен интенсивный звук. (Характеризующие звук термины амп литуда и интенсивность — взаимозаменяемые.) Будучи физическим параметром, амплитуда, или интенсивность, звука зависит от давления или силы, воздействующих на его источник. Основной единицей изме рения давления является сила на единицу площади. Несмотря на то что давление звука может быть выражено во многих других единицах, для удобства в акустике (разделе физики, занимающемся изучением упругих волн) давление измеряется в динах на квадратный сантиметр (дин/см2). Иногда давление звука оценивается в эквивалентной единице — в микробарах, сокращенно мбар. Сравнительно недав но изменение давления стали выражать в ньютонах на квадратный метр, Н/м2, и микропаскалях, мкПа. Децибел (дБ). Интервал амплитуд, к которым чувствительно ухо, чрезвычай но широк. Сила самого громкого звука в миллиарды раз превышает интенсивность самого слабого звука, улавливаемого человеческим ухом. Поскольку этот интер вал огромен, удобно пользоваться логарифмической шкалой давлений, названной в честь Александра Грэма Белла децибельной (дБ) шкалой. Преимущество лога рифмической шкалы децибелов для оценки интенсивности звука заключается В том, что она сокращает огромный интервал возможных значений амплитуд и пре вращает все их значения, доступные человеку, в значительно более узкую и удоб ную для практического использования шкалу, изменяющуюся от 0 до приблизи тельно 160. Децибелы — не такие абсолютные, фиксированные единицы, как граммы, мет ры или ватты. Выражая интенсивность звука в децибелах, мы показываем, во сколь ко раз он более интенсивен или менее интенсивен, чем звук, соответствующий эта лонному звуковому давлению Рг. Децибельная шкала, построенная относительно эталонного давления, равного 0,0002 дин/см2 и принятого в качестве порогового значения, обычно называется уровнем звукового давления (УЗД). Это название вве дено в обиход в связи с тем, что для практических целей при определении децибел нередко используются и другие эталонные давления. В табл. 12.1 представлены децибелы, рассчитанные по фор муле для интервала давлений (Ре), создаваемых некоторыми знакомыми нам ис точниками звуков. Для наглядности отобраны такие значения давлений, которые отличаются друг от друга на порядки (например, давление, равное 200 дин/см2, в десять раз больше давления, равного 20 дин/см2, которое, в свою очередь, в 10 раз больше давления, равного 2 дин/см2 и т. д.). Приведенные в таблице данные свидетельствуют о том, что изменения звуко вого давления и децибелы связаны между собой не линейной, а скорее логариф мической зависимостью. Сравнение данных, приведенных в первых двух графах, показывает, что при десятикратном увеличении звукового давления (Ре) число децибел увеличивается на 20. Например, если интенсивность одного звука равна 80 дБ, а интенсивность второго — 60 дБ, то в первом случае звуковое давление в 10 раз выше, чем во втором (разница в силе звуков равна 20 дБ). Обратите внима ние на то, что интенсивность шепота на 20 дБ превышает интенсивность звука, соответствующего слуховому порогу и имеющего интенсивность (в дБ), равную нулю. В данном случае тоже имеет место десятикратное увеличение звукового дав ления. Для сравнения: амплитуда звуковой волны, соответствующей обычному разговору, на 60 дБ больше, чем эталонный уровень, что соответствует тысячекрат ному увеличению звукового давления. Связь между звуковым давлением и децибелами (УЗД) для некоторых хорошо известных источников звуков
Нелинейный характер зависимости между изменениями звукового давления и выражениями этих изменений в децибелах требует осторожности при интерпре тации численных значений последних. Выше уже отмечалось, что увеличение зву кового давления на порядок одновременно означает и его увеличение на 20 дБ. Кроме того, двукратное увеличение звукового давления приводит к его увеличе нию на б дБ. (Аналогично и уменьшение звукового давления вдвое уменьшает ко личество децибел на б единиц.) Это значит, что если амплитуда давления звука равна 20 дБ УЗД, то после двукратного увеличения давления повышения децибельного уровня вдвое не произойдет. Скорее всего, амплитуда изменится от 20 до 26 дБ. Аналогичным образом, при уменьшении вдвое звукового давления, соответ ствующего 40 дБ УЗД, мы получим звук, интенсивность которого равна 34 дБ УЗД. Громкость — слуховое ощущение, или психологический параметр, определя емый величиной амплитуды. Звуковые волны с большими амплитудами, соответ ствующими большим изменениям звукового давления, воспринимаются как гром кие звуки, а волны с небольшими амплитудами, соответствующие незначительным изменениям звукового давления, воспринимаются как звуки малой интенсивности. Амплитуда звуковой волны важнейший, но не единственный фактор, определяю щий громкость звука. Ощущение громкости звука может зависеть также и от его частоты. Кроме того, между амплитудой и громкостью нет линейной зависимости. Как уже отмечалось выше, амплитуда звука, создающего звуковое давление, рав ное 26 дБ, в два раза больше амплитуды звука, создающего давление, равное 20 дБ; однако сказать, что первый звук в два раза громче второго, нельзя. В следующей главе этот вопрос будет рассмотрен более подробно. Сложность Большинство встречающихся в природе звуков невозможно представить простой синусоидальной волной, аналогичной той, что изображена на рис. 12.2. Звук, соот ветствующий по своим свойствам идеальной синусоиде с постоянной частотой и амплитудой, может быть получен лишь в лабораторных условиях. Большинство звуков, которые мы слышим в реальной жизни, — это сочетания акустических сиг налов, каждый из которых может быть представлен своей собственной синусоидой, вследствие чего их общая, суммарная, синусоида отличается сложностью. Так, большинство окружающих нас звуков — голоса людей и животных, шум, донося щийся с улиц, забитых транспортными средствами, звуки музыкальных инстру ментов и т. п. — это результат взаимного наложения различных волн с разными частотами. Для подобных звуков характерны чрезвычайно сложные циклы изме нений давления — циклы сжатия и разрежения (рис. 12.6).   В сложных звуковых волнах, создаваемых музыкальными инструментами, про является важное свойство источников звуковых колебаний Как правило, любой источник сложных звуковых колебаний одновременно создает звуковые волны с разными частотами. Самые низкие частоты, называемые фундаментальной часто той (или первой гармоникой), определяют высоту сложного звука Задетая скри пичная или гитарная струна колеблется как единое целое, вызывая чередование сжатий и разрежений окружающего ее воздуха Однако колебания создает не толь ко вся струна целиком (что является источником фундаментальной частоты), од новременно звуковые волны генерируются и отдельными участками струны, пред ставляющими собой строго определенные доли ее общей длины (рис. 12.7). Эти дополнительные колебания с частотами, кратными фундаментальной ча стоте, называются гармониками (или обертонами). Иными словами, фундамен тальная частота представляет собой самую низкую частоту сложной звуковой волны; все более высокие частоты, кратные частоте фундаментальной волны, пред ставляют собой гармоники последней. Роль фундаментальной частоты и ее гармо ник будет рассмотрена ниже, в разделе, посвященном патологии слуха. Сложные волны и анализ Фурье. Несмотря на то что сложный звук не может быть представлен в виде одной синусоидальной волны, его можно представить несколькими синусоидами. Вспомните то, что было сказано про анализ Фурье в главе б при обсуждении анализа сложных визуальных сцен их разложением на простые синусоидальные волны. Аналогичным образом анализируются и звуковые волны. Не вдаваясь в детали, можно сказать, что, согласно теореме Фурье, любая сложная периодическая волна может быть представлена в виде суммы ряда про стых синусоидальных волн, каждая их которых имеет свои собственные частоту и амплитуду. Разложение сложной волны любой формы на компоненты, имеющие синусоидальную форму, называется анализом Фурье. Синтез волн, имеющих сложные формы, из простых синусоидальных волн называется синтезом Фурье. В качестве примера синтеза сложной волны рассмотрим рис. 12.8. Источником приблизительно такой квадратной волны, полный цикл которой представлен в пра вом нижнем углу рис. 12.8, бывают некоторые сирены. Анализ этого звука, выпол ненный по методу Фурье, показал, что он образован пятью компонентами, пред ставленными в левой колонке рис. 12.8. Правая колонка — сложные волны, образующиеся в результате последовательного добавления компонентов (на каждом этапе добавляется по одной волне). Математически анализ Фурье начинается с фундаментальной частоты — самой низкой частоты из всех, представленных в сложной волне. Именно к ней добавляются синусоидальные волны, более высо кие частоты которых кратны фундаментальной частоте.  Высота сложного тона определяется его фундаментальной частотой. Если ис пытуемому предъявить сложный звук, а затем попросить его подобрать простой звук, соответствующий ему по высоте, то он выберет звук, который можно пред ставить простой синусоидой с частотой, примерно равной фундаментальной частоте сложного звука. Иными словами, высота сложного тона приблизительно рав на высоте звука, который можно представить синусоидой с частотой, близкой к фундаментальной частоте сложного тона (Мооге, 1994). Акустический закон Ома. Аудиальная система может, правда лишь приблизи тельно, анализировать сложные волны по методу Фурье: она разлагает их на со ставляющие компоненты и направляет информацию о представленных в ней час тотах на более высокие уровни аудиальной системы. Этот феномен, известный под названием акустического закона Ома (названного в честь немецкого физика Геор га Ома (1787-1854), более известного своими работами в области электричества заключается в следующем: когда на нас воздействует относительно сложный звук, например когда мы слышим аккорд, образованный несколькими нотами, мы спо собны оценить вклад, внесенный в него отдельно каждой нотой Иными словами, из закона Ома следует, что мы способны воспринимать индивидуальные частот ные компоненты сложного звука. Тембр. Психологическим аспектом восприятия звука, отражающим сложность звуковой волны, является тембр (от старофранцузского словаtamber, что значит «маленький колокольчик»). Тембр — это отличительное качество тона того или иного звука, являющееся результатом числа и интенсивности гармоник (или обер тонов), которые производит этот звук Например, сложный звук музыкального инструмента образован фундаментальной частотой и обертональными частотами, всегда кратными фундаментальной частоте и присутствующими в звуке в разных количествах. Количество и характер обертонов, создаваемых разными музыкаль ными инструментами, различны, вследствие чего различны и тембры. Именно бла годаря тембру мы отличаем музыкальные инструменты друг от друга даже тогда, когда звучат одни и те же ноты одинаковой высоты. Различия в тембрах музыкаль ных инструментов — следствие различий их обертонов. Подводя итог, можно сказать, что высота сложного звука зависит в первую оче редь от его фундаментальной частоты, а тембр — от гармоник. Именно поэтому такие инструменты, как гитара и фортепиано, создающие много обертонов, обла дают и более наполненным, богатым звуком, нежели инструменты, издающие от носительно чистый, однородный звук (в частности, флейта). Вопрос 2. Явление резонанса. Резкое возрастание амплитуды колебаний объекта при воздействии на него источника звука, частота которого соответствует его собственной естественной, или резонансной, частоте, называется резонансом. Резонансной или естественной называется частота, с которой колеблется приведенный в движение объект и зависит от его массы и упругости. Заставить объекты резонировать значит, вызывать колебания объектов с такой частотой, которая совпадает с частотой колебаний внешнего воздействия. Общее правило, касающееся достижения резонансной вибрации объекта, таково: чем меньше разница между резонансной частотой объекта и частотой, воздействующей на него, тем легче он достигается. То есть, наибольшие шансы вызвать резонансную вибрацию имеет источник звука, чья частота равна естественной частоте объекта. Например, когда стереосистема включена, мы можем увидеть вибрацию оконного стекла. Ее вызывают звуки, испускаемые стереосистемой, которые имеют одинаковую резонансную (или естественную) частоту со стеклом. Вопрос 3. Структура наружного уха и среднего уха (Мамаева). |
