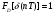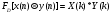Основы цифровой обработки сигнала. Вопрос. Радиотехнические сигналы. Классификация
 Скачать 1.25 Mb. Скачать 1.25 Mb.
|
|
8 Вопрос. Свертка аналогового сигнала. Свертка двух сигналов 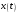 и и 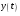 определяется как сигнал определяется как сигнал 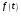 . .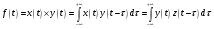 Операция свертки коммутативна, то есть при перестановке ее параметров результат не меняется. Физический смысл свертки – отклик 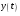 линейной аналоговой системы на входной сигнал линейной аналоговой системы на входной сигнал 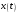 представляет собой свертку входного сигнала и импульсной характеристики системы представляет собой свертку входного сигнала и импульсной характеристики системы 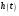 . .Преобразование Фурье от импульсной характеристики системы называется частотной характеристикой. 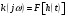
Переход от аналогового сигнала к цифровому. Квантование сигнала Дискретный сигнал представляет собой последовательность отсчета через некоторые промежутки времени. Отсчеты, как правило, берут через равный промежуток времени, называемый шагом дискретизацию. Отсчеты сигнала обычно представляется в некоторой ступенчатой форме. Ступенчатое представление сигнала называется дискретизацией. Дискретизация по времени называется выборкой. Дискретизация по уровню называется квантованием. Если сигнал, подвергнутый квантованию по времени и по значению затем представить в цифровом виде, то такое преобразование называется аналогово-цифровым преобразованием. Процесс дискретизации по уровню и по времени показан на (рис.26). 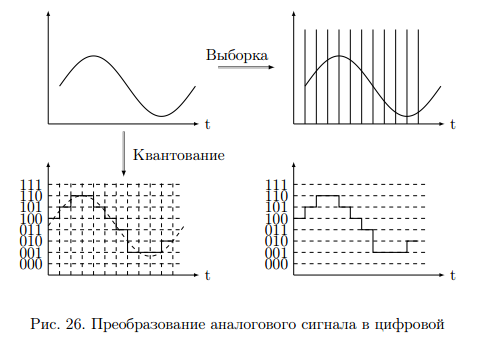 Каждому уровню аналогового сигнала ставится в соответствие двоичное число. В нашем примере мы используем 8 уровней квантования и трехразрядные двоичные числа. Таким образом мы перешли от аналогового сигнала к последовательности двоичных чисел. Цифровой сигнал существует только в дискретных во времени точках и может принимать в каждой сигнал с непрерывной амплитудой из точек только одно их 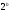 значений, где значений, где 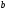 - разрядность АЦП. Процесс аналого-цифрового преобразования состоит из следующих этапов: - разрядность АЦП. Процесс аналого-цифрового преобразования состоит из следующих этапов:
Операцию дискретизации аналогового сигнала можно описать, введя в рассмотрение функцию 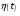 . Данная функция представляет собой последовательность . Данная функция представляет собой последовательность 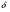 - импульсов, следующих через равные промежутки времени. - импульсов, следующих через равные промежутки времени.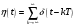 Осциллограмма функции показана на (рис. 27). 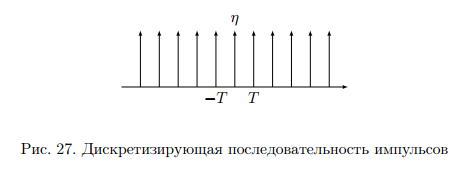 Операция перехода от аналогового сигнала к дискретному сводится к перемножению сигнала и дискретизирующей последовательности, вместо которой обычно используются остроконечные импульсы. Такая операция называется стробирование. Переходными формами от аналогового сигнала к цифровым являются сигналы с импульсной модуляцией. Импульсы могут иметь одинаковую длительность, но амплитуда может быть пропорциональна отсчетным значениям дискретизированного сигнала. Такой виз преобразования называется амплитудно-импульсной модуляцией (АИМ). Если амплитуда импульсов постоянна, а их длительность пропорциональна мгновенному значению аналогового сигнала, то получается широтно-импульсная модуляция (ШИМ). ШИМ и АИМ сигнала показаны на (рис. 28). 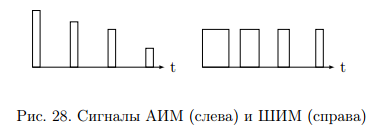 10 Вопрос. Теорема Котельникова (Найквиста) Возникает задача: какой же максимальный интервал выборки нужен, чтобы по отсчетам можно было восстановить первоначальную форму сигнала? Если 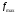 - самый высокочастотный компонент сигнала, то чтобы элементы выборки полностью описывали сигнал, дискретизация сигнала должна осуществляться с частотой - самый высокочастотный компонент сигнала, то чтобы элементы выборки полностью описывали сигнал, дискретизация сигнала должна осуществляться с частотой 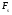 не ниже не ниже 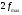 . .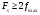 . .Смысл теоремы Котельникова иллюстрирует (рис. 29). 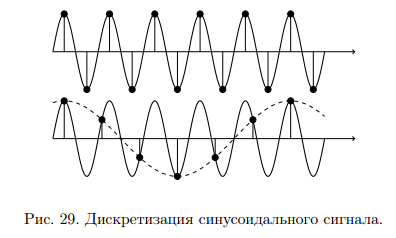 Как видно из рисунка, если частота дискретизации равна удвоенной частоте синусоидального сигнала, что по полученным отсчетам можно восстановить исходный сигнал. Если частоту дискретизации выбрать меньшей, что частота сигнала, восстановленного по отсчетам будет меньше, чем у исходного сигнала и восстановленный сигнал можно будет принять за более низкочастотный. Данное явление называется наложением. Спектр дискретного сигнала и наложения Спектр дискретного сигнала представляет собой сумму бесконечного числа копий спектра исходного сигнала. Каждая копия спектра аналогового сигнала сдвинута по оси частот на расстояние, равное частоте дискретизации. 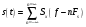 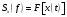 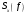 - спектр цифрового сигнала - спектр цифрового сигнала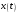 - исходный сигнал - исходный сигналСпектры аналогового и цифрового сигналов показаны на (рис. 30). 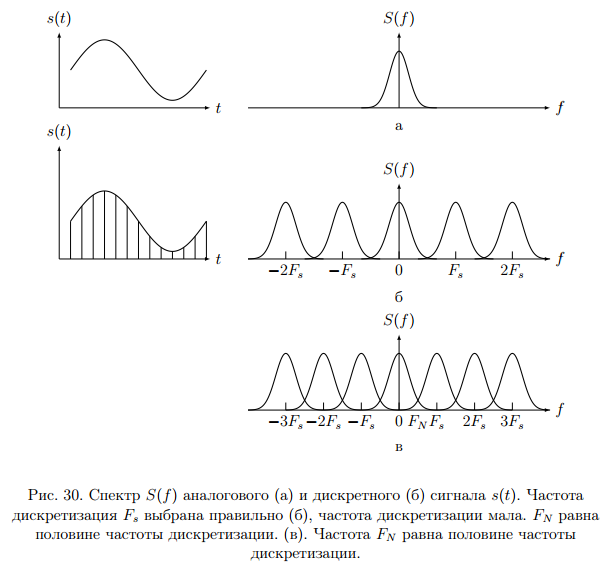 Видно, что:
Для борьбы с наложением можно либо ограничивать полосу частот сигнала, пропуская его через ФНЧ, либо повышать частоту дискретизации, чтобы отодвинуть по оси частот спектр сигнала и зеркальный спектр дальше друг от друга. 11 Вопрос. Восстановление сигнала по отсчету Из (рис. 30) видно, что чтобы восстановить исходный аналоговый сигнал по отсчету, нужно пропустить дискретный сигнал через ФНЧ. При этом зеркальный спектр подавится, а главный лепесток спектральной диаграммы пройдет через ФНЧ. Так как идеальный ФНЧ реализовать невозможно, то на выходе ФНЧ всегда будут присутствовать компоненты зеркальных частот. Поэтому полностью восстановить сигнал по отсчетам невозможно. Простейшим ФНЧ является интегрирующая 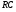 цепочка. Процесс восстановления сигнала при помощи интегрирующей цепочка. Процесс восстановления сигнала при помощи интегрирующей 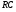 цепочки показан на (рис. 31). цепочки показан на (рис. 31). 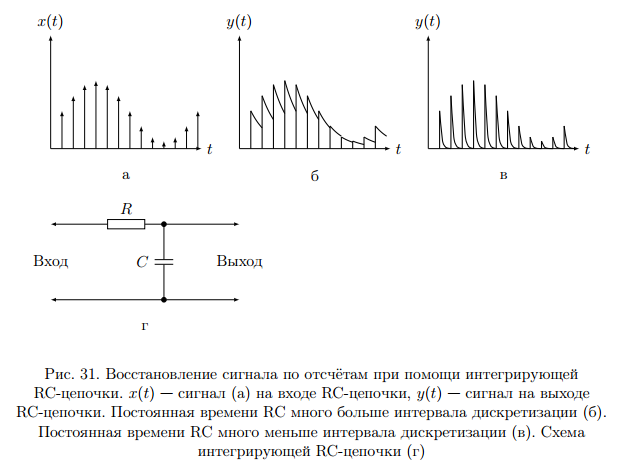 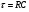 - постоянная времени - постоянная времени 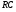 цепочки. цепочки.Ошибки квантования При АЦП сигнал описывается 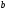 двоичными разрядами. Квантование вносит ошибку, которая является функцией разрядности АЦП. двоичными разрядами. Квантование вносит ошибку, которая является функцией разрядности АЦП.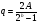 - шаг квантования. - шаг квантования. 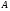 - входной диапазон АЦП. - входной диапазон АЦП.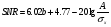 - отношение сигнал/шум. - отношение сигнал/шум.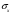 - среднеквадратичное значение сигнала (RMS). - среднеквадратичное значение сигнала (RMS).Для синусоидального сигнала 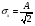 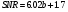 Дб ДбПусть двухполярная АЦП. 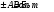 ; B = 16 бит ; B = 16 бит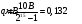 SNR = 98 дБ; q/2 = 76 дБ 12 Вопрос. Система цифровой обработки сигналов реального времени Структурная схема СЦОС реального времени показана на (рис. 32). 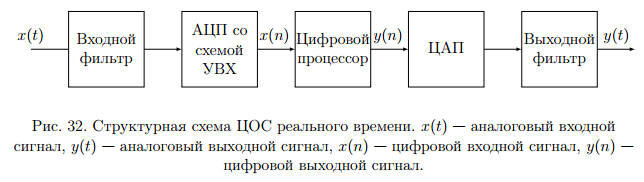 Аналоговый входной фильтр используется для ограничения полосы частот входного сигнала перед его оцифровкой. АЦП преобразует аналоговый сигнал в цифровую форму. Если у сигнала широкая полоса частот или применяется низкоскоростное АЦП, то перед оцифровкой нужно воспользоваться схемой выборки хранения (УВХ). Поле цифровой обработки в процессоре сигнал преобразуется в аналоговую форму при помощи ЦАП. Выходной фильтр сглаживает выходной сигнал после ЦАП и устраняет высокочастотные компоненты. Главный компонент – цифровой сигнальный процессор. Его можно использовать как обычный универсальный, так и как специальный процессор ЦОС. Спектральный анализ дискретных сигналов 13 Вопрос. Дискретное преобразование Фурье ДПФ (DFT) Преобразование Фурье нельзя применить к дискретному сигналу. Для спектрального анализа дискретного и в том числе цифрового сигнала служит ДПФ. Предположен, что сигнал дискретизирован через равные промежутки времени Т и получена дискретная последовательность из 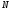 выборок. выборок.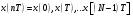 ДПФ можно определить, как последовательность комплексных значений в частотной области. 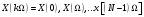 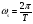 - частота дискретизации. - частота дискретизации.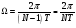 Значения ДПФ вычисляются следующим образом: 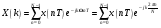 Данное выражение называется прямым ДПФ. При вычислении ДПФ последовательность из N действительных значений в действительной области преобразуется в последовательность из N комплексных значений в частотной области. Переход к безразмерной частоте дискретизации: 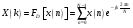 ДПФ представляет дискретный сигнал в виде суммы синусоидальных сигналов с круговыми частотами, кратными 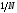 . .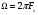 Связь ДПФ с преобразованием Фурье 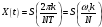 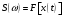 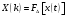 Графически связь между спектром и ДПФ дискретного сигнала показана на (рис. 33). 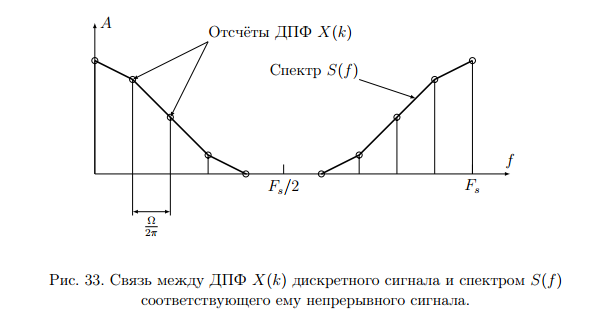 Спектральные отсчеты расположены на оси частот от 0 до 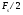 и в них заключена вся информация о составе сигнала. Правая часть ДПФ на оси частот от и в них заключена вся информация о составе сигнала. Правая часть ДПФ на оси частот от 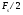 до до 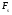 соответствует отрицательным частотам и не несет дополнительной информации о сигнале. соответствует отрицательным частотам и не несет дополнительной информации о сигнале. Восстановление исходного сигнала из ДПФ. Если известна последовательность коэффициентов ДПФ X(k), которая была найдена по последовательности отсчетов X(n), то по ним может быть найден исходный сигнал x(t), который был подвергнут дискретизации. Выражение для исходного сигнала с учетом симметричного ДПФ: 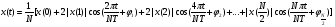 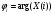 - фаза соответствующего спектрального отсчета - фаза соответствующего спектрального отсчета|X(i)| - амплитуды спектра. Пример восстановленного сигнала показан на рисунках 36, 37. 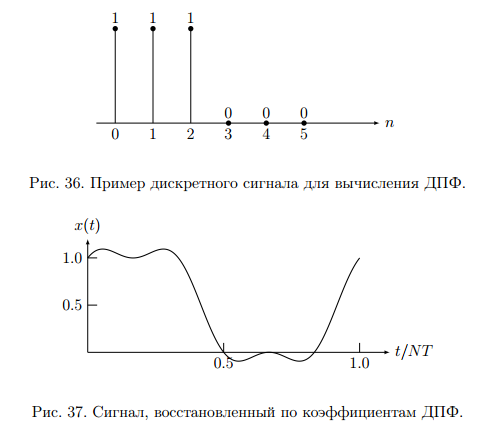 14 Вопрос. Дискретная свертка Дискретной сверткой двух последовательностей 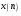 и и 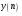 называют последовательность называют последовательность 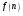 , каждый элемент которой равен: , каждый элемент которой равен: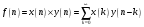 Дискретная свертка вводится по аналогии со сверткой двух аналоговых сигналов. Различают линейную и круговую дискретные свертки. В случае круговой свертки предполагается, что дискретные сигналы периодические с одинаковым периодом N отсчетов. 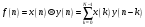 С помощью круговой свертки можно вычислить линейную свертку. Для этого нужно каждую из последовательностей 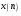 длиной N отсчетов и длиной N отсчетов и 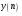 длиной M отсчетов дополнить нулями до M=N-1 отсчетов. длиной M отсчетов дополнить нулями до M=N-1 отсчетов.Пример вычисления линейной свертки показан на (рис. 34).  На рисунке 34 утолщенной линией показана граница повторения периодических сигналов. На каждом шаге вычисляется круговая свертка, сигнал сдвигается циклически и последний отсчет заступает на место первого. 15 Вопрос. Свойства ДПФ:
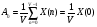
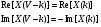
Теорема устанавливает равенство 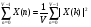 Операция свертки во временной области соответствует операции умножения в частотной области. Пример смотри в методических указаниях к семинару №3. Обратное ДПФ. Обратное ДПФ позволяет перейти от частотной области во временную. 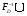 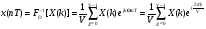 Обратное дискретное преобразование Фурье позволяет переходить от спектра к сигналу. При этом можно вычислить круговую свертку: 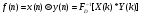  16 Вопрос. Быстрое преобразование Фурье. Для вычисления ДПФ от сигнала из N – отсчетов необходимо провести 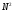 операций с комплексными числами. Каждому из отсчетов сигнала ставится в соответствие элемент спектра, на вычисление которого необходимо N операций. Вычисление по такому алгоритму для больших массивов требует значительных затрат машинного времени. операций с комплексными числами. Каждому из отсчетов сигнала ставится в соответствие элемент спектра, на вычисление которого необходимо N операций. Вычисление по такому алгоритму для больших массивов требует значительных затрат машинного времени.БПФ (FFT) служит для преодоления этого недостатка. Для вычисления БПФ требуется порядка 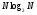 операций, массив, содержащий операций, массив, содержащий 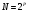 отсчетов, Р – целое число. Если входной массив не укладывается в такую размерность, то его дополняют нулями. Если при вычислении ДПФ заменить вычисление одного ДПФ для массива из N элементов на вычисление 2х ДПФ для массива из N/2 элементов, объем увеличится в 2 раза. отсчетов, Р – целое число. Если входной массив не укладывается в такую размерность, то его дополняют нулями. Если при вычислении ДПФ заменить вычисление одного ДПФ для массива из N элементов на вычисление 2х ДПФ для массива из N/2 элементов, объем увеличится в 2 раза.Исходный массив разбивают до тех пор, пока не дойдут до массива из 2х элементов. Для такого массива вычисляют ДПФ по определению. Чтобы перейти к исходной длине массива существуют алгоритмы объединения. Схемотехнически, данный алгоритм показан на рис. 38. 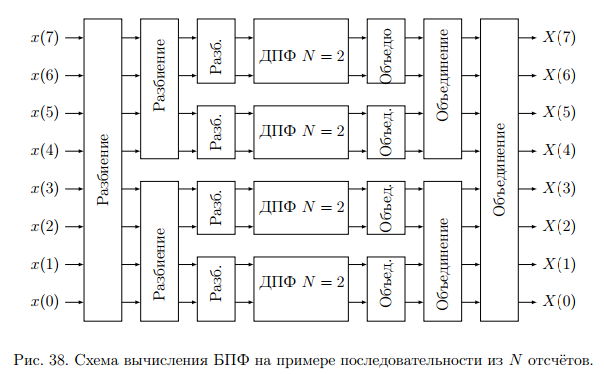 Одним из алгоритмов вычисления БПФ является алгоритм с прореживанием по времени. Структурная схема алгоритма с прореживанием по времени – рис.40. 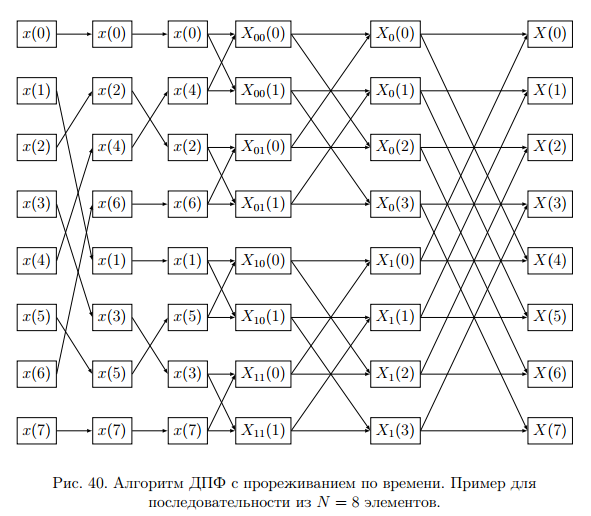 Операция объединения в данном алгоритме выполняется на основе поворотных коэффициентов. Процесс объединения схемотехнично показан на рис.39. 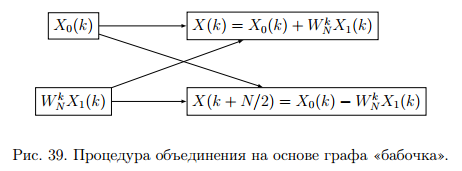 Подробное описание алгоритма смотри в методическом указании семинара №3. 17 Вопрос. Оконные функции. Для вычисления ДПФ используют отрезки сигналов конечной длины. Оконные функции служат для выборки отрезка сигнала конечной длины из бесконечного сигнала. Оконная функция равна 0 за пределами отрезка времени и не равна 0, в его пределах. Чтобы ограничить во времени дискретный сигнал его надо умножить на оконную функцию. Также оконные функции устраняют размытие пиков на спектре диаграммы в результате неправильного выбора fs и количества отсчетов. Умножение сигналов производится следующим образом: 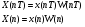 ДПФ для сигнала с окном: 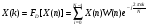 В данном выражении каждый из отсчетов сигнала домножается на весовые коэффициенты, определяющие функцию окна. Простейшая оконная функция – прямоугольное окно. Оно получается автоматически при выборке из сигнала отрезка длиной N-отсчетов. Значение оконной функции равно 1 в пределах окна, и 0 за его пределами. 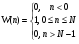 Прочие окна домнажаются каждый отсчет сигнала на весовой коэффициент, зависящий от № отсчета. Окно Хэмминга: 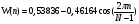 Часто используют окна Кайзера, Блэкмана и Ханна. На рисунке 43 показано взаимодействие окна Хэмминга на амплитудный спектр сигнала. 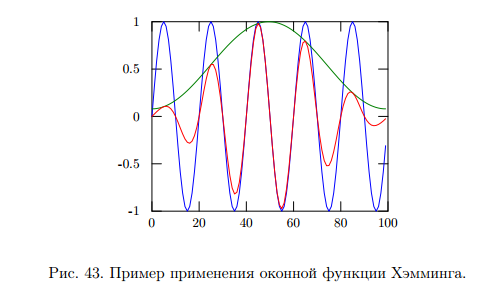 Если использовать прямоугольное окно, то наблюдается размытие пиков спектра. В хвостах пиков содержится ложная информация и можно ошибочно заключить, что в спектре дополнительно присутствуют сигналы. Если использовать окно Хэмминга, то пики становятся острее и ложная информация отсекается. |

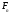 равная половине частоты дискретизации -
равная половине частоты дискретизации - 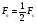 называется частотой Найквиста. В данной точке (на данной частоте) происходит наложение. Так же данную частоту называют максимальной частотой сигнала.
называется частотой Найквиста. В данной точке (на данной частоте) происходит наложение. Так же данную частоту называют максимальной частотой сигнала.