Основы цифровой обработки сигнала. Вопрос. Радиотехнические сигналы. Классификация
 Скачать 1.25 Mb. Скачать 1.25 Mb.
|
|
Основы цифровой обработки сигнала (ОЦОС). Преподаватель: Кузнецов Вадим Вадимович Https://github.com/ra3xdh/DSP-RPD Https://github.com/ra3xdh/RTUiS-labs
Сигналом называют процесс изменения во времени физического состояния какого-либо объекта, который служит для отображения, регистрации и передаче сообщений. Сигналами могут быть напряжение, ток, напряженность поля. В большинстве случаев носителями радиотехнических сигналов являются электромагнитные колебания. Математической моделью сигнала обычно служит функциональная зависимость аргументом которой является время (зависимость напряжения в цепи от времени). Для детерминированных сигналов на основании математической модели можно узнать мгновенное значение сигнала в любой момент времени. Примером детерминированного сигнала является синусоидальное напряжение, 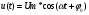 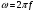 f=50Гц w=314с^-1. f=50Гц w=314с^-1.Для случайного сигнала рассчитать значение согласно математической модели невозможно. Примером случайного сигнала является белый шум. Осциллограмма белого шума показана на рисунке 1.  Импульсные сигналы существуют только в пределах конечного отрезка времени. Примеры импульсных сигналов: видеоимпульс (рис. 2а) и радиоимпульс (рис.2б).  Если физический процесс порождающий сигнал развивается во времени таким образом, что его можно измерять в любые моменты времени, то сигналы такого класса называют аналоговым. Аналоговый сигнал можно представить графиком его изменения во времени, то есть осциллограммой. Дискретные сигналы описываются совокупностью отсчетов через равные промежутки времени. Пример дискретного сигнала показан на рисунке 3.  Цифровые сигналы являются особой разновидностью дискретных. Отсчетные значения представляются в виде чисел. Обычно используются двоичные числа с некоторой размерностью. Пример цифрового сигнала приведен в таблице 1.  Аналоговые сигналы. Периодический сигнал S(t), период Т обладает следующим свойством: S(t)=S(t±nT) n=1,2,.. Пример периодического сигнала показан на рисунке 4. 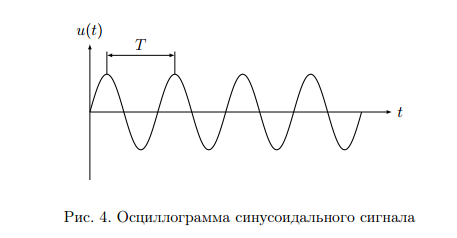 Период сигнала связан с частотой f и круговой частотой w следующим соотношением: f=1/T=w/2π. Другие примеры периодических сигналов показаны на рисунке 5. 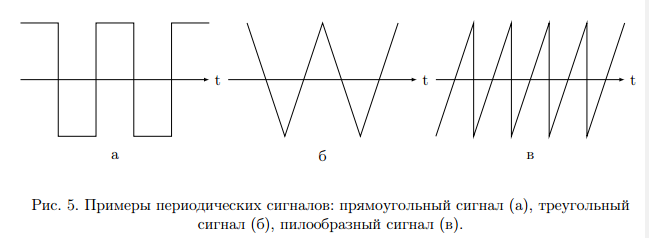
Для передачи низкочастотным сигналов, например звуковых, по радиоканалу применяются модулированные сигналы. Прямая передача низкочастотного сигнала по радиоканалу невозможна, так как длинна волны для низких частот слишком большая и аппаратура для передачи такой волны будет громоздкой. В модулированном сигнале амплитуда, частота и фаза синусоидального ВЧ сигнала изменяется в такт с НЧ. НЧ сигнал накладывается на несущий. 1. Амплитудная модуляция (АМ). 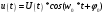 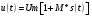 S(t) - звуковой сигнал, 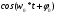 - РЧ сигнал, несущая, М - коэффициент модуляции. - РЧ сигнал, несущая, М - коэффициент модуляции.Пример модулированного сигнала показан на рисунке 6. 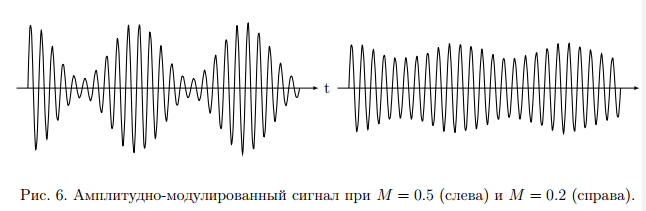 2. Частотная модуляция (ЧМ:FM). Амплитуда несущий остается неизменной, а в такт с модулируемым сигналом изменяется частота несущей. 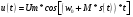 Осциллограмма частотно-модулированного сигнала показана на рисунке 7. 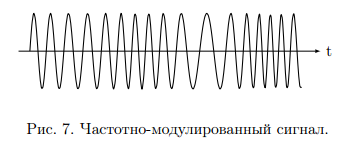 3. Фазовая модуляция (ФМ:PM). 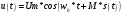 . осциллограмма ФМ сигнала показана на рисунке 8. . осциллограмма ФМ сигнала показана на рисунке 8. 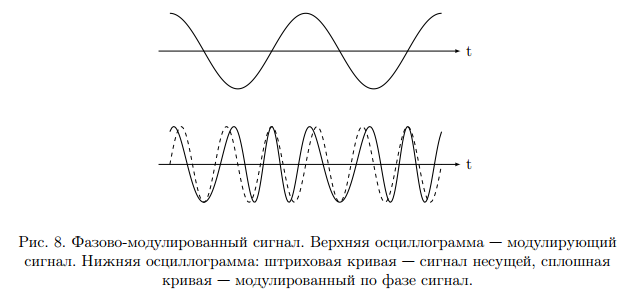 Во время положительного полупериода фаза модулированные колебания опережают по фазе колебания несущей частоты, при этом период колебаний уменьшается, и частота увеличивается. Во время отрицательного периода модулирующего напряжения фаза модулированного колебания отстает по фазе от колебаний несущей частоты. Таким образом ФМ является одновременно и ЧМ. Для ЧМ справедливо обратное суждение: частотная модуляция является одновременно фазовой модуляцией. ФМ применяется в профессиональной радиосвязи. Сигма и дельта функции. Сигма функция задается следующим выражением: 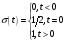 (рис. 9) (рис. 9)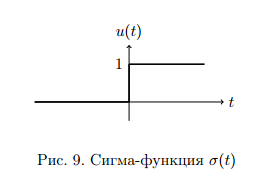 Дельта функция – импульс бесконечно большой амплитуды и бесконечно малой длительности. (рис. 10). 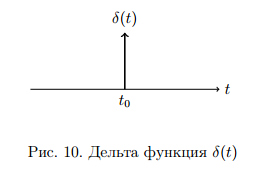 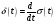 - дельта-функция является производной от сигма-функции. - дельта-функция является производной от сигма-функции.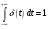 Если сигнал, задаваемый непрерывной функцией умножить на дельта-функции и проинтегрировать во времени, то результатом будет мгновенное значение сигнала в точке, где сосредоточен дельта-импульс. 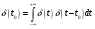 Из фильтрующих свойств дельта-функции следует схема измерителя мгновенного значения сигнала. Сигма и дельта функции применяются для анализа прохождения аналоговой и цифровых сигналов через линейные системы. Отклик системы, ели на нее подан дельта-импульс, называется импульсной характеристикой системы H(t).
Мощность выделяющаяся на резисторе сопротивлением R, если к нему приложено напряжение u определяется как W=(u^2)/R. Если к резистору приложено не постоянное напряжение, а переменный сигнал s(t), то мощность так же будет переменной (мгновенная мощность). В теории сигналов обычно полагают, что R=1. w=s(t) ^2. Чтобы найти энергию сигнала необходимо проинтегрировать мощность по всему диапазону; 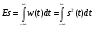 Для бесконечных во времени сигналов среднюю мощность можно определить следующим образом: 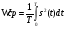 W=[Вт], E=[(В^2)*c] Именно такая энергия выделяется на резисторе сопротивлением 1 ом, если к нему приложено напряжение s(t). Если сигнал излучается на некотором интервале T, то рассматривается средняя мощность сигнала. Спектральный анализ сигналов.
Разложение в ряд Фурье заключается в представление периодического сигнала в виде суммы синусоидальных сигналов. Пример представления пилообразного сигнала в виде суммы синусоидальных сигналов с различной амплитудой и фазой представлен на рис. 12. 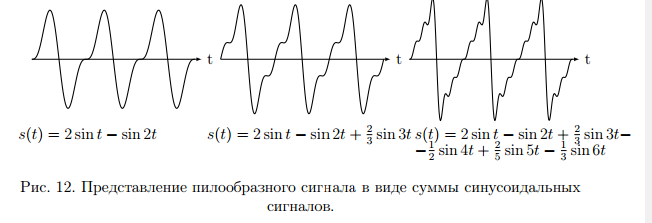 Введем основную частоту периодического сигнала с периодом T: w_1=2pi/T. Периодический сигнал при разложении в ряд Фурье представляется в виде суммы синусоидальных сигналов или гармоник, с частотами кратными основной частоте: 2w_1, 3w_1... Амплитуды этих сигналов называются коэффициентами разложения. Ряд Фурье записывается в виде суммы гармоник: 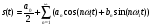 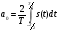 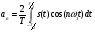 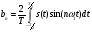 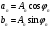 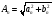 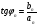 Вещественная форма ряда Фурье: 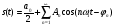 Используя известную форму записи из курса электротехники в виде комплексного числа, ряд Фурье представляется в виде: 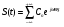 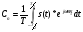 В данное выражение входят гармоники с отрицательными частотами. Отрицательная частота – это не физическое понятие, она связана со способом представления комплексных чисел. Так как сумма гармоник должна быть действительным числом, то каждой гармонике соответствует комплексно сопряженная гармоника с –ω. По абсолютному значению амплитуды гармоники с положительными и отрицательными частотами равны.
Спектральные диаграммы – графики, изображающие коэффициенты ряда Фурье в вещественной форме. Различают амплитудные и фазовые спектральные диаграммы. По горизонтальной оси откладывают частоты гармоник, по вертикали – амплитуды (фазы). Если изображен модуль ряда Фурье в комплексной форме, то по оси Х откладывают положительную и отрицательную круговую частоту ω. Пример спектра аналогового периодического сигнала. (ШИМ) Рассмотрим последовательность прямоугольных импульсов с периодом Т, длительностью τ и амплитудой А. 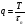 - скважность. - скважность.Осциллограмма такого сигнала оказана на рисунке 13. 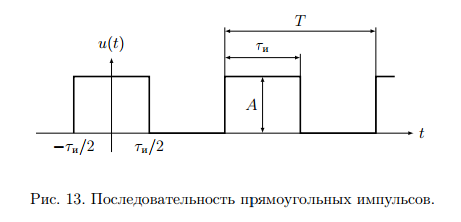 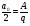 - постоянная составляющая прямоугольного сигнала. - постоянная составляющая прямоугольного сигнала.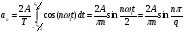 bn = 0. bn = 0.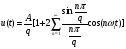 Спектральная диаграмма для последовательности прямоугольных импульсов показана на рис. 14. 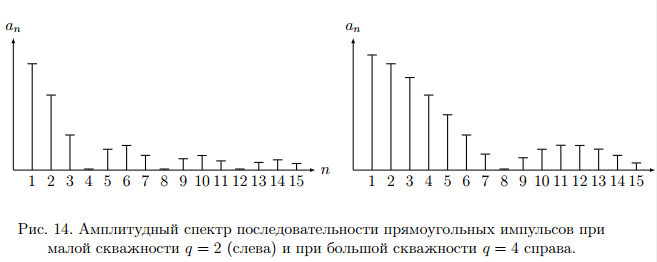 Из спектра диаграммы видно, что с увеличением скважности уменьшается длительность импульса. Последовательность прямоугольных импульсов имеет более богатый спектральный состав, в спектре присутствуют больше гармоник и больше амплитуд. Таким образом, сокращение длительности импульса приводит к расширению спектра. Сигналы с широким спектром могут создавать помехи. Вычисление ряда Фурье производится с помощью математических пакетов. Преобразование Фурье. Применяется для расширения области допустимых сигналов. Различают прямое и обратное преобразование.
Разложение в ряд Фурье позволяет получить спектр только для периодических сигналов. Преобразование Фурье расширяет область применения спектрального анализа на непериодические сигналы. Пусть s(t) – одиночный импульсный сигнал конечной длительности. Дополним его таким же, периодически следующим сигналом, с периодом Т. Получим последовательность импульсов (рис.15). 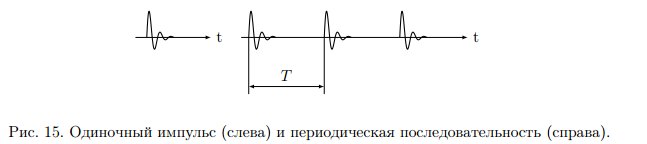 Чтобы перейти к преобразованию Фурье и найти спектр одиночного импульса необходимо найти предельный вид ряда Фурье в комплексной форме при 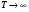 Расчет спектра: 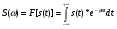 Физический смыл спектральной плотности состоит в том, что она является коэффициентом пропорциональности между длинной малого интервала частот Δf в близи частоты f0 и амплитуды гармонического сигнала с частотой f0. Сигнал s(t) как бы складывается из множества разных синусоидальных сигналов малой амплитуды. Спектр плотности показывает вклад в сигнал элементарных синусоидальных сигналов каждой частоты. Спектр плотности вероятности 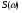 является комплексным числом и отображается кривой на комплексной плоскости. является комплексным числом и отображается кривой на комплексной плоскости.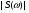 - действительное число – амплитудный спектр - действительное число – амплитудный спектр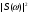 - спектр мощности - спектр мощности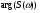 - фазовый спектр - фазовый спектрСвойства преобразования Фурье
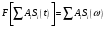
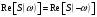 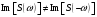
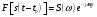
Спектр произведения сигналов равен свертке спектров и наоборот. 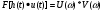 Свойство применяется для отыскания сигнала на выходе, если известна АЧХ. 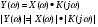 Линейная система и сигналы на ее входе и выходе показаны на рисунке 20. 
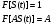 В спектре дельта-импульса содержатся все частоты от 0 до 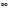 . .
Дифференциация сигналов приведет к расширению спектра, интегрирование – к сжатию (рис.21). 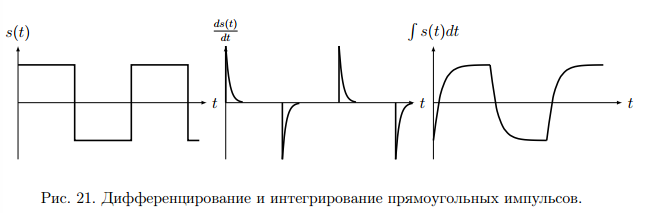
Комплексная амплитуда 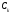 к-ой гармоники ряда Фурье связана со спектральной плотностью так: к-ой гармоники ряда Фурье связана со спектральной плотностью так: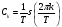 Зная преобразование для одного периода периодического сигнала можно вычислить его разложение в ряд Фурье. Пример вычисления спектра импульсного сигнала. Вычислим спектр прямоугольного видео импульса 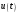 с амплитудой с амплитудой 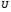 и длительностью и длительностью 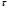 . Импульс расположен симметрично относительно начала отсчета (рис. 22). . Импульс расположен симметрично относительно начала отсчета (рис. 22).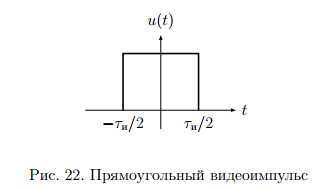 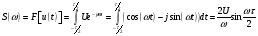 Переходим от круговой частоты к частоте f. 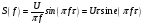 Амплитудный спектр показан на (рис 23). 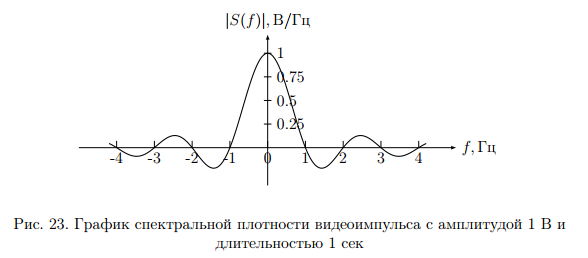 Фазовый спектр показан на (рис 24).  Спектр мощности показан на (рис 25). 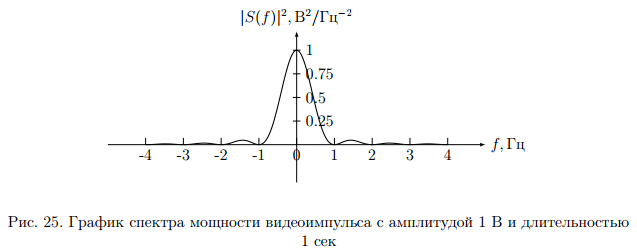
Служит для нахождения сигнала по спектру. 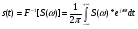 Условие существования спектральной плотности сигнала. Спектральный анализ интегрируемых сигналов. Сигнал 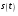 можно сопоставить спектральную плотность можно сопоставить спектральную плотность 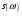 если сигнал абсолютно интегрирован. если сигнал абсолютно интегрирован.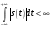 К абсолютно интегрированному сигналу не относятся гармонические колебания и постоянный ток. Примеры абсолютно интегрируемых и неинтегрируемых сигналов на (рис. 16).  Спектры таких сигналов представляются через дельта-функции. Спектр сигнала постоянного уровня А представляет собой дельта-импульс, расположенный на нулевой частоте ( 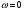 ). ).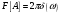 Физический смысл данного выражения – сигнал, постоянный по модулю и по времени имеет постоянную составляющую только на нулевой частоте. 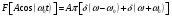 - спектр синусоидального сигнала. - спектр синусоидального сигнала.Любой периодический сигнал можно представить рядом Фурье в комплексной форме, то есть в виде суммы синусоидальных сигналов. 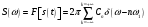 Спектры постоянного тока, синусоидального и периодического сигнала показаны на (рис. 17). 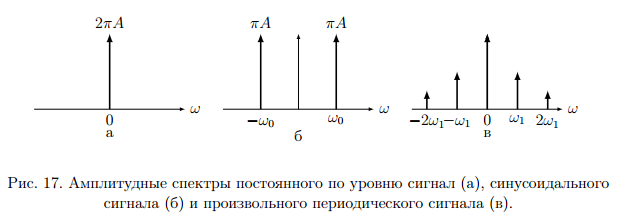 На анализаторе спектра спектр периодического сигнала будет наблюдаться в виде последовательности остроконечных импульсов. Амплитуды данных импульсов пропорциональны амплитудам гармоник. Типичный вид спектра представлен на (рис. 18).  Спектральный анализ можно применять и к случайным сигналам. Для них рассматривается спектр мощности 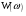 . Для примера рассмотрим белый шум (рис. 1). . Для примера рассмотрим белый шум (рис. 1). Белый шум имеет равномерный спектр, то есть выполняется условие 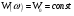 . . |