Основы цифровой обработки сигнала. Вопрос. Радиотехнические сигналы. Классификация
 Скачать 1.25 Mb. Скачать 1.25 Mb.
|
|
18 Вопрос. Цифровые фильтры. Системы дискретного времени. Системы дискретного времени – систематические алгоритмы, на входе которых последовательность двоичных чисел x(t), а на выходе – последовательность двоичных чисел y(t). Пример системы ДБ – цифровой фильтр. Система дискретного времени может быть линейной и нелинейной, инвариантной относительно времени и изменятся во времени. Система линейна, если она подчиняется принципу суперпозиции. 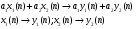 Система дискретного времени инвариантна относительно времени, если ее параметры не зависят от времени, то есть если вход x(t) дает выход y(t), то вход x(t)-k дает выход y(t)-k, то есть задержка входного сигнала приведет к такой задержке выходного. Взаимосвязь между входами и выходами линейной системы задается сверткой: 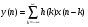 , где h(k) – импульсная характеристика. , где h(k) – импульсная характеристика.Импульсная характеристика системы – отклик системы на единичный импульс. Значение единицы импульса 1 при n=0, u=0 при остальных n. 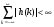 2 класса системы: 1) конечная импульсная характеристика (КИХ), то есть импульсная характеристика конечной длинны; 2) БИХ системы с импульсной характеристикой бесконечной длинны. 19 Вопрос. Z – преобразование. Определяется следующим образом: 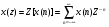 , где z – комплексная переменная для системы , где z – комплексная переменная для системы 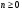 Z – преобразование – степенной ряд u имеет область сходимости, в которой x(z) – конечная. 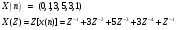 Обратное Z – преобразование позволяет восстановить последовательность по ее z – образу. 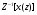 Z – образ можно разложить в степенной ряд: 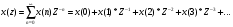 Из данной записи видно, что коэффициенты можно найти как 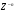 . X(Z) выражается как отношение 2-х многочленов: . X(Z) выражается как отношение 2-х многочленов: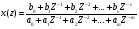 Обратное Z – преобразование может найти отличие 3-х методов: метода разложения в степенной ряд, метод разложения на элементарные дроби, метод вычетов. Рассмотрим последний метод. 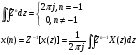 Свойства Z – преобразования:
Z – преобразование от сигнала y(t) получена из исходного сигнала x(t) сдвигом на одну позицию в сторону запаздывания, равную Z – преобразованию исходного сигнала, домноженного на 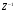 . .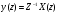 , где , где 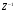 - задержка на длину интервала дискретизации. - задержка на длину интервала дискретизации.
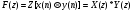 20 Вопрос. Прохождение цифрового сигнала через систему ДВ. Система ДВ характеризуется передаточной характеристикой h(z): 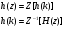 На основании свойств Z – преобразования: 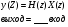 Передаточная функция определяет частными свойствами системы ДВ. 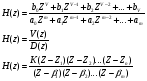 k- коэффициент усиления, Zn – нули (корни числителя), βm – полюса (корни знаменателя). Нули и полюса применяются для исследования частотных характеристик. 21 Вопрос. Цифровые фильтры с конечной импульсной характеристикой (КИХ). Физически осуществимые цифровые фильтры работают в реальном масштабе времени, для формирования выходного сигнала в i-ый дискретный момент времени могут использовать следующие данные:
Целые числа m и n определяют порядок цифрового фильтра. Фильтры классифицируются в зависимости от того, как используется информация о прошлом состоянии системы. Фильтры с КИХ или не рекурсивные фильтры, работающие в соответствии со следующим алгоритмом. 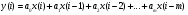 , m – порядок фильтра. , m – порядок фильтра.Не рекурсивный фильтр производит взвешивание, суммирование предыдущих отсчётов входного сигнала. Прошлые отсчеты выходного сигнала не используются. 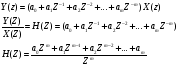 H(z) – системная функция. Системная функция имеет m нулей и один полюс, при z=0. Алгоритм функционирования цифрового фильтра с КИХ показан на рис.45. 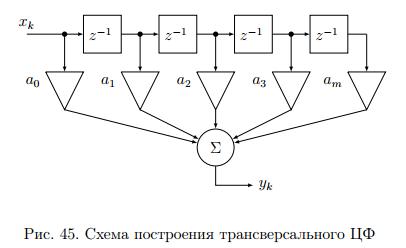 Основными элементами фильтра служат блоки задержки отсчетов значений на 1 интервал дискретизации 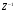 . .Масштабные блоки, выполняющие умножение на весовые коэффициенты в цифровой форме. С выхода масштабных блоков сигнал поступает в сумматор, где вычисляется выходной сигнал. Данная структурная схема не является электрической, а служит графическим изображением алгоритма обработки сигнала на ЭВМ. Выходными и входными данными для такого алгоритма служат массивы чисел. Применим к системным функциям обратное Z – преобразование и найдем импульсную характеристику: 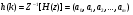 (импульсная характеристика фильтра). (импульсная характеристика фильтра).Импульсная характеристика КИХ фильтра содержит конечное число элементов и данный фильтр всегда устойчив. Найдем частотную характеристику выполнив подстановку 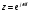 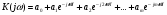 T=1/fs – интервал дискретизации. Подбирая коэффициенты  в данном выражении можно получить АЧХ фильтра. в данном выражении можно получить АЧХ фильтра.Пример программной реализации ЦФ с КИХ – семинар №4. 22 Вопрос. Рекурсивный фильтр (БИХ). Отличатся тем, что используются значения не только входного сигнала, но также и значения своего выходного сигнала для конечного выходного сигнала. 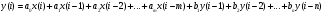 bn – коэффициенты рекурсивной части,  одновременно. одновременно.Применим Z – преобразование и рассчитаем системную функцию: 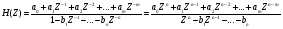 Структурная схема рекурсивной части ЦФ показана на рисунке 46. 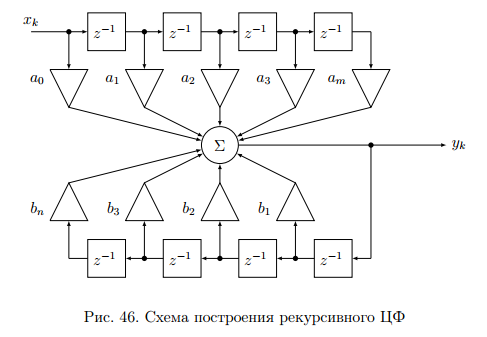 Верхняя часть схемы соответствует не рекурсивной части алгоритма фильтрации. Нижняя часть схемы реализует рекурсивную часть алгоритма. Так как в алгоритме имеются обратные связи, то фильтр имеет БИХ. Приведем выражение для импульсной характеристики ЦФ 1-ого порядка. 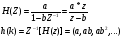 Импульсная характеристика вычисляется методом вычетов и представляет собой убывающею геометрическую прогрессию. Рекурсивные ЦФ имеют как правило аналоговый фильтр прототип а АЧХ Чебышева, Батерворта, Кауэра. Так как рекурсивный фильтр имеет БИХ, то он может быть неустойчивым. Практически могут применятся только устойчивые фильтры. 23 Вопрос. Канонический рекурсивный фильтр. Предназначен для оптимизации использования памяти рекурсивным алгоритмом фильтрации. Использует минимальное возможное число ячеек памяти (максимальное из числе m и n). Структурная схема фильтра показана на рис. 47. 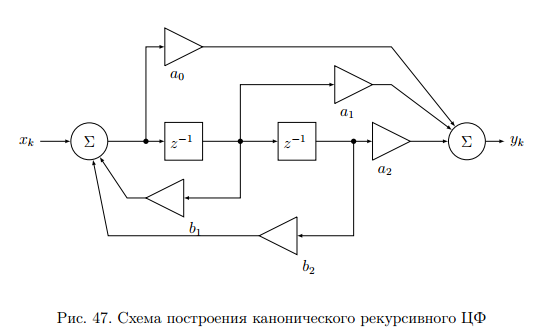 На рисунке изображен фильтр 2-ого порядка, системная функция которого равна: 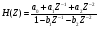 24 Вопрос. Синтез ЦФ. Метод инвариантных импульсных характеристик. Задачей синтеза являются поиски значений коэффициентов a и b цифрового фильтра. В основе данного метода лежит предположение, что синтезированный ЦФ должен обладать импульсной характеристикой, которая является результатом дискретизации соответствующей импульсной характеристики аналогового фильтра – прототипа.  Число элементов импульсной характеристики может быть конечным или бесконечным. Это определяет структуру синтезируемых фильтров. Связь между коэффициентами импульсной характеристики и структур фильтра наиболее проста для нерекурсивного фильтра. Синтез осуществляется путем применения z - преобразования к h(k). Все приближения к АЧХ аналогового фильтра прототипа зависит от выбранного шага дискреции. При необходимости можно вычислить частотный коэффициент передачи и по нему АЧХ выполнив подстановку  . .25 Вопрос. Синтез ЦФ. Метод инвариантных частотных характеристик. Принципиально невозможно создать ЦФ, частотная характеристика которого в точности повторяла бы частотную характеристику некоторой аналоговой цепи. Причина состоит в том, что частотный коэффициент передачи ЦФ является периодической функцией частоты с периодом, определяемым шагом дискретизации. Подобие (инвариантность) частотных характеристик аналогового и цифрового фильтров, заключается в том, что весь бесконечный интервал частот wa аналоговой системы, был преобразован в отрезок частот wч ЦФ в интервале [-π/T; π/T] при сохранении общего вида АЧХ. 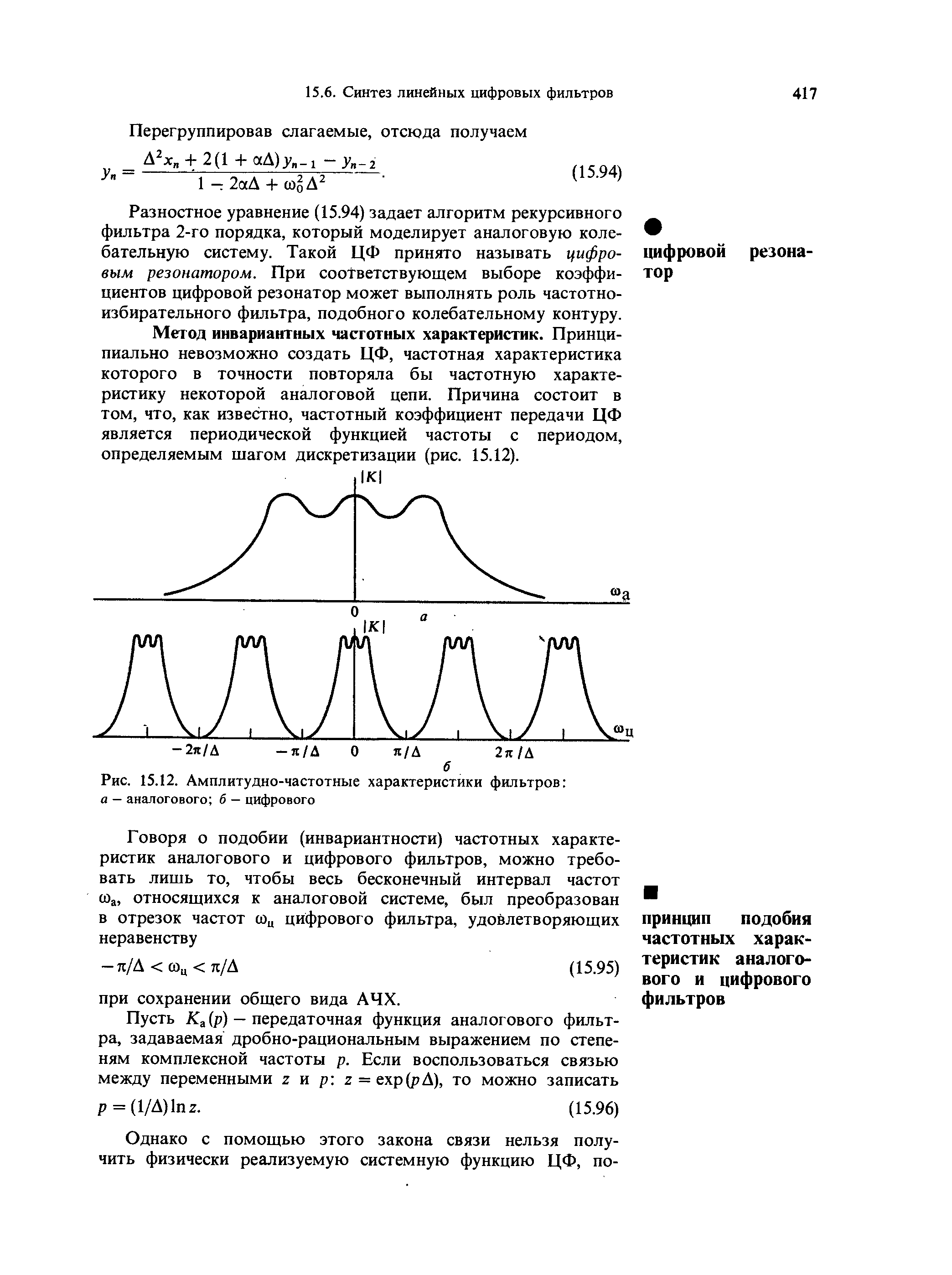 Билинейное Z – преобразование. Билинейное Z – преобразование – это специальная установка, которая позволяет получить однозначное соответствие между точками в z – плоскости со всеми точками мнимой области в р – плоскости. В справочниках: 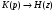 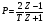 - билинейное Z – преобразование. - билинейное Z – преобразование.В результате замены получается система функций цифрового фильтра. Частоты аналоговой и цифровой системы связаны следующим соотношением: 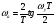 Если частота дискретизации достаточно велика 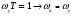 , где Т = 1/fs – интервал дискретизации. , где Т = 1/fs – интервал дискретизации.На низких частотах характеристики аналогового и цифрового фильтров практически совпадают. Рассмотрим синтез фильтра 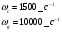 частоты среза. частоты среза.Определим шаг дискретизации: 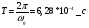 Рассчитываем частоту среза фильтра – прототипа. 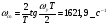 12 Находим передаточную функцию аналогового фильтра прототипа. 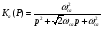 Выполним замену переменной p и находим систему функции цифрового фильтра. 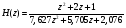 26 Вопрос. Прямые методы синтеза фильтров. Название означает, что в данном случае не используется аналоговый фильтр прототип. Исходными данными для синтеза чаще всего применяется АЧХ фильтра. Прямые методы синтеза разделяются на категории:
Перечень субоптимальных методов:
27 Вопрос. DSP (Digital Signal Processing). DSP – процессоры разделяют на 2 категории: универсальные и специализированные. Пример, DSP процессор семейства TMS320 фирмы Texas Instruments. Существуют 2 типа специализированных процессоров:
Устройства этого типа называются алгоритмическим в и DSP – процессорами.
DMA позволяет получить прямой доступ к памяти MSP430, STM32. В простейшем случае, для задач оцифровки сигналов может быть использован компьютерный процессор с Фон-неймановской архитектурой. Алгоритм цифровой обработки включает в себя повторяющиеся арифметические операции, характеризующиеся интенсивным обращением к памяти и интенсивной передачей данных через процессор. В DSP – процессоре подзадачи цифровой обработки оптимизированы и система команд, и аппаратная архитектура. Для целей оптимизации процесса применяются следующие средства:
Достоинством гарвардской архитектуры по сравнению с Фон-неймановской является то, что вызов специальной команды мажет выполняться с выполнением текущей. В большинстве DSP – процессоров применяется расширенная гарвардская архитектура, где разрешена связь между областями памяти и команд. Применяют DSP – процессоры с фиксированной запятой и плавующей. Архитектура с плавущей запятой позволяет минимизировать влияние конечной разрядности, которая проявляется как переполнение ошибки квантования и ошибки округления. Применение чисел с плавующей точкой позволяет легче переносить алгоритмы, отлаженные на ПК на языках высокого уровня. DSP – процессоры могут программироваться на языках высокого уровня или ассемблере. |
