№
|
вопрос
|
варианты ответов
|
38
?
|
Какой способ проецирования дает наиболее наглядное изображение предмета?
|
косоугольный
параллельный
перспективный
ортогональный
центральный
|
 39 39
|
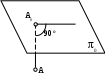
Какой способ проецирования применён при проецировании точки А на плоскость 0?
|
косоугольный
параллельный
перспективный
ортогональный
центральный
|
     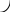
45
С
С0
0
 40 40
|
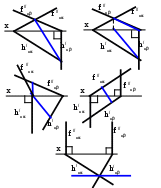
Какой способ проецирования применён при проецировании точки С на плоскость 0?
|
косоугольный
параллельный
перспективный
ортогональный
центральный
|
41
?
|
Как обозначается проекция точки А на плоскость, если проецирующая прямая параллельна этой плоскости?
|
А
А
А
А0
А
|
42
|
Какие плоскости проекций являются основой метода Монжа?
|
1
2
3
12
123
|
43
|
Какое положение в системе 1,2 должна занять новая плоскость проекций 3, вводимая для образования системы 3,1?
|
3 1
3 1
3 2
3 2
3 ох
|
№
|
вопрос
|
варианты ответов
|
44
|
Какое положение займет новая плоскость проекций 4 при определении угла наклона прямой АВ к плоскости проекций 1?
|
4 АВ
4 АВ
4 АВ
4 ох
4 ох
|
45
|
Какое положение займет новая плоскость проекций 4 при определении угла наклона прямой АВ к плоскости проекций 2?
|
4 АВ
4 АВ
4 АВ
4 ох
4 ох
|
46
|
Какое положение займет новая плоскость проекций 4 при определении расстояния между двумя параллельными плоскостями и ?
|
4 ох
4 оу
4 оz
4
4
|
47
|
Сколько новых плоскостей проекций необходимо ввести для определения угла между двумя пересекающимися плоскостями общего положения?
|
одну
две
три
ни одной
сколько угодно
|
48
|
Какое положение займет новая фронтальная плоскость проекций 4 для того, чтобы плоскость в новой системе 1,4 оказалась фронтально-проецирующей?
|
4
4 ох
4 оу
4
4 oz
|
49
|
Сколько новых плоскостей проекций необходимо ввести для определения истинной величины плоской фигуры общего положения?
|
одну
две
три
ни одной
сколько угодно
|
50
|
Какая координата точки при введении новой плоскости проекций 4 1 будет одинаковой для системы 1, 2 и 1, 4?
|
по оси Х
по оси У
по оси Z
все
ни одна
|
51
|
Какая из этих плоскостей не может быть новой плоскостью проекций?
|
горизонтально - проецирующая
фронтально - проецирующая
горизонтальная
фронтальная
общего положения
|
№
|
вопрос
|
варианты ответов
|
52
|
Сколько новых плоскостей проекций необходимо ввести для определения истинной длины отрезка прямой АВ?
|
одну
две
три
ни одной
сколько угодно
|
53
|
При использовании метода вращения, что меняет своё положение в пространстве?
|
горизонтальная плоскость проекций 1;
фронтальная плоскость проекций 2;
плоскости проекций 1, 2, 3;
объект;
объект и плоскость вращения.
|
54
|
Что такое плоскость вращения?
|
горизонтальная плоскость проекций 1;
фронтальная плоскость проекций 2;
плоскость, в которой перемещается объект вращения вокруг оси вращения;
любая горизонтальная плоскость;
любая плоскость.
|
55
|
Как плоскость вращения располагается по отношению к оси вращения?
|
перпендикулярно к оси вращения;
под любым углом к оси вращения;
независимо от оси вращения, но параллельно 1;
независимо от оси вращения, но параллельно 2;
параллельно оси вращения.
|
56
|
Где находится центр вращения точки при повороте её вокруг некоторой оси?
|
в любой точке плоскости 1;
в любой точке плоскости 2;
в точке пересечения оси вращения с плоскостью вращения;
в любой точке плоскости вращения;
в плоскости вращения по построению.
|
57
|
Основные элементы метода вращения?
|
объект вращения, ось вращения, плоскость вращения, центр вращения, радиус вращения;
ось вращения, радиус вращения, объект вращения;
объект вращения, ось вращения, плоскость вращения;
объект вращения, ось вращения, центр вращения, радиус вращения;
объект вращения, ось вращения;
|
№
|
вопрос
|
варианты ответов
|
58
|
Точка вращается вокруг оси плоскости проекций 1.
Как перемещается её горизонтальная проекция?
|
по линии ОХ;
по линии ОУ;
по окружности с произвольным центром;
по окружности, центром которой является проекция оси вращения на плоскость;
по произвольной кривой.
|
59
|
Точка вращается вокруг оси плоскости проекций 1.
Как перемещается её фронтальная проекция?
|
по линии ОХ;
по линии ОУ;
по окружности с произвольным центром;
по окружности, центром которой является проекция оси вращения на плоскость;
по произвольной кривой.
|
60
|
Точка вращается вокруг оси плоскости проекций 2.
Как перемещается её горизонтальная проекция?
|
по линии ОХ;
по линии ОУ;
по окружности с произвольным центром;
по окружности, центром которой является проекция оси вращения на плоскость;
по произвольной кривой.
|
61
|
Точка вращается вокруг оси плоскости проекций 2.
Как перемещается её фронтальная проекция?
|
по линии ОХ;
по линии ОУ;
по окружности с произвольным центром;
по окружности, центром которой является проекция оси вращения на плоскость;
по произвольной кривой.
|
62
|
Как перемещается точка прямой, лежащая на оси вращения, плоскости проекций 1?
|
по линии ОХ;
по линии ОУ;
по окружности;
не меняет своего положения;
но произвольной кривой.
|
63
|
Прямая АВ повёрнута вокруг оси, плоскости 1, на угол .
На какой угол будут повёрнуты горизонтальные проекции точек А и В?
|
на угол А и угол В;
на угол А;
на угол В;
на угол угла ;
на угол .
|
64
|
Вокруг какой оси надо повернуть прямую АВ, чтобы получить её истинную величину во фронтальной плоскости проекций 2?
|
оси, плоскости 1;
оси, плоскости 2;
оси, плоскости 1;
оси, плоскости 1 и 3;
произвольной оси.
|
№
|
вопрос
|
варианты ответов
|
65
|
Вокруг какой оси надо повернуть прямую АВ, чтобы получить её истинную величину во фронтальной плоскости проекций 2?
|
оси, плоскости 1;
оси, плоскости 2;
оси, плоскости 1;
оси, плоскости 1 и 3;
ороизвольной оси.
|
66
|
Какая из проекций отрезка прямой линии при вращении вокруг оси, плоскости 1, не изменяет своей величины?
|
фронтальная проекция;
горизонтальная проекция;
профильная проекция;
фронтальная и горизонтальная проекции;
все проекции меняют свою величину.
|
67
|
Как называется метод вращения, при котором оси вращения, плоскости 1 и плоскости 2 не указываются, а проекции точек допускается перемещать в плоскостях их вращения на свободное поле чертежа?
|
метод свободного вращения;
метод плоскопараллельного перемещения;
метод совмещения;
метод вращения и перемещения;
комбинированный метод вращения.
|
68
|
Вокруг какой оси надо повернуть плоскость треугольника, чтобы его плоскость стала фронтально проецирующей?
|
вокруг оси, плоскости 1;
вокруг оси, плоскости 2;
вокруг оси, плоскости 1;
вокруг осей, плоскости 1 и 2;
вокруг любой оси.
|
69
|
В каком случае не изменяется при вращении наклон прямой линии по отношению к плоскости 3?
|
вокруг оси, плоскости 1;
вокруг оси, плоскости 2;
вокруг оси, плоскости 3;
вокруг оси, плоскости 1;
вокруг любой оси.
|
70
|
Путём поворота вокруг какой оси можно определить длину отрезка прямой линии и угол её наклона к плоскости 1?
|
поворотом вокруг оси, пл. 1;
поворотом вокруг оси, пл. 2;
поворотом вокруг оси, пл. 3;
поворотом вокруг оси, пл. 1;
поворотом вокруг оси, пл. 2;
|
71
|
Вращением, вокруг какой оси можно получить истинную величину плоской фигуры общего положения?
|
вокруг оси, плоскости 1;
вокруг оси, плоскости 2;
вокруг оси, плоскости 1;
вокруг горизонтали плоской фигуры;
вокруг любой оси, пл. 2.
|
№
|
вопрос
|
варианты ответов
|
72
|
Какому методу присуще совмещение заданной плоскости и расположенных в ней геометрических элементов с соответствую- щими плоскостями проекций?
|
методу вращения вокруг оси, плоскости проекций;
методу вращения вокруг оси, плоскости проекций;
методу вращения вокруг следа заданной плоскости;
методу плоскопараллельного перемещения;
вращению вокруг любой оси.
|
73
|
Как называется метод вращения вокруг следа заданной плоскости?
|
метод вращения вокруг оси, плоскости проекций;
метод вращения вокруг горизонтали;
метод вращения вокруг фронтали;
метод совмещения;
метод плоскопараллельного перемещения.
|
74
|
Какие элементы должны быть заданы для определения истинной величины фигуры, лежащей в плоскости, с помощью метода совмещения?
|
следы плоскости и две проекции фигуры;
один из следов плоскости и одна проекция фигуры;
два следа плоскости и одна проекция фигуры;
все следы плоскости и точка привязки фигуры;
два следа плоскости и точка привязки фигуры.
|
75
|
Какие элементы должны быть заданы для построения проекций фигуры, лежащей в плоскости, с помощью метода совмещения?
|
следы плоскости и истинная величина фигуры;
два следа плоскости, истинная величина фигуры и точка привязки фигуры к плоскости;
два следа плоскости и истинная величина фигуры;
три следа плоскости и истинная величина фигуры;
след плоскости, ось вращения, истинная величина фигуры и одна проекция точки привязки фигуры к плоскости.
|
№
|
вопрос
|
варианты ответов
|
76
|
Плоский угол проецируется на горизонтальную плоскость проекции 1 без искажения, если:
|
плоский угол является плоскостью общего положения;
плоский угол является горизонтально – проецирующей плоскостью;
плоский угол горизонтальной плоскости проекций 1;
плоский угол фронтальной плоскости проекций 2;
плоский угол является фронтально – проецирующей плоскостью;
|
77
|
Какие плоские углы, являющиеся плоскостями общего положения, проецируются на плоскости проекций без искажения?
|
если плоскость угла является горизонтально – проецирующей плоскостью;
если плоскость угла является фронтально – проецирующей плоскостью;
если плоскость угла является любой проецирующей плоскостью;
прямой угол, катет которого параллелен плоскости проекций;
никакие.
|
78
|
Когда прямой угол, плоскость которого является плоскостью общего положения, проецируется на плоскость проекций без искажения?
|
всегда;
если один из катетов параллелен плоскости проекций;
всегда с искажением;
если плоскость угла плоскости проекций 1;
если плоскость угла плоскости проекций 2;
|
№
|
вопрос
|
варианты ответов
|
 79 79
|
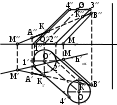
Положение вспомогательной секущей плоскости относительно плоскостей проекций.
|
горизонтально – проецирующая плоскость;
плоскость общего положения, проходящая через ось цилиндра;
фронтально – проецирующая плоскость;
плоскость общего положения, параллельная оси цилиндра;
осевая плоскость.
|
 80 80
|
Какая фигура получается в результате пересечения вспомогательной секущей плоскости с поверхностью цилиндра?
|
окружность;
треугольник;
эллипс;
четырёхугольник;
трапеция.
|
 81 81
|
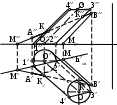
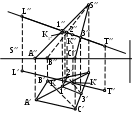
С какими гранями пирамиды пересекается прямая LT?
|
SCA и SAB;
ABC и SCA;
SCB и ABC;
SCB и SCA;
SCB и SAB.
|
 82 82
|
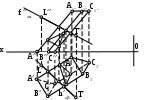
Положение прямой LT относительно геометрического тела АВСС1В1А1.
|
пересекает грани АВВ1А1 и АСС1А1;
пересекает грани ВСС1В1 и АВВ1А1;
пересекает грани АВС и А1В1С1;
не пересекает поверхность призмы;
пересекает грани ВСС1В1 и АСС1А1.
|
№
|
вопрос
|
варианты ответов
|
0
 83 83
|
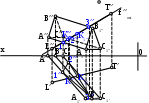
Показать правильно видимость прямой LT относительно поверхности призмы на фронтальной проекции.
|
невидимая на всём протяжении от точки 1” до точки 3”;
невидима на участке К”К1”;
видимая на всём протяжении от точки 1” до точки 3”;
видима от точки 1” до точки К”, невидима от точки К” до точки 3”;
видима от точки К1”до точки 3”, невидима от точки 1” до точки К1” .
|
x
84
|
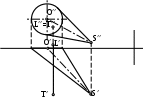
Если прямая LT пересекает поверхность конуса, то каким образом?
|
пересекает боковую поверхность конуса;
пересекает только основание конуса;
не пересекает поверхность конуса;
пересекает ближнюю к зрителю полуповерхность конуса и его основание;
пересекает дальнюю от зрителя полуповерхность конуса и его основание.
|
D
A
B
A
D
C
ho
x

C
B
                      
1
2
3
4
6
5

S
A
L
T
1
2
3
4
5
6

A
T
L
0
85
|
Назвать горизонтальные проекции точек пересечения прямой LT с поверхностью пирамиды.
|
1 и 6;
3 и 4;
4 и 5;
2 и 5;
3 и 5.
|
   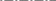         
О1
О
О1
О
fo
х
hо
 86 86
|
Какие вспомогательные секущие плоскости следует использовать в данном варианте для нахождения линии пересечения цилиндрической поверхности плоскостью ?
|
фронтально проецирующие плоскости;
плоскости общего положения;
профильно проецирующие плоскости;
горизонтально проецирующие плоскости;
осевые плоскости.
|
№
|
вопрос
|
варианты ответов
|
            
О1
О
О1
О
fo
х
hо
х
87
|
Какая фигура получается в результате пересечения плоскости с поверхностью цилиндра?
|
окружность;
эллипс;
параллелограмм;
квадрат;
прямоугольник.
|
х
88
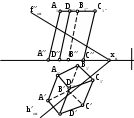
|
Какие боковые ребра призмы пересекают плоскость ?
|
AA1 и DD1;
CC1и DD1;
BB1 и CC1;
AA1 и BB1;
AA1 и СС1.
|
 89 89
|
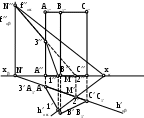
Какие грани призмы пересекает плоскость ?
|
грани АСС1А1 и СВВ1С1;
грани АВВ1А1 и СВВ1С1;
грани АВС и А1В1С1;
грани АВВ1А1 и АСС1А1;
грани АВС, АВВ1А1 и АСС1А1.
|
№
|
вопрос
|
варианты ответов
|
х
0
90
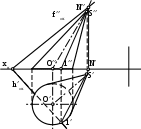
|
Какая фигура получается в результате пересечения плоскости с поверхностью конуса?
|
эллипс;
окружность;
треугольник;
парабола;
гипербола.
|
              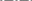
         
О1
2
1
О
1
М
О1
О
М
2
ho
fo

x
х
0
91
|
Какая фигура получается в результате пересечения плоскости с поверхностью цилиндра?
|
окружность;
эллипс;
прямоугольник;
парабола;
параллелограмм.
|
 92 92
|
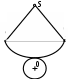
Развёртка полной поверхности какого геометрического тела изображена на рисунке?
|
наклонного конуса;
правильной пирамиды;
прямого конуса;
наклонного цилиндра;
прямого цилиндра.
|
№
|
вопрос
|
варианты ответов
|
 93 93
|
По какой формуле определяется угол при построении развёртки боковой поверхности прямого конуса?
|
= 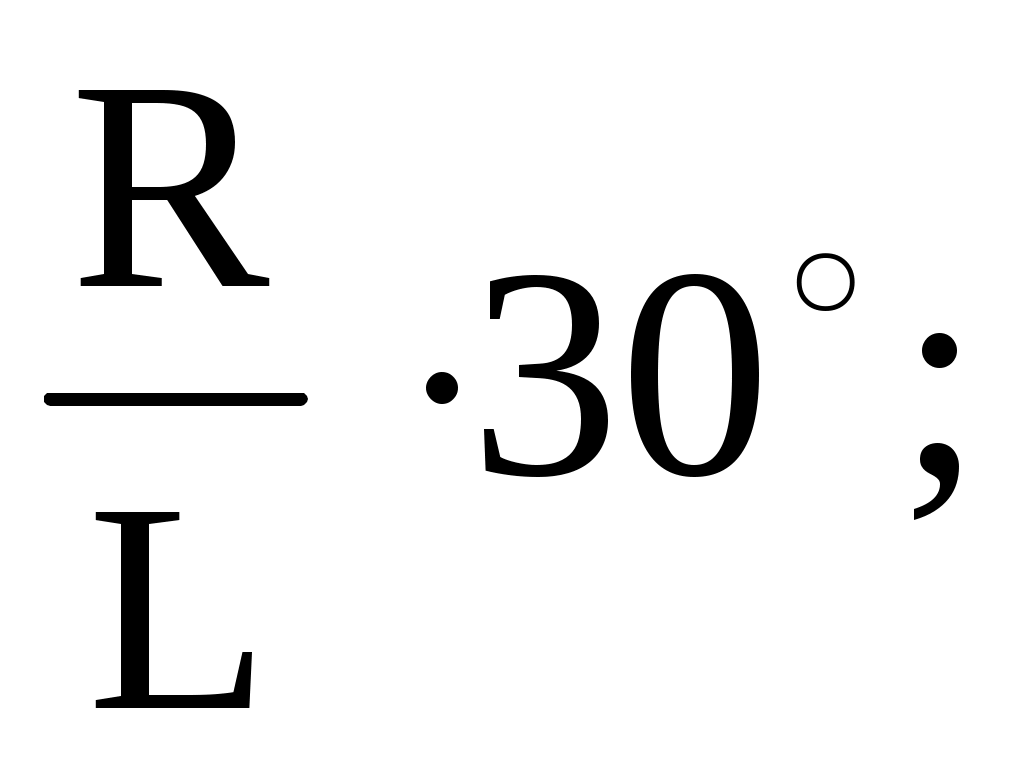
= 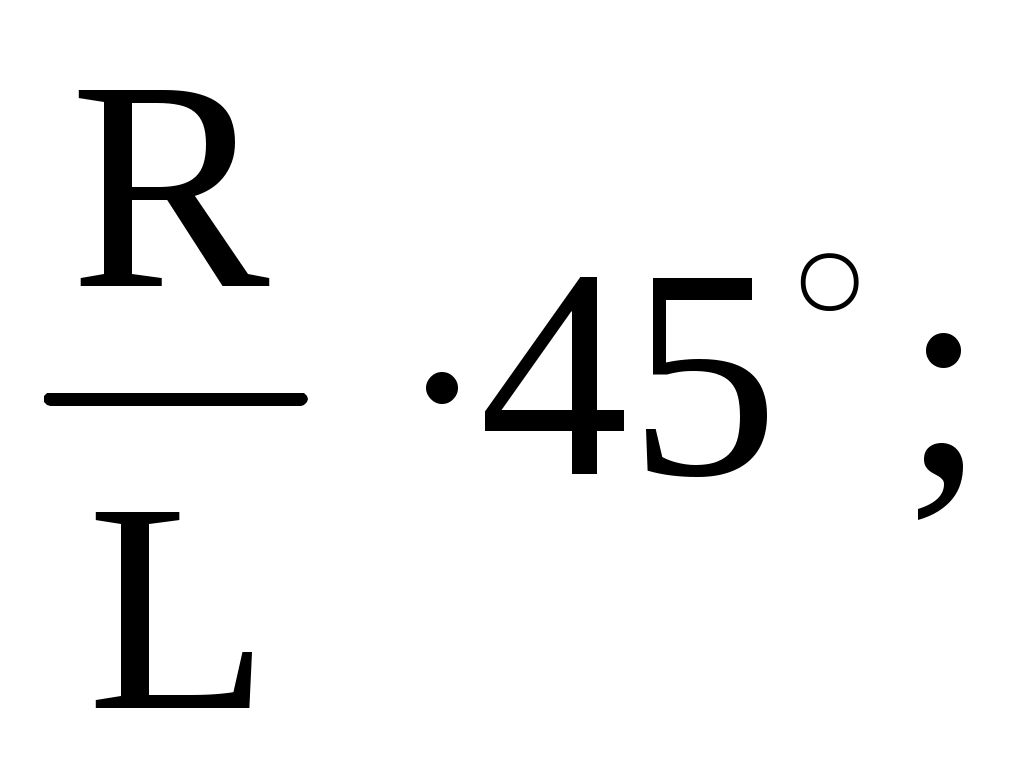
= 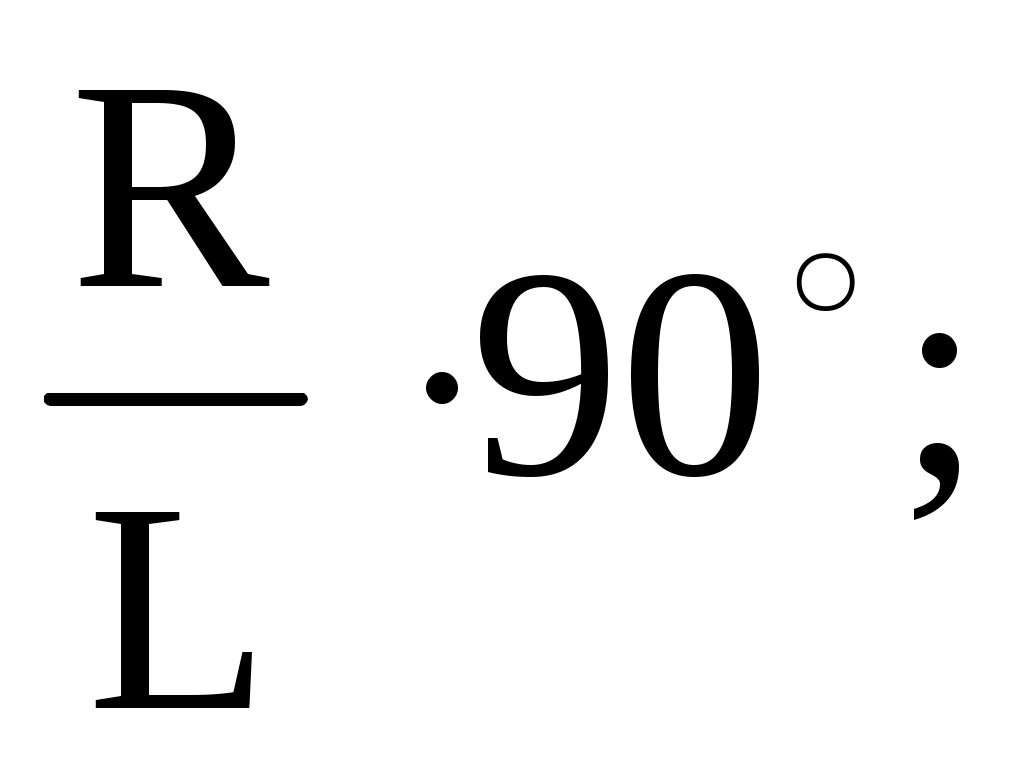
= 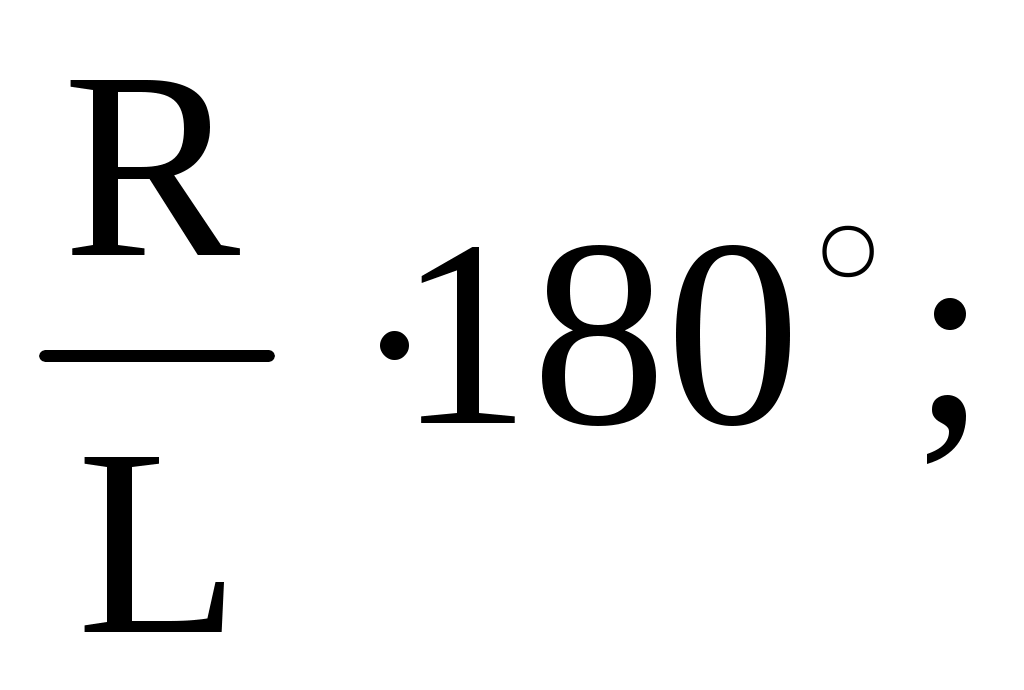
= 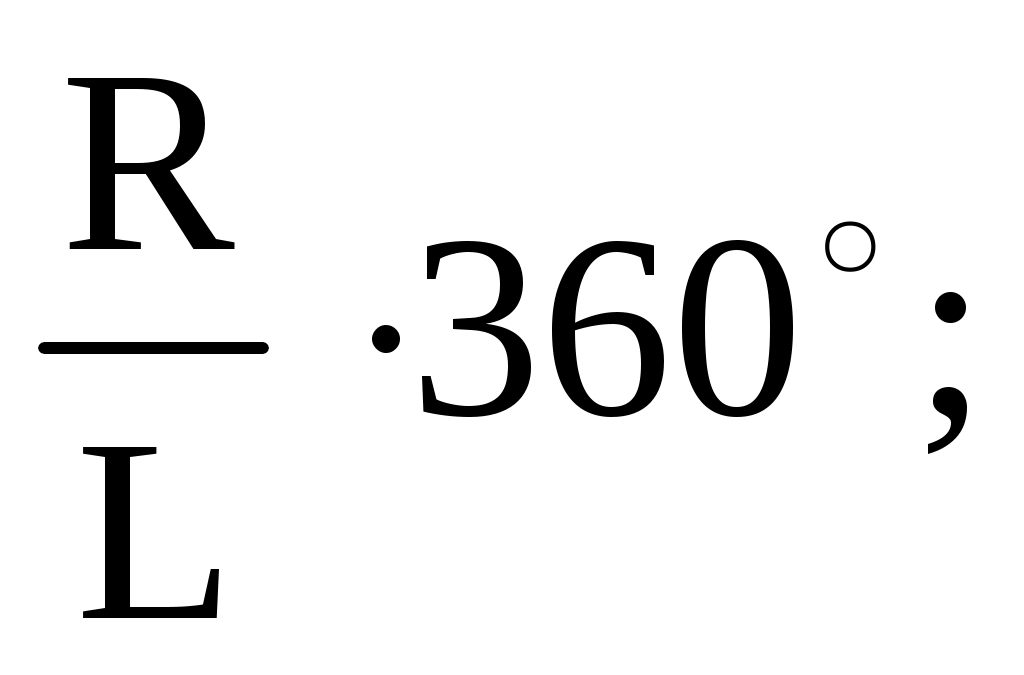
где R – радиус основания конуса?
L – длина образующих конуса.
|
94
|
Каким способом определяется истинная длина образующих прямого конуса при построении его развёртки?
|
способом прямоугольного треугольника;
способом вращения;
способом перемены плоскостей проекций;
способом плоско–параллельного перемещения;
определять не надо.
|
95
|
Какой способ следует применять при определении истинной длины рёбер наклонной пирамиды при построении её развёртки?
|
способом прямоугольного треугольника;
способом вращения;
способом перемены плоскостей проекций;
способом плоско–параллельного перемещения;
никакой.
|
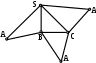 96 96
|
Развёртка полной поверхности какого геометрического тела изображена на рисунке?
|
конуса;
цилиндра;
наклонной призмы;
наклонной пирамиды;
прямой пирамиды.
|
97
|
Какой способ надо применить при определении истинной длины рёбер прямой призмы при построении её развёртки?
|
способом прямоугольного треугольника;
способом вращения;
способом перемены плоскостей проекций;
способом плоско–параллельного перемещения;
никакой.
|
№
|
вопрос
|
варианты ответов
|
98
|
Какой способ надо применить при определении истинной длины рёбер наклонной призмы при построении её развёртки?
|
способом прямоугольного треугольника;
способом вращения;
способом перемены плоскостей проекций;
способом плоско–параллельного перемещения;
никакой.
|
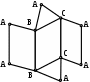 99 99
|
Развёртка полной поверхности какого геометрического тела изображена на рисунке?
|
прямой призмы;
наклонной призмы;
прямого цилиндра;
наклонного цилиндра;
прямого конуса.
|
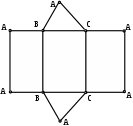 100 100
|
Развёртка полной поверхности какого геометрического тела изображена на рисунке?
|
прямой призмы;
наклонной призмы;
прямого цилиндра;
наклонного цилиндра;
прямого конуса.
|
Заведующий каф. НГ и Г проф. Бобин Н. Е.
Составители:
проф. Онищин В. П.
доц. Эйст Ю. А.
доц. Мураев Ю. Д.
доц. Пашкевич В. М.
доц. Галушкин С. С.
асс. Игнатьев С. А.
|
 Скачать 0.53 Mb.
Скачать 0.53 Mb.