1.
|
Дайте определение понятия «вращательное движение».
Ответ: Вращательное движение – это движение всех точек тела, находящихся в плоскостях, перпендикулярных неподвижной прямой, называемой осью вращения, и описывание окружностей, центры которых располагаются на этой оси.
|
2.
|
Дайте определение угловой координаты.
Ответ: Угловая координата - любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается r) соответствует расстоянию от точки до начала координат. Угловая координата, также называется полярным углом или азимутом и обозначается arphi, равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.
Угловой координатой называется угол phi между положительным направлением оси X и проекцией радиуса - вектора r некоторой точки тела на координатную плоскость XY.
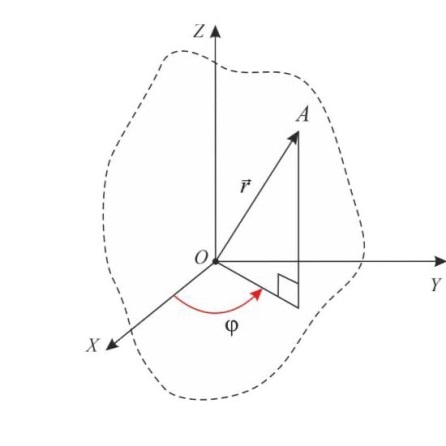
|
3.
|
Дайте определение вектора углового перемещения. Как определяется его направление?
Ответ:Вектор углового перемещения -это вектор, определяющий, как вращается твердое тело.
Направление вектора определяется правилом правого винта: если головку винта вращать в направлении вращении тела, то направление поступательного движения винта совпадает с направлением вектора.
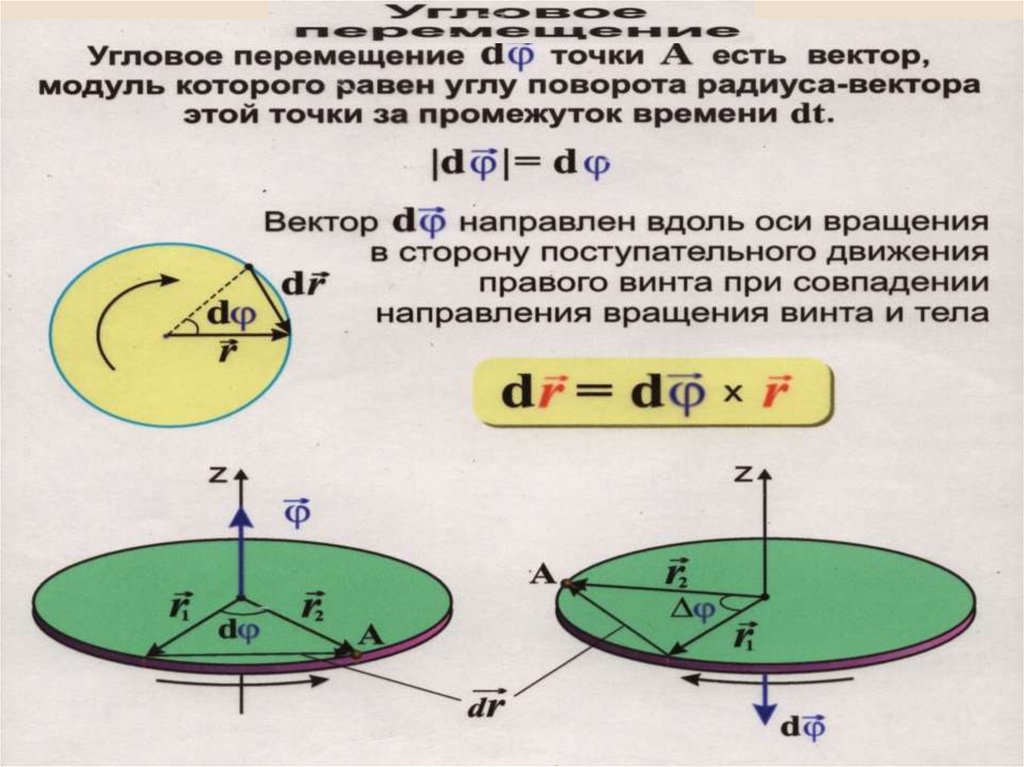

|
4.
|
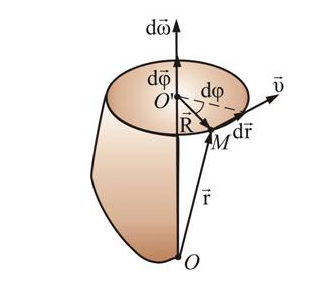
Дайте определение вектора угловой скорости. Как определяется его направление?
Ответ: Угловой скоростью называется вектор 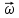 , численно равный первой производной от угла поворота по времени и направленный вдоль оси вращения в направлении d , численно равный первой производной от угла поворота по времени и направленный вдоль оси вращения в направлении d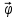 ( (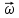 и d и d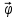 всегда направлены в одну сторону). всегда направлены в одну сторону). 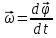 Если ω = const, то имеет место равномерное вращение тела вокруг неподвижной оси. Если ω = const, то имеет место равномерное вращение тела вокруг неподвижной оси.
|
5.
|
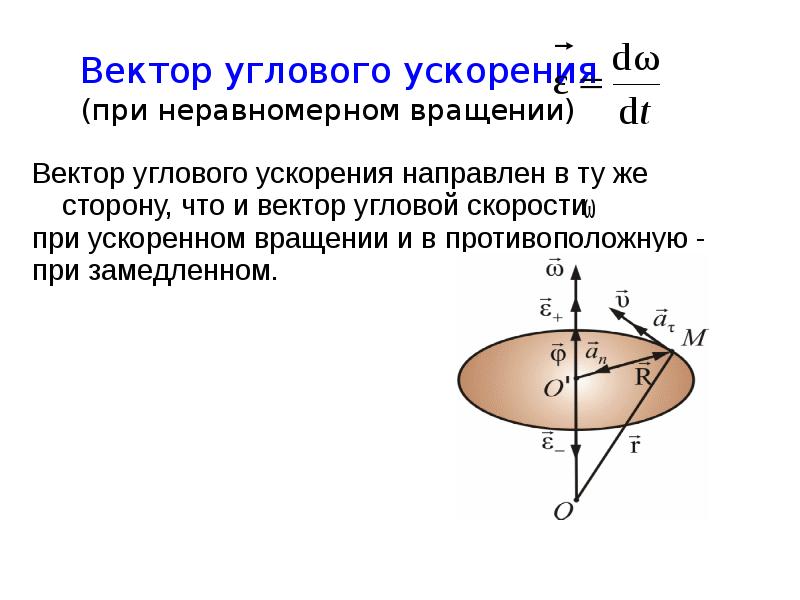
Дайте определение вектора углового ускорения. Как определяется его направление?
Ответ:
Вектор углового ускорения – это вектор численно равный первой производной по времени от закона изменения угловой скорости направленный по оси вращения
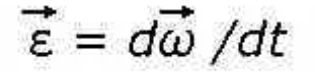
|
6.
|
Дайте определение момента инерции (как рассчитывается и каков его физический смысл?)
Ответ: Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр. Момент инерции равен произведению массы материальной точки на квадрат расстояния др оси вращения. Это аналог массы во вращательном движении.
Общая формула
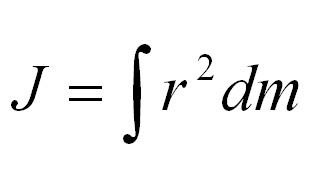
Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:
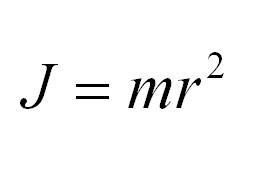 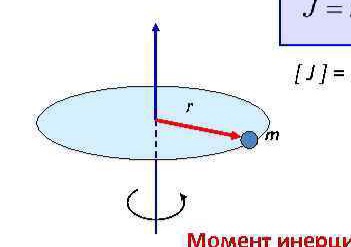
|
7.
|
Дайте определение вектора момента импульса относительно точки, момента импульса относительно оси. Укажите направление вектора момента импульса.
Ответ: Момент импульса относительно точки. Это векторная величина равная произведению радиус-вектора r и вектора импульса P.
Момент импульса относительно оси. Это скалярная величина равная проекции момента импульса относительно точки О на ось z проходящую через эту точку.
Направление вектора момента импульса определяется по правилу правого винта
|
8.
|
Дайте определение вектора момента силы относительно точки, момент силы относительно оси. Укажите направление вектора момента силы.
Ответ: Момент силы относительно точки О. Это векторная величина равная произведению радиус вектора (соединяющего точку О и точку приложения силы ) и силы.
Момент силы относительно оси. Это проекция момента силы относительно точки О на ось z проходящую через эту точку.
Направление по правила правого винта при вращ. в сторону наим-го угла.
|
9.
|
Назовите единицу измерения угловой скорости в системе СИ.
Ответ: Единицы измерения в системе в СИ - рад/с.
|
10.
|
Назовите единицу измерения углового ускорения в системе СИ.
Ответ: Единица измерения углового ускорения - рад/с2.
|
11.
|
Назовите единицу измерения момента импульса в системе СИ.
Ответ: Размерность момента импульса в системе СИ : кг•м2 /с
|
12.
|
Назовите единицу измерения момента силы в системе СИ.
Ответ: Момент силы имеет размерность «сила, умноженная на расстояние» и единицу измерения ньютон-метр (джоуль) в системе СИ. 1 Н·м — это момент, который производит сила 1 Н на рычаг длиной 1 м, приложенная к концу рычага и направленная перпендикулярно ему.
|
13.
|
Назовите единицу измерения момента инерции в системе СИ.
Ответ: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Единица измерения в Международной системе единиц (СИ): кг·м². Обозначение: I или J.
|
14.
|
Как связаны линейные и угловые кинематические характеристики при вращательном движении?
Ответ: 
|
15.
|
Как рассчитывается работа сил при вращательном движении?
Ответ: 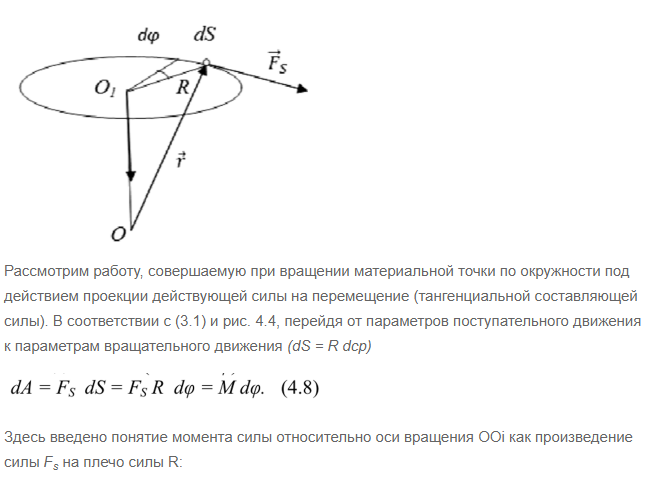

|
16.
|
Как рассчитывается кинетическая энергия тела, вращающегося вокруг неподвижной оси?
Ответ: 
|
17.
|
Как связаны кинетическая энергия тела и работа сил при вращательном движении?
Ответ: Работа внешних сил при вращении тела идет на увеличение его кинетической энергии.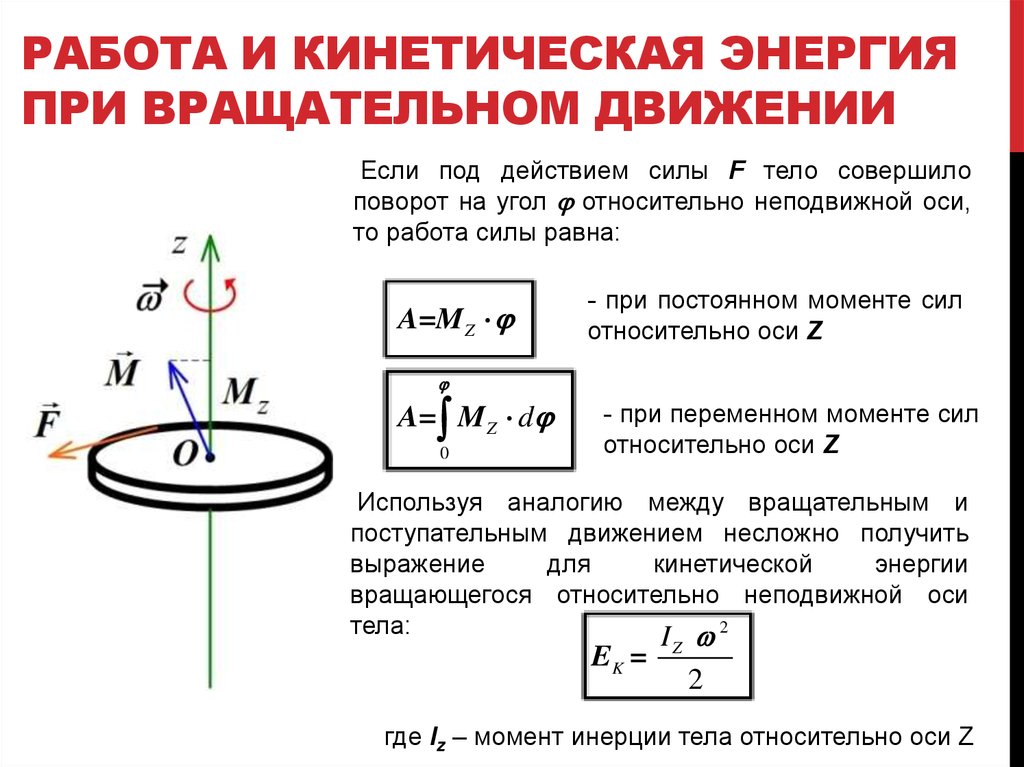
|
18.
|
Как связаны вектор момента импульса и вектор момента силы при вращательном движении тела?
Ответ:
|
19.
|
Сформулируйте теорему Штейнера.
Ответ: Теорема Штейнера: момент инерции тела относительно произвольной оси равен инерции тела относительно параллельной оси, проходящей через центр масс тела, плюс произведение массы тела на квадрат расстояния между осями.

|
20.
|
Сформулируйте основной закон динамики вращательного движения.
Ответ: Основной закон динамики вращательного движения
Производная по времени от момента количества движения механической системы относительно неподвижной инерциальной системы отсчёта точки или центра инерции системы равна главному моменту относительно той же точки всех внешних сил, приложенных к системе.
И ЛИ: ЛИ:

|
21.
|
Сформулируйте закон сохранения момента импульса для системы тел.
Ответ: Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени.
Закон сохранения импульса выполняется и в том случае, если на тела системы действуют внешние силы, векторная сумма которых равна нулю.
Математически закон сохранения момента импульса выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел, которая остается постоянной, пока на систему не воздействуют моменты внешних сил. В соответствии с этим момент импульса замкнутой системы в любой системе координат не изменяется со временем.
Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота.
Если механическая система находится в равновесии, то закон сохранения момента импульса записывается в виде
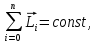
Где 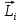 момент импульса момент импульса 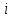 – той частицы, а суммирование производится по всем частицам замкнутой механической системы. – той частицы, а суммирование производится по всем частицам замкнутой механической системы.
|
 Скачать 1.02 Mb.
Скачать 1.02 Mb.


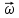 , численно равный первой производной от угла поворота по времени и направленный вдоль оси вращения в направлении d
, численно равный первой производной от угла поворота по времени и направленный вдоль оси вращения в направлении d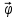 (
(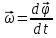 Если
Если 

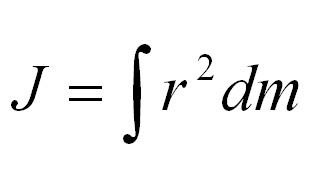
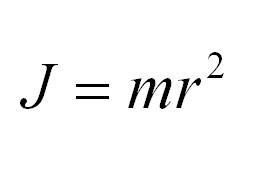







 ЛИ:
ЛИ: 
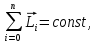
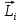 момент импульса
момент импульса 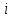 – той частицы, а суммирование производится по всем частицам замкнутой механической системы.
– той частицы, а суммирование производится по всем частицам замкнутой механической системы.