Ответы на вопросы к экзамену. Вопросы к экзамену Как определить взаимные проводимости (расчетным и экспериментальным путем)
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
Катушка индуктивности — винтовая, спиральная или винтоспиральная катушка из свёрнутого изолированного проводника, обладающая значительной индуктивностью при относительно малой ёмкости и малом активном сопротивлении. Как следствие, при протекании через катушку переменного электрического тока, наблюдается её значительная инерционность. Применяются для подавления помех, сглаживания пульсаций, накопления энергии, ограничения переменного тока, в резонансных(колебательный контур) и частотноизбирательных цепях, в качестве элементов индуктивности искусственных линий задержки с сосредоточенными параметрами, создания магнитных полей, датчиков перемещений и так далее. Основным параметром катушки индуктивности является её индуктивность, численно равная отношению создаваемого током потока магнитного поля, пронизывающего катушку к силе протекающего тока. Типичные значения индуктивностей катушек от десятых долей мкГн до десятков Гн. Индуктивность катушки пропорциональна линейным размерам катушки, магнитной проницаемости сердечника и квадрату числа витков намотки. Индуктивность катушки-соленоида[источник не указан 265 дней]: где — магнитная постоянная, — относительная магнитная проницаемость материала сердечника (зависит от частоты), — площадь сечения сердечника, — длина средней линии сердечника, — число витков. 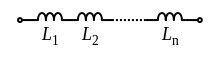 Схема последовательного соединения катушек индуктивности. Ток через каждую катушку один и тот же. При последовательном соединении катушек общая индуктивность равна сумме индуктивностей всех соединённых катушек: 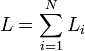 . .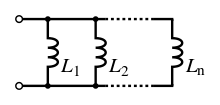 Электрическая схема параллельного соединения нескольких катушек индуктивности. Напряжение на всех катушках одинаково При параллельном соединении катушек общая индуктивность равна: 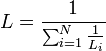 . .32. Сформулируйте законы коммутации 14.2. Законы (правила) коммутации Согласно первому закону коммутации, ток через индуктивность не может измениться скачком, т.е. ток через индуктивность до коммутации равен току через индуктивность после коммутации: iL(0-)=iL(0+). Доказать это можно, рассматривая уравнение (14.1). Если бы ток мог измениться скачком, то 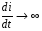 , и левая часть уравнения не будет равна правой. , и левая часть уравнения не будет равна правой.Иногда приходится использовать более общий закон – закон сохранения потокосцеплений: сумма потокосцеплений до коммутации равна сумме потокосцеплений после коммутации 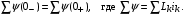 Согласно второму закону коммутации, напряжение на емкости не может измениться скачком, т.е. напряжение на емкости до коммутации равно напряжению на емкости после коммутации: uc(0-)=uc(0+). Доказывается это аналогично предыдущему. Если бы была возможность изменения напряжения на конденсаторе скачком, то 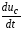 стремилась бы к бесконечности и в уравнении цепи, содержащей сопротивление и конденсатор, стремилась бы к бесконечности и в уравнении цепи, содержащей сопротивление и конденсатор, 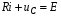 или или 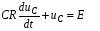 (так как (так как 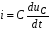 ) левая часть не была бы равна правой. ) левая часть не была бы равна правой. Иногда приходится использовать более общий закон сохранения заряда: заряд в цепи до коммутации равен заряду в цепи после коммутации 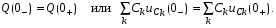 33. Нарисовать график тока i=10(e-100t – e-400t) 34. Нарисовать график u= 1000e-100tsin500t 35. Нарисовать график тока в цепи RLC при подключении под постоянное напряжение, если корни характеристического уравнения вещественные. 36. Нарисовать график напряжения на индуктивном элементе UL в цепи RLC при подключении под постоянное напряжение, если корни характеристического уравнения вещественные. 37. Нарисовать график тока в цепи RLC при подключении под постоянное напряжение, если корни характеристического уравнения комплексные. 38. Нарисовать график напряжения на индуктивном элементе UL в цепи RLC при подключении под постоянное напряжение, если корни характеристического уравнения комплексные. 39. Нарисовать график напряжения на конденсаторе UС в цепи RLC при подключении под постоянное напряжение, если корни характеристического уравнения комплексные. 40. Что такое переходные и импульсные характеристики цепи? Переходные характеристики цепи h(t) определяют реакцию цепи на единичное ступенчатое возмущение. Единичной функцией 1(t) называют функцию, равную единице при t > 0 и равную 0 при t < 0. Еще одной важной функцией является единичный импульс δ(t) или дельта-функция, под которыми понимают короткий импульс амплитудой 1/Δτ, длительностью Δτ →0, действующий от t = – Δτ/2 до t = Δτ/2. Единичным его называют потому, что площадь импульса равна единице. Единицей измерения δ-функции является секунда в минус первой степени. Если импульс действует при некотором времени t = t1, то он обозначается как δ(t– t1) т.е. импульс действует, когда аргумент δ-функции равен нулю. Реакция цепи на δ-импульс называется импульсной характеристикой цепи. В общем случае величину 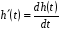 называют импульсной переходной функцией четырехполюсника называют импульсной переходной функцией четырехполюсникаПереходные и импульсные характеристики объединяются более общим понятием «временные характеристики» (в отличие от операторных). Подчеркнем, что в литературе по переходным процессам в зависимости от рассматриваемого вопроса под одним и тем же названием – импульсная переходная функция – понимают функцию либо h'(t), либо hδ(t). Между этими функциями имеется зависимость hδ(t)= h(0+) δ(t)+h'(t); При этомh'(t)характеризует реакцию четырехполюсника (его выходное напряжение) после окончания воздействия на его вход единичным импульсом напряжения 1∙ δ (t) В∙с, a hδ(t) –напряжение на выходе четырехполюсника и во время действия импульса, и после окончания. Определение h(t) и hδ(t) через К(р). Как упоминалось, при воздействии на вход четырехполюсника единичного напряжения u1(t) = 1(t) напряжение на выходе его u2(t) = h(t). Если это положение записать относительно изображений, учитывая, что 1(t)↔1/p и обозначив изображение h(t) через Н(р), то Н(р)= К(р)/р. Отсюда К(р) = р H(р). Определим теперь h(t) через К(р). Так как h(t) ↔ H(p), а Н(р) определено предыдущей строкой, то 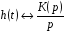 При воздействии на вход четырехполюсника единичным импульсом напряжения u1(t)=1 δ(t)=∙1 ↔U1(p),напряжение на его выходе u2(t)=hδ(t)U1(p)K(p)=∙1∙K(p). Таким образом, hδ(t)↔ K(p), т.е. – импульсная переходная функция может быть определена через оригинал операторной передаточной функции. 41. Что такое передаточная функция цепи и как ее найти? Под передаточной функциейчетырехполюсника К(р) на комплексной частоте понимают отношение выходного напряжения U2(p) ко входному U1(p) 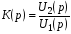 . .Если несколько четырехполюсников, например три, соединены каскадно и известны передаточные функции каждого четырехполюсника, то передаточная функция каскада равна произведению передаточных функций этих четырехполюсников: К(р)= К1(р) К2(р) К3(р). Для перехода от операторной характеристики цепи к ее комплексной частотной характеристики достаточно в уравнениях заменить p на jω. Как и комплексные частотные характеристики, операторные характеристики делятся на входные и передаточные. 42. Как связаны переходные и импульсные характеристики с передаточной функцией цепи? См.43 43. Как строится вольт-амперная характеристика двух нелинейных элементов, включенных последовательно, параллельно, при смешанном соединении нескольких нелинейных элементов. Вольт-ампе́рная характери́стика (ВАХ) — зависимость тока через двухполюсник от напряжения на этом двухполюснике. Описывает поведение двухполюсника на постоянном токе. А также функция выражающая (описывающая) эту зависимость. А также — график этой функции. Чаще всего рассматривают ВАХ нелинейных элементов (степень нелинейности определяется коэффициентом нелинейности Характерные примеры элементов, обладающих существенно нелинейной ВАХ: диод, тиристор, стабилитрон. Для трёхполюсных элементов (таких, как транзистор, тиристор или ламповый триод) часто строят семейства кривых, являющимися ВАХ для двухполюсника при так или иначе заданных параметрах на третьем выводе элемента. Необходимо отметить, что в реальной схеме, особенно работающей с относительно высокими частотами (близкими к границам рабочего частотного диапазона) для данного устройства реальная зависимость напряжения от времени может пробегать по траекториям, весьма далёким от «идеальной» ВАХ. Чаще всего это связано с ёмкостью или другими инерционными свойствами элемента. Рассмотрим несколько примеров нелинейных элементов с симметричными характеристиками: а) лампа накаливания С ростом тока сопротивление нити увеличивается и возрастание тока замедляется (рис.6). Сопротивление не зависит от направления тока. 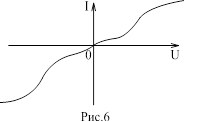  б) терморезистор С ростом тока сопротивление нити уменьшается (рис.7). Терморезистор применяют для компенсации изменений сопротивлений элементов, изготовленных из металлических проводников, сопротивление которых увеличивается с увеличением тока в цепи. При последовательном же включении общее сопротивление цепи не изменяется. 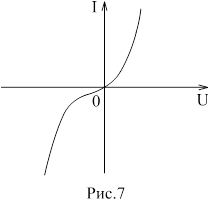 в) тиритовые и вилитовые элементы С увеличением напряжения их проводимость увеличивается. Например: при увеличении напряжения в 2 раза ток I увеличивается в 10 раз (рис.8). Из тиритовых дисков выполняют разрядники, предназначенные для защиты установок высокого напряжения от перенапряжений. 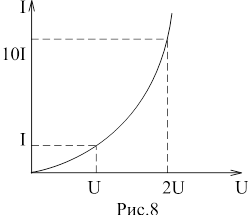 К нелинейным элементам с несимметричной вольт-амперной характеристикой относятся электронные лампы, полупроводниковые диоды, транзисторы, электрическая дуга при неоднородных электродах и прочие. Примеры: а) полупроводниковый диод Проводит электрический ток, если к аноду приложен положительный потенциал, а к катоду - отрицательный (рис.9). 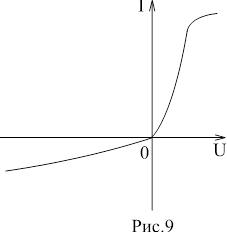  б) транзистор Ток коллектора различен для разных токов базы (рис.10) 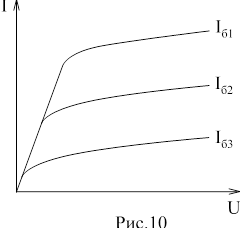 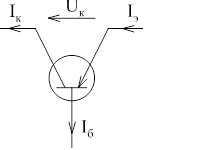 Нелинейные элементы характеризуются двумя параметрами: статическим Rст и дифференциальным Rдиф сопротивлениями. Эти сопротивления изменяются от точки к точке вольт-амперной характеристики. Статическим сопротивлением называется отношение напряжения к току в данной точке (рис.11)
44. Как определить дифференциальное сопротивление по известной ВАХ. Дифференциальное сопротивление определяется производной к ВАХ в точке А, т.е. тангенсом угла наклона касательной в точке А. 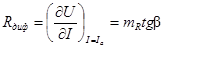 45. Можно ли получить резонансный режим в цепях с ферромагнитными элементами, изменяя только напряжение питания? Феррит, помещенный в постоянное магнитное поле Нд и перпендикулярное к нему переменное СВЧ-маг-нитное поле, поглощает СВЧ-энергию. Это поглощение носит резонансный характер (ферромагнитный резонанс) и максимально на частоте со о, определенным образом связанной с полем Но- Зависимость резонансной частотыО) о от Я о имеет сложный характер и определяется магнитнойкристаллографической анизотропией, анизотропией формы, упругонапряженным состоянием образца и т. п. [3]. В наиболее простом случае изотропной сферы [c.563]
В первых работах по магнитному резонансу в парамагнитных, ферромагнитных и антиферромагнитных веществах применяли уравнения Блоха (668), которые можно переписать так [c.381] Ферромагнитный резонанс. Сборник статей. М., Физматгиз, 1961. [c.538] Поэтому в данной части результаты теории Сула носят лишь сугубо качественный характер > и не объясняют многих сторон явления дополнительного поглощения, в частности ширины области поглощения, ее структуры и рядадругих. Тем не менее работы Сула стимулировали быстрое развитие нового направления в исследовании магнитных кристаллов — нелинейного ферромагнитного резонанса. Широко поставленный эксперимент блестяще подтвердил теорию параметрического возбуждения ферромагнитного кристалла. Были созданы малошумящие параметрические усилители и пр. [19]. [c.384] Сахаро-фосфатная цепь нуклеиновой кислоты также не является сопряженной, и нуклеиновые кислоты — диэлектрики, ферромагнитные свойства, наблюдавшиеся методом электронного парамагнитного резонанса, оказались связанными с примесями железосодержащих соединений, от которых очень трудно избавиться. [c.110] Магнитная сепарация проводилась на приборе УЭМ-1Т при напряженности магнитного поля между клиновидными полюсами магнита 3,2-10 А/м. Кристаллы разделялись на две группы — магнитные (удаляемые полем с предметного столика) и немагнитные (остающиеся на предметном столике). Применение метода магнитного резонанса к немагнитной группе кристаллов не обнаружило в них ферромагнитных включений. Измерялись массы и разрушающие нагрузки кристаллов до сепарации Ро, магнитных Рм и немагнитных Рн групп. Результаты приведены в табл. 33. Из нее видно, что для первых трех партий кристаллов фракции 630/500 разрушающая нагрузка для немагнитной группы практически не отличается от исходной Ро- Более того, для партии с Яо = = 130 Н, разрушающая нагрузка для кристаллов магнитной группы несколько выше, чем для немагнитных. Следовательно, использо- [c.443] Ферромагнитный резонанс на кристаллах алмаза при использования ЭПР-спектрометра дает широкие полосы, причем форма спектров сложна, что не позволяет проводить количественные оценки. При ЭПР-измерениях было замечено, что с увеличением дефектности кристаллов (в частности, с увеличением содержания включений) наблюдаются уширение линий парамагнитного азота. Так, для немагнитных кристаллов, отсепарированных на сепараторе УЭМ-1Т, полуширина линий ЭПР дисперсного азота состав- [c.447] В заключение было проверено влияние температур прокалки порошков (800—1000° в течение 4 часов) на электромагнитные свойства ферритов. Образцы спекались пои температуре 1350° в течение 12 часов. Оказалось, что для рассмотренного интервала температур прокалки порошков удельный магнитный момент спеченных ферритов был равен магнитному моменту насыщения порошков. Остальные свойства ферритов (ширина полосы ферромагнитного резонанса, температура Кюри, удельное электросопротивление, плотность) также остались без изменений, несмотря на различный режим прокалки порошков. [c.229] Ширина линии ферромагнитного резонанса АЯ, э [c.564] Ферромагнитный резонанс и анизотропия. Ферриты-гранаты имеют меньшуюудельную намагниченность, чем ферриты-шпинели и большой интерес к ним был вызван в основном их уникальными свойствами в СВЧ-диапазоне. Минимальныезначения ширины линий ферромагнитного резонанса А Я =1 0,2 э были получены в иттриевом феррите-гранате, свободном от примесей редкоземельных ионов. [c.570] Ширина линии ферромагнитного резонанса АЯ. э, в некоторых редкоземельных ферритах со структурой граната [123] [c.578] Состав X из измерений намагниченности из ферромагнитного резонанса АН, а (Г = 3(10 К) Гс. "К гс-см Г—зоо к) [c.588] 46. Как экспериментально определить точку резонанса токов в цепи с ферромагнитными элементами? 47. Объясните работу ферромагнитного стабилизатора напряжений. Стабилизатор, у которого на зажимах нелинейного дросселя получают стабилизированное напряжение, является простейшим ферромагнитным стабилизатором. Его основной недостаток — низкий коэффициент мощности. Кроме того, при больших токах в цепи габариты линейного дросселя очень большие. Для уменьшения веса и габаритов ферромагнитные стабилизаторы напряжения изготовляют с объединенной магнитной системой, а для повышения коэффициента мощности включают конденсатор по схеме резонанса токов. Такой стабилизатор называется феррорезонансным. |

![рис. 29.8. кривые ферромагнитного резонанса для монокристалла мпд 89ре[ зд04 [24]. образец имел форму сферы диаметром 0,25 мм. Кривые сняты при комнатной температуре на частоте 9300 Мгц и соответствуют трем главным кристаллографическим направлениям, по которым направлено постоянное магнитное поле](12866_html_713a3028.png) <="" img="" >
<="" img="" >