Ответы на вопросы к экзамену. Вопросы к экзамену Как определить взаимные проводимости (расчетным и экспериментальным путем)

Название	Вопросы к экзамену Как определить взаимные проводимости (расчетным и экспериментальным путем)
Анкор	Ответы на вопросы к экзамену.docx
Дата	25.12.2017
Размер	0.74 Mb.
Формат файла
Имя файла	Ответы на вопросы к экзамену.docx
Тип	Вопросы к экзамену #12866
страница	4 из 5

1 2 3 4 5

Феррорезонансные стабилизаторы напряжения конструктивно похожи на обычные трансформаторы (рис. 1, а). Первичная обмотка w1 на которую подается входное напряжение Uвх, располагается на участке 2 магнитопровода, имеющем большое поперечное сечение для того, чтобы эта часть магнитопровода находилась в ненасыщенном состоянии. Напряжение Uвх создает магнитный поток Ф2.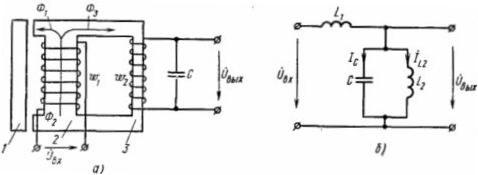

Рис. 1. Схемы феррорезонансного стабилизатора напряжения: а — принципиальная; б — замещения

Вторичная обмотка w2, на зажимах которой индуцируется выходное напряжение Uвых и к которой присоединяется нагрузка, расположена на участке 3 магнитопровода, имеющем меньшее сечение и находящемся в насыщенном состоянии. Поэтому при отклонениях напряжения Uвх и магнитного потока Ф2 значение магнитного потока Ф3 на участке 3 почти не изменяется, не изменяется э. д. с. вторичной обмотки и Uвых. При увеличении потока Ф2 та его часть, которая не может проходить по участку 3, замыкается через магнитный шунт 1 (Ф1).

Магнитный поток Ф2 при синусоидальном напряжении Uвх синусоидален. Когда мгновенное значение потока Ф2 приближается к амплитудному, участок 3 переходит в режим насыщения, поток Ф3 перестает увеличиваться и появляется поток Ф1. Таким образом, поток через магнитный шунт 1 замыкается только в те моменты времени, когда поток Ф2 по значению близок к амплитудному. Это делает поток Ф3 несинусоидальным, напряжение Uвых становится также несинусоидальным, в нем ярко выражена третья гармоническая составляющая.

В схеме замещения (рис. 1, б) параллельно включенные индуктивность L2 нелинейного элемента (вторичной обмотки) и емкость С образуют феррорезонансный контур, имеющий характеристики, представленные на рис 2. Как видно из схемы замещения, токи в ветвях пропорциональны напряжению Uвх. Кривые 3 (ветвь L2) и 1 (ветвь С) расположены в разных квадрантах, так как токи в индуктивности и емкости противоположны по фазе. Характеристику 2 резонансного контура строят, алгебраически суммируя токи в L2 и С при одних и тех же значениях напряжения Uвых.

Как видно из характеристики резонансного контура, применение конденсатора дает возможность получать стабильное напряжение при малых токах намагничивания, т. е. при меньших напряжениях Uвх.

Кроме того, при наличии конденсатора стабилизатор работает с высоким коэффициентом мощности. Что касается коэффициента стабилизации, то он зависит от угла наклона горизонтальной части кривой 2 к оси абсцисс. Так как этот участок имеет значительный угол наклона, то получить большой коэффициент стабилизации без дополнительных устройств невозможно.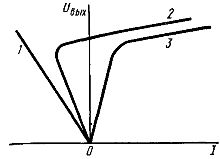

Рис. 2. Характеристики нелинейного элемента феррорезонансного стабилизатора напряжения

Таким дополнительным устройством является компенсирующая обмотка wк (рис. 3), располагаемая вместе с первичной обмоткой на ненасыщенном участке 1 магнитопровода. С увеличением Uвх и Ф увеличивается э. д. с. компенсирующей обмотки. Ее включают последовательно с вторичной обмоткой, но так, чтобы э. д. с. компенсирующей обмотки была противоположна по фазе э. д. с. вторичной обмотки. Если Uвх увеличивается, то незначительно увеличивается э. д. с. вторичной обмотки. Напряжение Uвых, которое определяется разностью э. д. с. вторичной и компенсирующей обмоток, поддерживается постоянным за счет возрастания э. д. с. компенсирующей обмотки.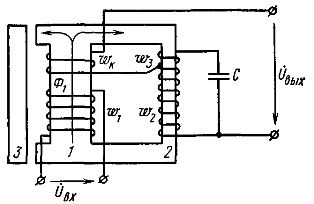

Рис. 3. Схема феррорезонансного стабилизатора напряжения с компенсационной обмоткой

Обмотка w3 предназначена для повышения напряжения на конденсаторе, что увеличивает емкостную составляющую тока, коэффициент стабилизации и коэффициент мощности.

Недостатками феррорезонансных стабилизаторов напряжения являются несинусоидальность выходного напряжения и зависимость его от частоты.

Промышленность выпускает феррорезонансные стабилизаторы напряжения мощностью от 100 Вт до 8 кВт, с коэффициентом стабилизации 20—30. Кроме того, выпускают феррорезонансные стабилизаторы без магнитного шунта. Магнитный поток Ф3 в них замыкается по воздуху, т. е. является потоком рассеяния. Это позволяет уменьшить вес стабилизатора, однако сужает рабочую область до 10% от номинального значения Uвх при коэффициенте стабилизации kc, равном пяти.

48. Покажите аналитическим путем зависимость индуктивности катушки с замкнутым сердечником от величины относительной магнитной проницаемости.
49. Изменится ли ток в катушке с ферромагнитным сердечником, подключенной к сети 220 В, если вынуть этот сердечник?

Возможно

50. Изменится ли магнитный поток в катушке с ферромагнитным сердечником, подключенной к сети 220 В, если вынуть этот сердечник?

Скорее всего

51. Изменится ли соотношение между падениями магнитного потенциала в стали и в зазоре катушки с ферромагнитным сердечником при изменении тока в катушке?

-
52. Нарисовать схему замещения катушки с ферромагнитным сердечником и объяснить, что учитывает каждый элемент в схеме
53. В чем заключается аналогия между электростатическим полем и полем постоянных токов? Продемонстрировать эту аналогию с помощью уравнений Максвелла. Какие величины, характеризующие поля являются подобными?

По своей природе электростатическое поле и электрическое поле постоянных токов в проводящей среде различны. Однако, между соотношениями, характеризующими эти поля, можно провести формальную аналогию.

Для удобства сопоставления выражений, относящихся к стационарному полю в проводящей среде и электростатическому полю в диэлектрике, представим их в виде табл. 2.1.

Таблица 2.1

Стационарное поле	Электростатическое поле
2	3

В пятой строке таблицы величина Di есть ток сквозь сечение s трубки тока, а величина Dq есть заряд на поверхности заряженного тела в начале трубки электрического смещения сечением также s.

Сравнивая соотношения, относящиеся к стационарному полю и электростатическому полю, можно отметить, что они формально совпадут, если в последних заменить вектор электрического смещения вектором плотности тока , электрический заряд Dq – током Di и абсолютную диэлектрическую проницаемость e – удельной проводимостью g.

Оба поля также удовлетворяют уравнению Лапласа. Но если два поля удовлетворяют одному и тому же уравнению и в них выполняются граничные условия для сходных величин, то при одинаковой форме граничных поверхностей совокупность эквипотенциальных и силовых линий в этих двух полях будет одинаковой (то есть, картины поля будут совпадать).

На этом и основан так называемый метод электростатической аналогии, позволяющий в ряде случаев при расчете поля в проводящей среде воспользоваться готовыми решениями соответствующих задач электростатики (и наоборот).

В частности, формулы для электрической проводимости сред, в которых протекает ток, могут быть получены из соответствующих формул для емкости тел, так как в аналогичных задачах ток заменяется зарядом. Электрическая емкость тела или емкость между телами определяется геометрическими параметрами тел и абсолютными диэлектрическими проницаемостями сред, окружающих тела. Поэтому, чтобы получить формулу для проводимости G, достаточно заменить в соответствующей формуле для С абсолютные диэлектрические проницаемости e диэлектриков – удельными проводимостями g проводящих сред. Например, в однородных средах для аналогичных задач будет соблюдаться соотношение

54. Обосновать возможность моделирования электростатического поля полем постоянных токов на проводящей бумаге?

Электрическое моделирование физических полей

Методы моделирования физических полей, основанные на аналогии уравнений, описывающих процессы в оригинале и модели, называются аналоговыми методами моделирования. Аналоговое моделирование связано с применением различных моделирующих устройств. Наибольшее распространение получили модели, основанные на аналогии исследуемых физических полей и электрического поля в проводящей среде. Методы, основанные на такой аналогии, называются электрическим моделированием. Эти методы можно разделить на две большие группы:

1) методы сплошных сред;

2) методы электрических сеток.

К методам сплошных сред можно отнести следующие: использование проводящей бумаги - для моделирования плоскопараллельных и осесимметричных полей в кусочно-однородных средах, описываемых уравнениями Лапласа, диффузии или волновым; использование металлических, графитовых, проводящих керамических и пластмассовых пластин, а также проводящей резины и ткани - для тех же задач; использование жидких электролитов, а также влажных дисперсных масс и желеобразных коллоидных материалов - для моделирования трехмерных полей в неоднородных случаях. Для моделирования физических полей, описываемых уравнениями с ненулевой правой частью, могут быть применены токовводы.

В качестве моделирующих электрических сеток используют LC, LR, RC и резистивные сетки. Правая часть в уравнениях математической физики моделируется включением источников тока в узлы сетки.

55. Как определяется емкость заряженных тел по результатам измерений на модели?

56. Как можно построить силовые линии поля по картине поля, содержащей только эквипотенциали?

Если φ₁= +60 В, а φ₂= – 60 В, то на линии, проходящей посередине между электродами φ = 0, а эквипотенциали справа от нее имеют значение –20В и–40 В, соответственно. Аналогично эквипотенциали слева от нее имеют значение +20 В и +40 В.

По картине поля можно в любой точке определить потенциал и напряженность электрического поля. Например, если исследуемая точка х находится посередине между эквипотенциалями φ₁= +20 В и φ₂= +40 В, то ее потенциал равен φ_х= +30 В. Для определения напряженности используем уравнение (23.3)

= –φ/l,

где l – расстояние между эквипотенциалями вблизи точки х. При этом направление вектора Е задаем примерно посередине между силовыми линиями (рис. 23.6).

По картине поля можно также определять емкость между заряженными телами. Обозначим число криволинейных квадратов в силовой трубке n, а число трубок m ( на рис.2.6 n=18, m=6). Разность потенциалов равна

φ₁ – φ₂=U=∫Edl=E₁ a₁ +E₂ a₂ +…=∑E_k a_k

Поток вектора Е в одной трубке равен V=E₁ b₁ l= E₂ b₂ l=…, где l– размер тел в направлении перпендикулярном чертежу.

По теореме Гаусса заряд определяется по формуле

q = ε∫Eds=εmV, где ε – диэлектрическая проницаемость среды между телами. Тогда емкость определяют по формуле

C=q/U=εml/(a₁/ b₁+ a₂ /b₂+…)=εmlb/na.

При равенстве a=bформула упрощается C=εml/n

58. Дайте определение потенциала электрического поля.

Потенциал электрического поля представляет собой отношение потенциальной энергии к заряду. Как известно электрическое поле является потенциальным. Следовательно, любое тело находящиеся в этом поле обладает потенциальной энергией. Любая работа, которая будет совершаться полем, будет происходить за счет уменьшения потенциальной энергии.

Формула 1 — Потенциал

Потенциал электрического поля это энергетическая характеристика поля. Он представляет собой работу которую нужно совершить против сил электрического поля для того чтобы переместить единичный положительный точечный заряд находящийся на бесконечности в данную точку поля.

Измеряется потенциал электрического поля в вольтах.

В случае если поле создается несколькими зарядами, которые расположены в произвольном порядке. Потенциал в данной точке такого поля будет представлять собой алгебраическую сумму всех потенциалов, которые создают заряды каждый в отдельности. Это так называемый принцип суперпозиции.

59. Дайте определение напряженности электрического поля.

Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы  действующей на неподвижный точечный заряд, помещенный в данную точку поля, к величине этого заряда :

.

Из этого определения видно, почему напряженность электрического поля иногда называется силовой характеристикой электрического поля (действительно, всё отличие от вектора силы, действующей на заряженную частицу, только в постоянном^[1] множителе).

В каждой точке пространства в данный момент времени существует свое значение вектора  (вообще говоря - разное^[2] в разных точках пространства), таким образом,  - это векторное поле. Формально это выражается в записи

$\vec e = \vec e(x,y,z,t),$

представляющей напряженность электрического поля как функцию пространственных координат (и времени, т.к.  может меняться со временем). Это поле вместе с полем вектора магнитной индукции представляет собой электромагнитное поле^[3], и законы, которым оно подчиняется, есть предмет электродинамики.

Напряжённость электрического поля в Международной системе единиц (СИ) измеряется в вольтах на метр [В/м] или в ньютонах на кулон [Н/Кл].

60. Дайте определение градиента.

Под градиентом скалярной функции понимают скорость изменения скалярной функции, взятой в направлении ее наибольшего возрастания. При этом в декартовой системе координат

(23.2)

Для сокращения записей различных операций над скалярными и векторными величинами употребляется дифференциальный оператор Гамильтона (оператор набла)

Другими словами, запись  эквивалентна записи grad, а “приписывание” слева к какой-либо скалярной функции (в нашем случае к ) оператора  означает взятие градиента от этой скалярной функции.

Подставим в уравнение Гаусса

уравнение (23.1). Получим

или

(23.3)

Уравнение (23.3) называется уравнением Пуассона. Частный вид уравнения Пуассона, когда _свб= 0, называется уравнением Лапласа. Уравнение Лапласа запишется так ² = 0, (23.4)

Оператор ² = div grad называют оператором Лапласа или лапласианом. В декартовой системе координат он равен

Тогда уравнение Пуассона в декартовой системе координат запишется следующим образом: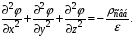

(23.5)

61. Что называется характеристическим сопротивлением фильтра?

Характеристическое сопротивление фильтра и его частотная зависимость определяют возможность наилучшего согласования с генератором и нагрузкой. Известная частотная зависимость характеристического сопротивления в полосе пропускания определяет возможность параллельной работы фильтров. [1]

Задано номинальное характеристическое сопротивление фильтра Ru и частота среза / с. Требуется определить параметры L и С Т - или П - образного фильтра нижних частот. [2]

62. Что такое коэффициент затухания, в каких единицах он измеряется?

Это дифференциальное уравнение, описывающее колебания заряда конденсатора. Введем обозначения:

                       ,                     (3.46)

Величину β также как и в случае механических колебаний называют коэффициентом затухания, а ω₀ – собственной циклической частотой колебаний.

С введенными обозначениями уравнение (3.45) примет вид

                                            (3.47)

Уравнение (3.47) полностью совпадает с дифференциальным уравнением гармонического осциллятора с вязким трением (формула (4.19) из раздела "Физические основы механики"). Решение этого уравнения описывает затухающие колебания вида

                         q(t) = q₀e^-btcos(wt + j)                (3.48)

где q₀ – начальный заряд конденсатора, ω = – циклическая частота колебаний, φ – начальная фаза колебаний. На рис. 3.17 показан вид функции q(t). Такой же вид имеет и зависимость напряжения на конденсаторе от времени, так как U_C = q/C.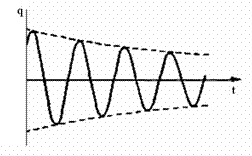

Рис. 3.17

Из рисунка видно, что амплитуда затухающих колебаний убывает со временем. Характеристикой затухания являетсявремя релаксации τ. Промежуток времени t = 1/b - это время, в течение которого амплитуда колебаний уменьшается в е раз. Затухание колебаний характеризуют также логарифмическим декрементом затухания λ

                         l = ln[A(t)/A(t+T)] = bT= T/t                (3.49)

где А(t) – текущая амплитуда колебаний (А(t) = q₀e^-bt), Т – период колебаний. По своему смыслу величина, обратная T/t определяет число колебаний N_e, совершаемых за время релаксации. Следовательно, логарифмический декремент затухания - величина, обратная числу N_e.

Для характеристики качества колебательного контура вводят величину Q, называемую добротностью

                         Q = π/λ = πN_e                           (3.50)

Таким образом, добротность показывает, насколько медленно затухают колебания в контуре.

Из (3.50), (3.49) и (3.46) можно получить выражение для добротности контура через его электрические характеристики

                         Q =                               (3.51)

Описанный колебательный процесс в контуре совершается без каких-либо внешних воздействий за счет начального запаса энергии, сообщенного контуру. Такие колебания называют свободными. Электрическое сопротивление проводников приводит к затуханию свободных колебаний. Для получения незатухающих колебаний необходимо пополнять убыль энергии в контуре за счет внешних источников. Это можно осуществить, например, включив в состав контура источник переменной э.д.с. Е (рис. 3.18).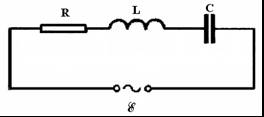

63. Что такое коэффициент фазы? Как он зависит от частоты?

Коэффициент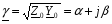

(20.11)

называют постоянной распространения; в нем α – коэффициент затухания, β – коэффициент фазы.

Коэффициент затуханияα характеризует затухание падающей волны на единицу длины линии (на 1 км), а коэффициент фазы β– изменение фазы падающей волны на единицу длины линии. Ток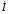

определим из уравнения (7.15):

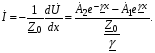64. Почему коэффициент затухания, определяемый экспериментально, не равен нулю во всей полосе пропускания?

65. Что понимают под согласованной нагрузкой фильтра?

Что такое согласованная нагрузка

1 2 3 4 5