Ответы на вопросы к экзамену. Вопросы к экзамену Как определить взаимные проводимости (расчетным и экспериментальным путем)
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
Ответы на вопросы к экзамену 1. Как определить взаимные проводимости (расчетным и экспериментальным путем)? Коэффициенты с разными индексами gmn называют взаимными проводимостями (или передаточными). Взаимная проводимость gmn равна току в ветви m при действии единственной ЭДС, равной 1 В и включенной в ветви n, когда в остальных ветвях отсутствуют ЭДС и источники токов. Взаимные проводимости можно определять опытным путем. Для этого из исследуемой цепи удаляют все источники ЭДС и источники токов, кроме одной ЭДС в нужной ветви Ek. Измерив, токи Ik и Im, рассчитывают взаимную проводимость gmk=Im/Ek и входную проводимость gkk=Ik/Ek. 2. В чем заключается принцип линейности? Как определить соответствующие коэффициенты. Принцип линейности. Если в линейной электрической цепи изменяется ЭДС или сопротивление в какой-либо одной цепи, то две любые величины (U или I) двух любых ветвей связаны друг с другом линейными зависимостями вида y=a+bx (3.1) т.е. U=a+bI или U1=c+dU2 или I1=k+mI2. Аналогичная зависимость получается при изменениях этих величин в двух ветвях, тогда y=a+bx+cz. (3.2) Коэффициенты а, b в уравнении (3.1) определяются расчетным путем или экспериментально. Для этого нужно знать напряжения (или токи) для двух различных режимов. Подставляя эти значения в уравнение 3.1, получим систему двух уравнений с двумя неизвестными. Решая систему уравнений, определим коэффициенты а, b. Аналогично, для определения коэффициентов а, b, c в уравнении 3.2 необходимо иметь данные для трех режимов и решить систему из трех уравнений. Следует иметь в виду, что в качестве у, x, z могут фигурировать только U и I, но ни в коем случае R. 3. Как определить для разветвленной цепи опытным путём параметры эквивалентного генератора? Рис.3.1 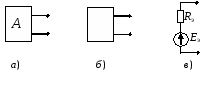 Электрическую схему, содержащую два выходных конца (зажима), называют двухполюсником. Если внутри этой схемы имеются источники, то такой двухполюсник называют активным (рис. 3.1, а), если источников нет, то – пассивным (рис. 3.1, б). Электрическую схему, содержащую два выходных конца (зажима), называют двухполюсником. Если внутри этой схемы имеются источники, то такой двухполюсник называют активным (рис. 3.1, а), если источников нет, то – пассивным (рис. 3.1, б). Покажем, что активный двухполюсник можно заменить эквивалентным генератором (рис. 3.1, в), у которого Eэ равно напряжению холостого хода на разомкнутых зажимах двухполюсника, а сопротивление Rэ – входному сопротивлению двухполюсника. Для этого некоторую схему представим в виде активного двухполюсника (рис. 3.2, а) и присоединенной к нему ветви с током I (рис. 3.2, б). Включим в эту ветвь две ЭДС, равные по величине, но Рис.3.2. Двухполюсники: а–активный; б–с нагрузкой; в– преобразование к эквивалентному генератору а) б) в) 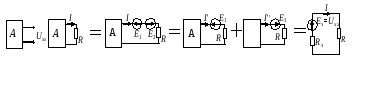 встречно направленные (ток I при этом не изменится). встречно направленные (ток I при этом не изменится). Представим ток I как сумму токов I΄, учитывающую все ЭДС схемы и E1, а также тока I΄΄, учитывающего только E2 (это следует из уравнений 2.2, 2.3). Выберем величину включенных ЭДС равной величине напряжения холостого хода Uхх, когда двухполюсник отключен от R (рис. 3.2, а). Тогда ток  , а ток , а ток 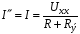 , где RЭ – сопротивление двухполюсника (его определяют, исключив из схемы, представленной двухполюсником, все источники тока и ЭДС). , где RЭ – сопротивление двухполюсника (его определяют, исключив из схемы, представленной двухполюсником, все источники тока и ЭДС). Совокупность эквивалентного сопротивления и источника ЭДС величиной EЭ (равной напряжению холостого хода двухполюсника) можно рассматривать, как некоторый эквивалентный генератор с внутренним сопротивлением RЭ и ЭДС, равной EЭ=Uхх. Расчет тока в некоторой ветви разветвленной электрической схемы сводится к замене части схемы, не содержащей требуемую ветвь, эквивалентным генератором и последующему определению тока  . .Найти параметры эквивалентного генератора можно экспериментально и расчетным путем (если известны сопротивления и ЭДС двухполюсника). Для экспериментального определения нужно измерить напряжение на разомкнутых зажимах двухполюсника (тем самым определим Uхх и EЭ), а затем замкнуть зажимы двухполюсника накоротко и измерить ток короткого замыкания. Тогда сопротивление эквивалентного генератора  . .Если можно ожидать недопустимо большого тока короткого замыкания, то замыкают двухполюсник на известное сопротивление R, и тогда, измерив 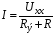 , находят , находят 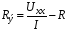 . .Расчетным путем параметры эквивалентного генератора находят следующим образом:
4. Условие получения максимума мощности в сопротивлении. В автоматике при наличии маломощных датчиков возникает проблема передачи максимума мощности нагрузке. Заменим датчик эквивалентным генератором, имеющим ZЭ= RЭ +jXЭ. Тогда ток в нагрузке 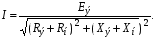 Если выбрать реактивные сопротивления противоположных характеров, т.е. одно емкостное, а другое индуктивное, то jXэ–jXн=0. При этом в цепи будет резонанс напряжений и ток достигнет максимального значения 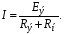 Для получения максимума активной мощности в нагрузке 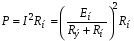 необходимо производную 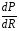 приравнять нулю и определить RН=RЭ (аналогично тому, как это было в цепях постоянного тока). приравнять нулю и определить RН=RЭ (аналогично тому, как это было в цепях постоянного тока).Таким образом, максимум мощности в нагрузке получается при jXН=–jXЭ, RН=RЭ или ZН=ZЭ*, т.е. когда комплексное сопротивление нагрузки равно сопряженному значению комплексного сопротивления эквивалентного генератора. Если активное сопротивление нагрузки не равно активному сопротивлению генератора, то используют согласующий трансформатор. При этом, как отмечалось выше, входное сопротивление трансформатора  . .В этом случае условие получения максимума в нагрузке достигается при 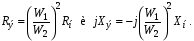 Для достижения последнего условия используется включение в цепь нагрузки конденсатора. Следует отметить, что коэффициент полезного действия при этом будет равен 0,5. В электроснабжении при передаче больших мощностей задачи ставятся иначе – необходимо иметь минимальные потери в линии и высокий коэффициент полезного действия. Достигается это повышением напряжения в линии электропередачи. Обозначив сопротивлении линии ZЛ= RЛ + jXЛ, определим падение напряжения в линии: 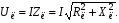 Потребителей обычно интересует другая величина – потеря напряжения 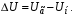 Обычно потеря напряжения меньше падения напряжения в линии. 5. В электротехнике принято фазовое определение резонанса. Как это понимать? В электрической цепи, содержащей разнородные реактивные элементы (L и C), возможны резонансные режимы, когда напряжение и ток совпадают по фазе. При этом входное сопротивление такой цепи будет чисто активным, а реактивная мощность равна нулю. Рассмотрим два различных режима: А. Резонанс токов В электрической цепи, образованной двумя параллельными ветвями с разнородными реактивными сопротивлениями, возникает резонанс токов при равенстве реактивных проводимостей этих ветвей bL=bC. Тогда суммарный ток (рис. 6.2) равен 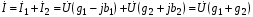 . .Итак, при резонансе токов должно быть: а) совпадение по фазе напряжения с полным током, б) равенство реактивных проводимостей в параллельных ветвях; при этом суммарный ток может оказаться меньше токов в ветвях. 6. Как определяется добротность контура? – характеризует качество колебательного контура, обозначается Q. Численно равна отношению напряжения на любом из реактивных участков на резонансе к напряжению, подводимому к контуру, или отношению реактивного сопротивления к активному. При большой добротности контура напряжение на нем значительно превышает напряжение на входе контура. 7. Какие величины равны друг другу при резонансе? В электрической цепи, содержащей разнородные реактивные элементы (L и C), возможны резонансные режимы, когда напряжение и ток совпадают по фазе. При этом входное сопротивление такой цепи будет чисто активным, а реактивная мощность равна нулю. Рассмотрим два различных режима: А. Резонанс токов В электрической цепи, образованной двумя параллельными ветвями с разнородными реактивными сопротивлениями, возникает резонанс токов при равенстве реактивных проводимостей этих ветвей bL=bC. Тогда суммарный ток (рис. 6.2) равен 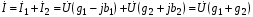 . .8. Нарисуйте векторную диаграмму при резонансе токов. 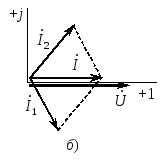 9. Дать определение резонанса токов. Какие величины равны друг другу при резонансе? резонанс, происходящий в параллельном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает ссобственной частотой контура. 10. Может ли ток в одной из ветвей цепи переменного тока быть больше чем суммарный ток? Пояснить с помощью 1 закона Кирхгофа. что при относительно малых активных проводимостях ветвей суммарный ток может оказаться меньше любого тока в ветвях, т.е. I<I1 и I<I2. При отсутствии активных сопротивлений в ветвях суммарный ток стремится к нулю, в то время как токи ветвей могут быть значительными. Итак, при резонансе токов должно быть: а) совпадение по фазе напряжения с полным током, б) равенство реактивных проводимостей в параллельных ветвях; при этом суммарный ток может оказаться меньше токов в ветвях. Возможность уменьшить суммарный ток используется в промышленности, где преобладают потребители с активно-индуктивными сопротивлениями. Подключая батарею конденсаторов параллельно приемникам в цеху или на предприятии, удается снизить суммарный ток и, тем самым, уменьшить потери энергии в генераторах и линии электропередачи. При этом угол сдвига фаз между током и напряжением уменьшается. На рис. 6.2, в представлена векторная диаграмма для иллюстрации подобной ситуации. В исходном состоянии цех потреблял ток I1, и угол сдвига фаз между напряжением U и током I1 был равен φ. После подключения батареи конденсаторов цех стал потреблять суммарный ток I (меньше чем I1) и угол сдвига фаз уменьшился до φзад (обычно стремятся получить cosφзад = 0,9…0,95). Следует отметить, что ток потребителей цеха I1 при этом не изменился. 11. Как экспериментально определяется коэффициент взаимной индукции? 7.1. Определение взаимной индуктивности В том случае, когда изменение тока в одном из элементов цепи приводит к появлению ЭДС в другом элементе цепи, говорят, что эти два элемента индуктивно связаны, а возникающую ЭДС называют ЭДС взаимной индукции. На рис. 7.1, а схематично представлено распределение магнитных потоков у двух близко расположенных индуктивных катушек. У магнитного потока первой катушки Ф1 часть потока Ф11 связана (сцеплена) с витками этой катушки, а часть потока Ф12 пронизывает вторую катушку, т.е. Ф1= Ф11 + Ф12. 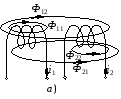 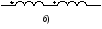  Рис. 7.1 У второй катушки Ф2 = Ф22 + Ф21. В итоге потокосцепление первой катушки w1 (Ф11 + Ф12+ Ф21) = 11 + 12+21= 1 +21. Аналогично потокосцепление у второй катушки w2 ( Ф2+ Ф12 ) = 2+ 12. Часть потока от соседней катушки может оказаться со знаком плюс, когда потоки направлены согласно, или со знаком минус, когда потоки направлены встречно. Потокосцепление 21 пропорционально току i2, а 12– току i1, т.е. 21 = w1Ф21 = M21i2 = Mi2, 12 = w12Ф12 = M12i1 = Mi1. Коэффициент пропорциональности М (Гн) называют взаимной индуктивностью. Доказывается, что М = М21= М12. При изменении токов в катушках наводятся ЭДС 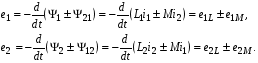 Их называют соответственно eL – ЭДС самоиндукции, eM– ЭДС взаимоиндукции. Для оценки степени индуктивной связи вводят коэффициент связи 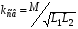 . Коэффициент связи всегда меньше единицы. . Коэффициент связи всегда меньше единицы.Магнитная энергия двух индуктивно связанных катушек 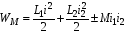 . .Чтобы знать, согласно или встречно включены катушки, делают разметку их концов. На схемах начала обмоток обозначают точкой или звездочкой (рис. 7.1, б). Выполнить разметку концов и определить взаимную индуктивность можно экспериментально. Для этого включают обе катушки последовательно под напряжение U. Если катушки включены согласно, то уравнение напряжений будет иметь вид:  , ,или в комплексном виде  Если катушки включены встречно, то Если катушки включены встречно, то Легко видеть, что при встречном включении полное сопротивление цепи меньше и при неизменном напряжении ток будет больше, чем при согласном включении. Это служит критерием для разметки концов катушек. Для определения величины взаимной индуктивности найдем  . .Можно определить взаимную индуктивность и другим способом (рис. 7.1, в). На разомкнутых концах второй катушки измеряется напряжение, равное ЭДС взаимоиндукции и пропорциональное току в первой катушке  тогда тогда  . .12.Как экспериментально определяются одноимённые концы индуктивно-связанных катушек? Магнитная энергия двух индуктивно связанных катушек 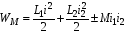 . .Чтобы знать, согласно или встречно включены катушки, делают разметку их концов. На схемах начала обмоток обозначают точкой или звездочкой (рис. 7.1, б). Выполнить разметку концов и определить взаимную индуктивность можно экспериментально. Для этого включают обе катушки последовательно под напряжение U. Если катушки включены согласно, то уравнение напряжений будет иметь вид:  , ,или в комплексном виде 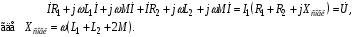 Если катушки включены встречно, то Если катушки включены встречно, то Легко видеть, что при встречном включении полное сопротивление цепи меньше и при неизменном напряжении ток будет больше, чем при согласном включении. Это служит критерием для разметки концов катушек. Для определения величины взаимной индуктивности найдем 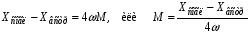 . .Можно определить взаимную индуктивность и другим способом (рис. 7.1, в). На разомкнутых концах второй катушки измеряется напряжение, равное ЭДС взаимоиндукции и пропорциональное току в первой катушке  тогда тогда 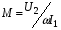 . .13. Как рассчитать коэффициент индуктивной связи? Для оценки степени индуктивной связи вводят коэффициент связи 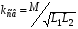 . Коэффициент связи всегда меньше единицы. . Коэффициент связи всегда меньше единицы.14. Как экспериментально определить индуктивность реле обмотки? В техническом устройстве, например в обмотке реле, при протекании электрического тока не только создается магнитное поле, но и происходит ее нагрев, т.е. преобразование энергии электрического поля в тепловую. Поэтому схема замещения реле будет представлена двумя идеализированными элементами R и L. Источники электрической энергии (аккумуляторы, генераторы и т.д.) характеризуются внешней характеристикой (рис. 1.3, а), представляющей зависимость напряжения на зажимах источника от тока, отдаваемого им в нагрузку. 15. Как проводится «развязка» индуктивно связанных обмоток? В том случае, когда изменение тока в одном из элементов цепи приводит к появлению ЭДС в другом элементе цепи, говорят, что эти два элемента индуктивно связаны, а возникающую ЭДС называют ЭДС взаимной индукции. 16. Нарисуйте схему замещения трансформатор без индуктивных связей. На рис. 7.5, в дана приведенная схема замещения трансформатора, в которой, кроме «развязывания», вторичная цепь приведена к первичной, исходя из следующих уравнений: 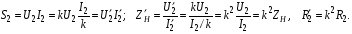 Выбирая 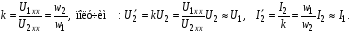 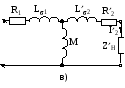 17. Что такое «вносимое сопротивление». Отчего оно зависит? Запишем уравнения трансформатора в комплексной форме  Решая эти уравнения, найдем: 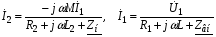 , ,где 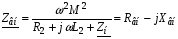 – вносимое сопротивление из вторичной цепи в первичную. – вносимое сопротивление из вторичной цепи в первичную.При изменении сопротивления нагрузки (ток I2 возрастает) возрастает вносимое сопротивление, поскольку его индуктивное сопротивление Xвн входит со знаком минус, оно уменьшает входное сопротивление трансформатора, что приводит к увеличению тока I1. Найдем комплексную мощность, обусловленную взаимной индукцией,  . .Аналогично  . .При этом  . .Если π >φ1 >0, то P1M >0, т.е. активная мощность передается из первичной обмотки во вторичную. 18. В схеме звезда с нейтральным проводом был симметричный режим и вдруг произошел обрыв фазного провода. Назовите, что изменилось и в какую сторону. Звезда-звезда с нейтральным проводом. Обрыв фазного провода (например, фазы А). В этом режиме напряжения на нагрузках, включенных в другие фазы, не изменятся, но появится ток в нейтральном проводе. Короткое замыкание нагрузки в одной из фаз (Zа=0). Это тяжелый аварийный режим, приводящий к резкому возрастанию тока в этой фазе  и в нейтральном проводе, что ведет к пожарам и перегоранию проводов на нагрузке, или нейтрального провода, который выполняют более тонким. После разрыва нейтрального провода возникает режим короткого замыкания нагрузки в одной из фаз, рассмотренный выше. и в нейтральном проводе, что ведет к пожарам и перегоранию проводов на нагрузке, или нейтрального провода, который выполняют более тонким. После разрыва нейтрального провода возникает режим короткого замыкания нагрузки в одной из фаз, рассмотренный выше.Нагрузка включена треугольником. В этой схеме возможны обрыв фазного, линейного проводов и короткое замыкание нагрузки. Обрыв фазного провода (Zab=). В этом режиме токи и напряжения в других фазах нагрузки не изменяются, а линейные токи Iaи Ib станут равны фазным токам, т.е. уменьшатся в  раза. Линейный ток Ic не изменится (рис. 10.5, а) раза. Линейный ток Ic не изменится (рис. 10.5, а)   Рис. 10.5 Обрыв линейного провода (например, А). В этом режиме ток и напряжение на нагрузке Zbc не изменится, а на нагрузках Zabи Zca уменьшатся в 2 раза, так как они оказываются включенными последовательно под то же напряжение UBC (рис. 10.5, в). Линейные токи IB и IC будут равны 1,5Iф и, следовательно, уменьшатся по сравнению с исходным симметричным режимом, когда они были равны  (рис. 10.5, в). (рис. 10.5, в).Короткое замыкание нагрузки в одной из фаз (Zab=0). Это тяжелый аварийный режим, при котором резко возрастает ток в фазе ab  и в линейных проводах А и В, что приводит к пожарам и перегоранию проводов (обычно в этой фазе). и в линейных проводах А и В, что приводит к пожарам и перегоранию проводов (обычно в этой фазе).19. В схеме звезда без нейтрального провода был симметричный режим и вдруг произошел обрыв фазного провода. Назовите, что изменилось и в какую сторону. Звезда-звезда без нейтрального провода.. Обрыв фазного провода (например, фазы А). В этом режиме нагрузки ZBи ZC в двух других фазах оказываются включенными последовательно под линейное напряжение. Напряжение на нагрузках (при их равенстве) станет  и, следовательно, уменьшится в и, следовательно, уменьшится в  раз. При этом появится смещение нейтрали (напряжение между раз. При этом появится смещение нейтрали (напряжение между  нулевыми точками генератора и нагрузки), равное нулевыми точками генератора и нагрузки), равное  (рис. 10.4, а). В месте разрыва напряжение UAO' возрастет в 1,5 раза и станет равным 1,5Uф (рис. 10.4, а). (рис. 10.4, а). В месте разрыва напряжение UAO' возрастет в 1,5 раза и станет равным 1,5Uф (рис. 10.4, а).Короткое замыкание нагрузки в одной из фаз (Za=0). В этом режиме сопротивления нагрузки других фаз оказываются включенными под линейное напряжение  , т.е. напряжения и токи в нагрузке возрастут в , т.е. напряжения и токи в нагрузке возрастут в  раз. При этом смещение нейтрали станет равным U0'0=Uф=UAO (рис. 10.4, б). раз. При этом смещение нейтрали станет равным U0'0=Uф=UAO (рис. 10.4, б).20. В схеме звезда с нейтральным проводом был симметричный режим и вдруг произошло короткое замыкание нагрузки в фазе А. Назовите, что изменилось и в какую сторону. Звезда-звезда с нейтральным проводом. Обрыв фазного провода (например, фазы А). В этом режиме напряжения на нагрузках, включенных в другие фазы, не изменятся, но появится ток в нейтральном проводе. Короткое замыкание нагрузки в одной из фаз (Zа=0). Это тяжелый аварийный режим, приводящий к резкому возрастанию тока в этой фазе  и в нейтральном проводе, что ведет к пожарам и перегоранию проводов на нагрузке, или нейтрального провода, который выполняют более тонким. После разрыва нейтрального провода возникает режим короткого замыкания нагрузки в одной из фаз, рассмотренный выше. и в нейтральном проводе, что ведет к пожарам и перегоранию проводов на нагрузке, или нейтрального провода, который выполняют более тонким. После разрыва нейтрального провода возникает режим короткого замыкания нагрузки в одной из фаз, рассмотренный выше.21. При каких условиях можно вести расчет трехфазной цепи «на одну фазу». Трехфазная цепь является частным случаем разветвленной цепи переменного тока, и для ее расчета могут быть применены рассмотренные выше методы расчета. Для симметричных трехфазных цепей расчеты упрощаются. Звезда-звезда. Простейшее соединение симметричной нагрузки получим, включив одинаковые приемники Z между каждой фазой и нейтралью. Такая цепь с выбранными положительными направлениями токов показана на рис. 9.3, а, гдеZф – сопротивления соединительных фазных проводов, 0и0– нейтральные (нулевые) точки генераторов и нагрузки, Z0 – сопротивление соединяющего их нейтрального провода. Естественно предположить из соображений симметрии, что токи в фазных проводах (  одинаковы по величине и последовательно смещены по фазе на 120, т.е. одинаковы по величине и последовательно смещены по фазе на 120, т.е.  , а ток в нейтральном проводе , а ток в нейтральном проводе  поскольку 1+а+а2=0. Но если это так (т.е. IN=0), то потенциалы точек 0и 0' совпадают. Следовательно, полное фазное напряжение генератора подается на последовательно включенные сопротивления Zф и Z и по закону Ома поскольку 1+а+а2=0. Но если это так (т.е. IN=0), то потенциалы точек 0и 0' совпадают. Следовательно, полное фазное напряжение генератора подается на последовательно включенные сопротивления Zф и Z и по закону Ома Это позволяет вести расчет для одной фазы. В других фазах токи и напряжения будут такие же, но сдвинуты на угол 120˚. При этом в схеме для расчета на одну фазу (рис.9.4,б) сопротивление в нейтральном проводе отсутствует, т.к. ток в нейтральном проводе симметричной трехфазной цепи равен нулю. Определив напряжения на сопротивлениях фазы  можно построить диаграмму напряжений для этой фазы (рис.9.4,в) или сразу диаграмму напряжений для трехфазной цепи (рис.9.4,г).   Z Zф А О а б) UА О' UаО’ I в) UАа UА Рис. 9.4 Отсутствие тока в нейтральном проводе при симметричной нагрузке позволяет применять схемы «звезда-звезда без нейтрального провода» для заведомо симметричной нагрузки (например, для трехфазных двигателей). Расчет такой цепи выполняется аналогично рассмотренному выше: составляется схема для одной фазы, определяются напряжения на сопротивлениях фазы и затем строится векторная диаграмма трехфазной цепи. Нагрузка включена треугольником. В этой схеме (рис.9.5,а) напряжения на фазах нагрузки равны линейным напряжениям генератора Uab =UAB= Uл. Если сопротивлением проводов можно пренебречь, то линейные токи в нагрузке равны (рис.9.5,б)   Обычно векторную диаграмму токов строят, переместив фазные токи в центр тяжести треугольника фазных напряжений (рис. 9.5,в). Тогда линейные токи образуют треугольник (рис. 9.5, в). b а с Iab Zac Zab Zbc Ibc Iac Ib Ia a)  Рис. 9.5  Для наглядности диаграмма (рис. 9.5,в) построена для случая, когда сопротивления нагрузки активные Z = R. Тогда фазные токи Iab, Ibc, Ica на диаграмме параллельны фазным напряжениям Uab, Ubc, Uca, а линейные токи Ia, Ib, Ic определяются как разность фазных токов и образуют треугольник, повернутый относительно треугольнику напряжения на угол 30о. Для наглядности диаграмма (рис. 9.5,в) построена для случая, когда сопротивления нагрузки активные Z = R. Тогда фазные токи Iab, Ibc, Ica на диаграмме параллельны фазным напряжениям Uab, Ubc, Uca, а линейные токи Ia, Ib, Ic определяются как разность фазных токов и образуют треугольник, повернутый относительно треугольнику напряжения на угол 30о.В тех случаях, когда сопротивление линейных проводов нельзя пренебречь (рис. 9.5, г), для расчета цепи заменяют схему треугольника на схему звезда. При этом сопротивление нагрузки в схеме звезда уменьшают в 3 раза. Получается схема аналогична схеме на рис. 9.4, в. Она также как и та рассчитывается на одну фазу. При этом сразу определяются линейные токи Ia, Ib, Ic. Фазные токи по модулю в √3раз меньше линейных и отстают от них на угол 30о. 22. Как рассчитать фазный ток, если известны линейное напряжение и сопротивление нагрузки в схеме треугольник. Схема треугольник В этой схеме (рис. 10.2,) токи в фазах при несимметричной нагрузке различны    но напряжения остаются неизменными (номинальные). Линейные токи определяют по закону Кирхгофа но напряжения остаются неизменными (номинальные). Линейные токи определяют по закону Кирхгофа Мощность трехфазной несимметричной цепи. Для измерения активной мощности трехфазной нагрузки в общем случае, когда нагрузка несимметрична, используют 3 ваттметра (рис. 10.3, а), и тогда полная мощность равна сумме показаний ваттметров. При симметричной нагрузке достаточно одного ваттметра, включенного в одну из фаз. Трехфазную цепь стремяпроводами, соединяющими генератор с потребителем, всегда можно рассматривать как две двухпроводные линии, имеющие один общий провод, например как линии АВ и СВ с общим проводом В (рис. 10.3, б), в котором ток  . При этом по первой линии при напряжении . При этом по первой линии при напряжении  идет ток идет ток  , а по второй линии при напряжении , а по второй линии при напряжении  идет ток идет ток  . .  Рис. 10.3 Мощность, передаваемая по первой линии  , , а мощность, передаваемая по второй линии,  Полная мощность, передаваемая по трехпроводной линии, S=S1+S2. Из сказанного вытекает возможность измерять мощность, передаваемую по трехпроводной линии трехфазной системы, двумя ваттметрами, каждый из которых определяет мощность, передаваемую по одной из двух двухпроводных линий. Такая схема включения ваттметров (схема Арона) изображена на рис. 10.3, б. При выводе не делалось никаких предположений о симметрии системы, следовательно, найденный метод измерения мощности двумя ваттметрами применим как в случае симметричной, так и в случае несимметричной трехфазной трехпроводной системы. При чисто активной нагрузке (=0) показания обоих ваттметров одинаковы. Полное значение передаваемой (активной) мощности равно алгебраическойсумме показаний обоих ваттметров. На практике часто два ваттметра ставятся на общую ось. Показания такого сдвоенного ваттметра непосредственно равны всей (активной) мощности, передаваемой по трехпроводной линии. Если определить разность показаний ваттметров W2–W1=UЛIЛsin, то по ней можно определить реактивную мощность  . На основании последних выражений легко вывести формулу, позволяющую определить угол по показаниям ваттметров: . На основании последних выражений легко вывести формулу, позволяющую определить угол по показаниям ваттметров:  23. Как определяется мощность в трёхфазных цепях?. |
