ВОПРОСЫ К ЭКЗАМЕНУ ПО ТЕОРИИ АВТОМАТОВ. Вопросы к экзамену Строки. Префиксы, суффиксы, подстроки. Формальные языки
 Скачать 3.16 Mb. Скачать 3.16 Mb.
|
6.
6.Вопросы к экзамену Строки. Префиксы, суффиксы, подстроки. Формальные языки. Строка – это конечная последовательность символов а1, а2,…,аn, каж-й из кот-х принадлежит некоторому конечному алф-ту сигма Σ, при этом символы в строке могут повторяться. Пустой строкой наз-т ε-строку ее длина-ноль, т.е. без единого символа. (не=пробелу). |x|=m-длина строки, т.е. строка содержит m символов. Пусть Σ-некот-й алф-т, обозначим Σ* мн-во опред-х над этим алф-м строк. Для Σ={0,1}; Σ*= {ε,0,1,01,11,10,101,…} видно, что н-во Σ* - предс-т собой бесконечное счетное мн-во элем-в, ε-строка всегда 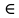 Σ*. Σ*.Пусть сущ-т строка х 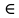 Σ* и |x|=m. Пусть сущ-т строка y Σ* и |x|=m. Пусть сущ-т строка y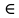 Σ* и |y|=n, тогда объединение строк ху им. длину |xy|=m+n – конкатенация. Σ* и |y|=n, тогда объединение строк ху им. длину |xy|=m+n – конкатенация.Если х= а1, а2,…,аm; у= b1, b2,…,bn то |xy|= а1а2…аmb1b2...bn Объединение – ассоциативная операция, но не коммуникативная. Если некоторая срока z м.б. представлена как объединение строк х и у: z=ху, то строку х наз-т префиксом строки z, а строку у-суффиксом. Если строка z т.ч. ее м/о представить как объединение 3х строк z=xwy, то строка w н-ся подстрокой строки z. //z=аcab префиксы: ε,a,ac,aca,acab суффиксы: ε,b,ab,cab,acab подстроки: ε,a,b,c,ac,ca,ab,aca,cab,acab Разв-е теории и ср-в искус. интелекта позволяет надеяться на то, что взаимод-е чел-ка и ком-ра в недалеком будущем буд/т осуществляться на языке, близком к естественному. Но в наст. время, прог-ты в основном описывают задачи на формальных языках, на языках высокого уровня и иногда на ассемблере. Прог-мы, написанные на алгоритмических языках становятся доступными ком-ру, т/о после их трансляции, т.е. преобразования команд выс. ур/ня в машинные инструкции. Теория построения трансляторов базируется на теории формальных языков, особенно в части синтакс. и семантического разбора. (семантика – смысл, синтаксис – грамматика). Формальным языком L над алф-ом Σ н-ся произвольное подмн-во мн-ва Σ*. Если L1 и L2 это 2а формальных языка, то их объединение есть нов.форм.язык, т.ч.L= L1L2{xy| х 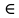 L1,у L1,у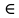 L2 } операция объединения формальных строк – ассоциативная операция, но не коммуникативная. L2 } операция объединения формальных строк – ассоциативная операция, но не коммуникативная.Для произвольного формального языка L справедливо // L1={0,01} и L2={ε,0,10}значит L= L1L2={0,01,00,010,010,0110} L0= ε, L1=L, L2=L*L -объединение форм. языка L с самим собой:  Дерево вывода. Синтаксическое и семантическое деревья. Примеры. Правила, определяющие мн-ва текстов образ-т синтаксис языка, а описание мн-ва смыслов и соответствий м/у текстами и смыслами – семантику языка. Если в ест.языке допуск-ся некорректности в синтаксисе и м.б.понятен смысл предложения, то в формальных языках предложение в первую очередь должно быть правильным синтаксически. Ф-ла Бэкуса-Наура(БНФ) исп-ся для описания синтаксиса языков прогр-ия, она использует след-щие 4 символа: ::= присвоить; 2) < - открыть; 3) > - закрыть; 4) | - или //пр-р: The man drives a car. <прост. предложение>::=<подфраза сущ.><глагол><подфр.сущ.>; <подфраза сущ-го>::=<артикль><имя сущ-ое>; <имя сущ-ое>::= man, <имя сущ-ое>::=car, <артикль>::=the, <артикль>::=a, <глагол>::=drives Связи, задаваемые ф-лой Б-Н м.б.представлены и графически в виде дерева-вывода: 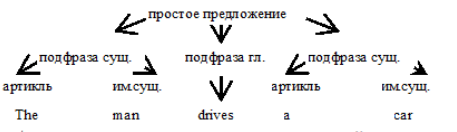 м/о построить мн-во простых предложений, удовлетворяющих дан.структуре и синтаксически правильных, но не все они буд.им.смысл.( The car drives a man).Таким образом, в зависимости от способа грамматического разбора изменяется смысл предложения. Этот пример показывает то важное для формальных языков обстоятельство, что грамматический разбор исходного текста программы, есть важнейший шаг на пути компиляции программы . 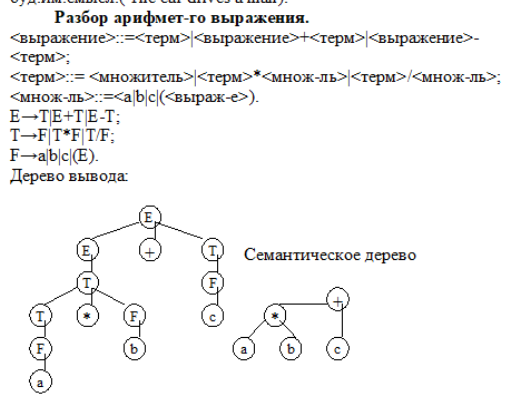 Контекстная грамматика. Контекстно-свободная грамматика. Прописные буквы нетерминальные символы языка, строчные-терминальные, 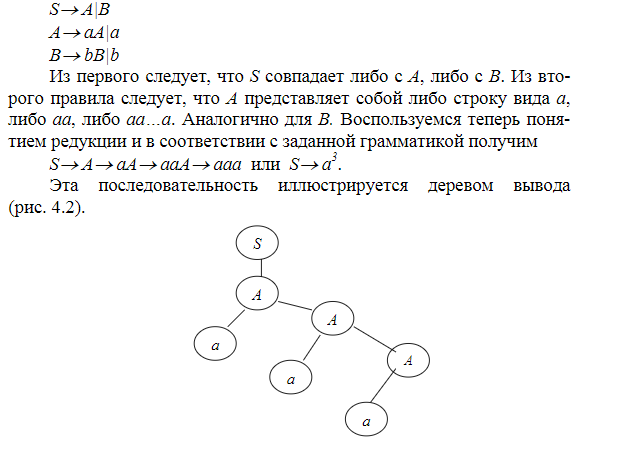 Всякое дерево вывода начинается с корня S в соответствии с правилами вывода происходит дв-е по ветвям строющегося дерева до тех пор, пока все нетерм-е символы не буд.раскрыты ч/з терм-е. Контексная гр-ка(К/Г) – это совокуп-ть 4х объектов: G=(N,T,P,S), где N-конеч.мн-во нетерм.симв-в, T-кон.мн-во терм.симв, P-кон.мн-во продук-й вида α→β, где a- строка в левой части продукции, такая что α 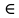 (NUT)+-без пустой строки, β- строка в правой части, β (NUT)+-без пустой строки, β- строка в правой части, β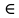 (NUT)*т.е. м/о получить и пуст.строку, (NUT)*т.е. м/о получить и пуст.строку,S-начальный символ. Если строка α 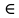 (NUT)* за 1н или неск-ко шагов выводится из начального сим-ла S (NUT)* за 1н или неск-ко шагов выводится из начального сим-ла S формой К/Г-ки G. ( 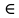 Т* | Т* |Если две грамматики порождают один и тот же язык, те В форм. языках чаще всего в левой части продукции испол-ся 1н нетерм-й симв-л, кот-й явл-ся единс-м симв-м слева. К/Г-ка, удовл-щая этому требованию наз-ся КС/Г-ой. Строгое опред-е КС/Г-ки : гр-ка G=(N,T,P,S), в кот-й мн-во P содержит продук-ии вида α→β, где α 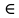 N, β N, β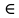 (NUT)*. Термин КС возник, т.к. люб. симв-л α (NUT)*. Термин КС возник, т.к. люб. симв-л α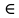 N в сентанц. форме гр-ки G м.б.раскрыт согласно продукции из α→β,независимо от того, какими строками он окружен внутри самой сент. формы. N в сентанц. форме гр-ки G м.б.раскрыт согласно продукции из α→β,независимо от того, какими строками он окружен внутри самой сент. формы.КС/Г-ку м/о представить виде дерева вывода. Корнем кот-го явл-ся нач.символ S, строка терм-х симв-в, или сентенция – последов-ть висящих вершин, читаемых в порядке слева направа. Промеж-е узлы дерева– нетерм-е верш-ны. Если для люб. строки х 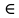 L(G) все возможные схемы вывода имеют одно и тоже дерево вывода, то гр-ка наз. однозначная КС/Г-кой. (S→AB; A→aA|a; B→bB|b –строка а3b2). Если одной и той же строке соотв-т разл. деревья, то гр-ка наз. неоднозна-й (S→SbS|ScS|a-строка abaca). В дан.опред-ии КС/Г-ки ее продукции им.вид: α→β, где α L(G) все возможные схемы вывода имеют одно и тоже дерево вывода, то гр-ка наз. однозначная КС/Г-кой. (S→AB; A→aA|a; B→bB|b –строка а3b2). Если одной и той же строке соотв-т разл. деревья, то гр-ка наз. неоднозна-й (S→SbS|ScS|a-строка abaca). В дан.опред-ии КС/Г-ки ее продукции им.вид: α→β, где α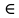 N, β N, β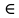 (NUT)*. Значит корректна запись А→ε, где ε-терм. символ. (NUT)*. Значит корректна запись А→ε, где ε-терм. символ.Гр-ка не им-щая ε-прод-ции наз. ε-своб-й. Было бы идеально раб-ть т/о с ε-своб-ми гр-ми. Для преобр-ия гр-ки G в гр-ку G’, кот-я ε-своб-на н/о: 1. объединить все имеющиеся в Р ε-продукции в мн-во Р’. 2. все нетерм.сим-лы, т.ч. 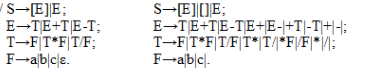 Регулярные грамматики и конечный автомат.   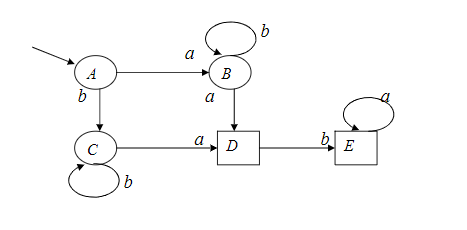 ДЕТЕРМИНИРОВАННЫЙ АВТОМАТ. Для этого графа, функция t не полная, тк не определена на парах (D,a) и (E,b) 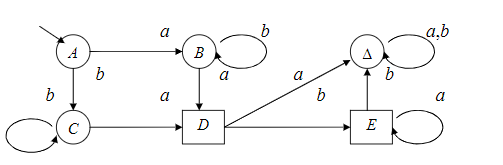 Если t неполная, можно добавить еще одно фиктивное состояние   Эквивалентность автоматов. Для каж-го конеч.ав-та сущ-т бескон-е кол-во др-х конеч-х ав-в, кот-е распоз-т те же цепочки. Но сущ-т единс-й кон.ав-т, кол-во состояний кот-го минимально. Два состояния наз.эквивалентными, если они одинаково реагируют на все продолжения входных цепочек. Состояние S конечного распознователя М экв-но сост-ю t кон-го распоз-ля N тогда и т/о тогда, когда авт-т М, начав работу в сост-ии S б/т допускать те же цепочки, что и ав-т N, начав работу в сост-ии t. Из опред-ия эквив-х сост-й м/о дать опред-е экв-х авт-в: Авт-ты М и N экв-ны,тогда и т/о тогда, когда экв-ны их начальные состояния. Проверка экв-ти сост-й основывается на: 1.условие подобия, т.е.сост-я S и t должны 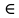 или к допуск-м, или к отвергающим. или к допуск-м, или к отвергающим.2.условие приемственности, т.е.для всех входных сим-в, сост-я S и t должны переходить в др-е эквивал-е сост-ия, т.е.их приемники д.б.эквив-ными. (метод№1):метод таблиц экв-х сост-й. 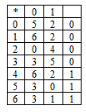 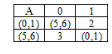 1.строется таблица эквив-сти сост-й(А), первыми запис-ся два начал-х сост-я, кот-е подверг-ся анализу. 2.выбирается строка в дан.таблице, ячейки кот-й еще не заполнены и проверяется подобны ли состояния, кот-ми она помечена. Если сост-я не подобны, то два исходных сост-я не эквив-ны и процесс завершен, если подобны, то вычисляется рез-т применения каж-го вход-го сим-ла к этой паре сост-й и записыв-сяполученные пары сост-й. 3. если пара разл-х сост-й(получ-х на 2 шаге) еще не использ-сь как метка, то она перепис-ся на новую строку. 4. если таблица завершена выписыв-ся все состояния, поражденные в ходе проверки,кот.б/т экв-ми сост-ми. В нашем пр-ре 0 |
Сущ-т еще 1н метод №2:метод разбиения на непересекающиеся подмн-ва.
1.все мн-во сос-й разбив-ся на 2 блока, 1н блок содержит т/о отверг-е, др-й т/о доп-щие сост-ия. Ни одно сост-е 1-го блока не м.б.экв-но как.либо состоянию из 2-го блока. (см табл.*) Р1=({0,1,2,3},{4,5,6})
2.расс-м переходы в 1м блоке под возд-ем 0. из сост-й 0и1 переход в 5и6- доп-щие сост-ия, из 2и3 переход в 0и3-отверг-е сост-я, значит Р2=({0,1},{2,3},{4},{5,6}).
3.расс-е поведение блока {2,3} если на входе дей-т серия сим-в 0: они не экв-ны, Р3=({0,1},{2},{3},{4},{5,6}).
4.дальнейшие попытки разбить блок ={0,1}и {5,6}ничего не дают, значит 0
