ВОПРОСЫ К ЭКЗАМЕНУ ПО ТЕОРИИ АВТОМАТОВ. Вопросы к экзамену Строки. Префиксы, суффиксы, подстроки. Формальные языки
 Скачать 3.16 Mb. Скачать 3.16 Mb.
|
|
Теорема о структурной полноте В.М.Глушкова. 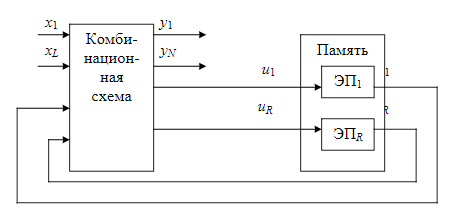 Автомат представляется как совокупность 2 частей- памяти и комбинационной схемы. ЭП-iый элемент памяти, x- входные каналы автомата, y- выходные каналы автомата, u – ф-я возбуждения памяти автомата, v- обратной связи автомата. Теорема о структурной полноте Глушкова: для того, чтобы система элементарных автоматов была структурно полной необходимо и достаточно, чтобы она содержала хотя бы один автомат мура с полной системой переходов и полной системой выходов, а также функционально полную систему логических элементов Автомат мура обладает полной системой переходов, если для любой пары состояний (ai,aj) найдётся входной сигнал, переводящий один элемент пары в другой, включая случай, когда i=j. Автомат мура обладает полной системой выходов, если каждое состояние автомата отмечено выходным сигналом, отличным от сигналов, отмечающих остальные состояния. Элементарным автоматом называется автомат с двумя состояниями. Логический элемент - интегральная схема реализующая булеву функцию. . Канонический метод структурного синтеза автоматов (Модель дискретного преобразователя В.М.Глушкова) Комбинационная схема (КС) может иметь несколько выходов. При каноническом методе предполагается, что каждая выходная функция реализуется своей схемой, совокупность которых и даёт требуемую КС. Поэтому синтез сложной КС с n выходами заменяется синтезом n схем с одним выходом. Согласно каноническому методу синтез КС включает в себя ряд этапов. 1. Подлежащая реализации булева функция (или её отрицание) представляется в виде СДНФ. 2. С использованием методов минимизации определяется минимальная ДНФ (МДНФ) или минимальная КНФ (МКНФ). Из полученных двух минимальных форм выбирается более простая. 3. Булеву функцию в минимальной форме согласно п.2 представляют в заданном (или выбранном разработчиком) базисе . 4. По представлению функции в заданном базисе строят комбинационную схему. Необходимо отметить, что подлежащая реализации булева функция F(X1,X2,...,Xm) может быть задана не на всех возможных наборах аргументов X1, X2, ..., Xm. На тех наборах, где функция неопределенна, её доопределяют так, чтобы в результате минимизации получить более простую МДНФ или МКНФ. При этом упростится и сама КС. Кроме того, довольно часто с целью получения ещё более простого представления функции МДНФ, полученная в п.2, представляется в так называемой скобочной форме, т.е. выносятся за скобки общие части импликант МДНФ. Авт-т любой сложности представл в виде структуры,сост из 2-х частей:  В схеме след обозначения: X1-XL – множ-во входных сигналов структурного авт-та Y1-YN – множ-во выходных сигналов U1-UR – множ-во сигналов возбуждения ЭП V1-VR – множ-во сигналов обратной связи Теорема Глушкова (Система элементарных автоматов явл структурно полной тогда и только тогда,когда содержит: 1)авт-ты Мура,облад полнотой переходов и выходов. 2).комбинацион схему,постороенную на функционал полной системе логических элементов. В этом случае задача структурного синтеза произвольных автоматов сводится к задаче структурного синтеза комбинационных схем). В соответ-ии с теоремой Глушкова задача синтеза структ авт-та сост в построении комбинац части.Математически это записыв-ся так: y1=y1(x1,x2,…,xL,V1,V2,…,VR)… yN=yN(x1,x2,…,xL,V1,V2,…VR) U1=U1(x1,x2,…,xL,V1,V2,…VR)… UR=UR(x1,x2,…,xL,V1,V2,…VR). Т.о.,задача синтеза структурного авт-та сводится к составлению и решению этой сист логических уравнений. СДНФ( по 1) и СКНФ( по 0)  Минтермы- произведение Макстермы- сумма   Синтез автомата на D- и RS-триггерах.  СНФ в базисе «Стрелка Пирса» и «Штрих Шеффера»   отрицаем, где 0  Для обозначения логических принципиальных схемах используют спец изображения  Графический метод структурного синтеза автоматов. Этапы графического метода синтеза структурного автомата:  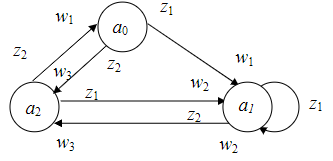 Определение структуры структурного автомата. 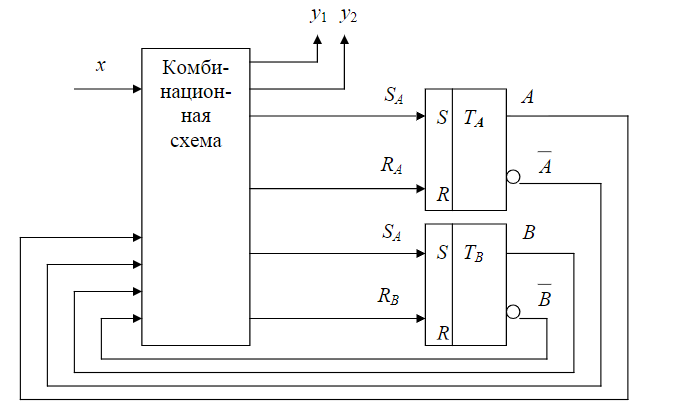 Находим количество элементов памяти Кодируем входные и выходные сигналы.  Структурный автомат представляем обобщенной схемой. 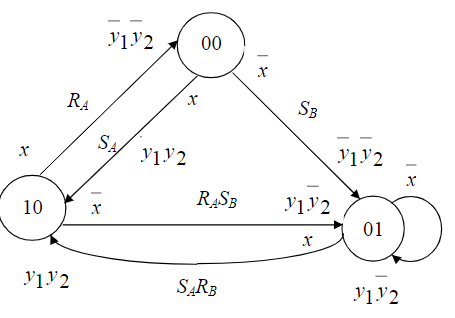 Составление уравнений выходных функций. Представляем закодированный граф абстрактного автомата, то есть вместо состояний автомата указываются соответствующие кодовые комбинации, а входные сигналы указываются на переходах своими логическими кодовыми комбинациями. Логические кодовые комбинации выходных сигналов 1 рода записываются на переходах, а сигналы 2 рода записываются как метки состояний (или внутри вершины графа). Причем для выходных функций следует указывать только те значения функций, которые принимают истинные значения, по которым составляются уравнения выходов.  Составление уравнений функций возбуждения. На закодированном графе на дугах перехода указываем функции возбуждения, которые соответствуют переключению триггеров, причем следует указывать только те значения функций, которые принимают истинные значения, по которым составляются уравнения функций возбуждения. Уравнения функций возбуждения и выходов минимизируются (по картам Карно, например) и по ним строится схема в заданном функционально - логическом базисе ({И, ИЛИ, НЕ}, {И-НЕ}, {ИЛИ-НЕ} ). Свойства функций «Исключающее ИЛИ», «Импликция от У к Х».    Синтез комбинационных схем на ПЗУ. ПЗУ представляет собой память, программируемую 1 раз(например, при изготовлении). Записанная информация сохраняется в течение всего времени эксплуатации. ПЗУ имеет k адресных входов и n выходов.->Можно записать 2^k n-разрядных двоичных слов. Большое распространение для синтеза комб. сх. получили программируемые логические матрицы. ПЛМ представляют собой множество связанных м/у собой определенным образом дизъюнктеров и конъюнктеров. Перед программированием имеет вид как:  x- электрические соединения, некот-е при програм-е ПЛМ уничтожаются. НА выходе в зависимости от уничтожения или сохранения x связи, можно получить как прямое, так и инверсное значение ф-ции. Лог. характ-й ПЛМ (n,p,k) n- число входов, p- число выходов, k- число конъюнктеров.n,p- столбцы, k-строки. Площадь N=(n+p)*k. Структурно ПЛМ - 2 матрицы M1(реализует k всевозможных конъюнкции от n переменных) и M2(p всевозможных дизъюнкций от k переменных) 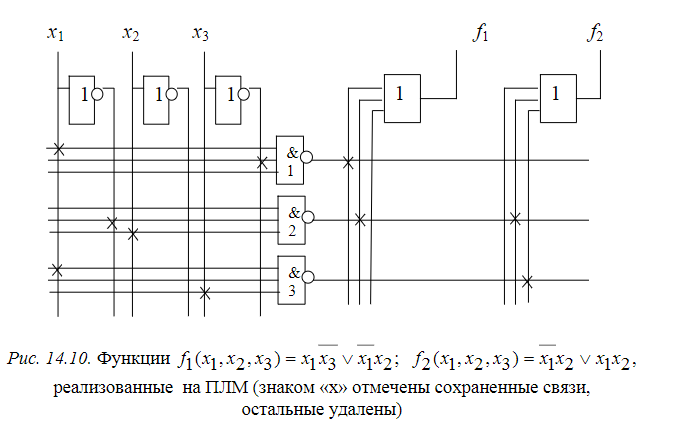 2 задачи синтеза: реализовать схему, минимизируя площадь ПЛМ реализовать схему на минимальном числе ПЛН с известными параметрами(n,p,k)  Свойства функций «Штрих Шеффера», «Стрелка Пирса».   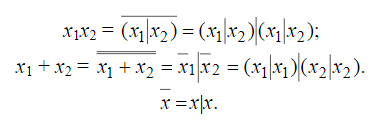 Дешифратор в цепи ОС структурного автомата. Дешифраторы и шифраторы (также, как и элементы И,ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ) являются комбинационными элементами: потенциалы на их выходах зависят от сиюминутного состояния входов, с их изменением меняется и ситуация на выходах; такие элементы не сохраняют предыдущее состояние после смены потенциалов на входах, т.е. не обладают памятью. Дешифраторы могут быть полными и неполными. Полные дешифраторы реагируют на все входные коды, неполные – на коды, величина которых не превосходит некоторого заранее установленного значения. Выходы дешифраторов могут быть прямыми и инверсными. Дешифратор называется полным, если он имеет количество выходов m, связанных с количеством разрядов n входного двоичного числа следующим соотношением: m=2n Дешифратор, у которого при n входах число выходов меньше 2n (m<2n), называется неполным. 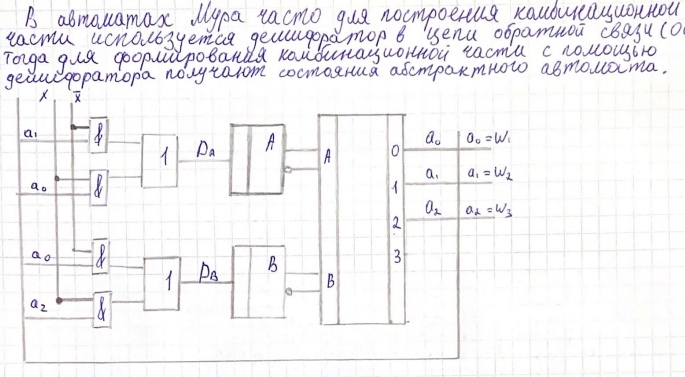 Классы логических функций. Базис - полная система функций алгебры логики, с помощью которой любая функция может быть представлена суперпозицией исходных функций. Базис 1. И, ИЛИ, НЕ (булевый). Базис 2. И, НЕ. Базис 3. ИЛИ, НЕ. Базис 4. Штрих Шеффера. Базис 5. Стрелка Пирса. Из перечисления следует, что базисы могут быть избыточными(1) или минимальными(остальные). Так, из первого базиса может быть удалена функция “И” или “ИЛИ”, тогда будет осуществлен переход к базисам 3 или 2 соответственно. Для того чтобы ответить на вопрос, какие функции могут образовывать базис, необходимо установить некоторые свойства логических функций, определяемые их принадлежностью к классам функций. Класс линейных функций (КЛ). Логическая функция называется линейной, если она представляется полиномом первой степени Количество линейных функций равно 2n+1. Например, для n=2 количество линейных функций равно 8:  Класс функций, сохраняющих нуль(К0). Если функция на нулевом наборе переменных равна нулю, говорят, что функция сохраняет нуль: f(0, 0, …, 0) = 0. Класс функций, сохраняющих единицу(К1). Если функция на единичном наборе переменных равна единице, говорят, что функция сохраняет единицу: f(1, 1, …, 1) = 0. Класс монотонных функций(Км). Функция алгебры логики является монотонной, если при любом возрастании номера набора переменных значения этой функции не убывают. Класс самодвойственных функций(Кс). Функция алгебры логики является самодвойственной, если выполняется равенство: Названные классы функций обладают замечательным свойством: любая функция, полученная с помощью суперпозиции и подстановки из функций одного класса, будет принадлежать этому же классу. Определим принадлежность функций, указанных в табл. 12.8, описанным классам. Определяется следующие 5 классов: 0 – класс: Функции, которые сохраняют нулевое значение на нулевом наборе терминов 1 – класс: Все функции, которые имеют значение 1 на единичном значении термов, то есть 2 – класс: Класс линейных функции – все функции, у которых в полиномиальном представлении нет слагаемого . 3 – класс: Класс самодвойственных функций – функции, для которых выражается соотношение: 4 – класс: Класс монотонных функций – функции, для которых выражается неравенство: Теорема Поста-Яблонского. Теорема Поста-Яблонского определяет необходимые и доста- точные условия для получения базиса. Чтобы система логических функций была полной (базисом), необходимо и достаточно, чтобы она содержала хотя бы одну функцию: - не сохраняющую нуль; - не сохраняющую единицу; - не являющуюся линейной; - не являющуюся монотонной; - не являющуюся самодвойственной.  Как видно из таблицы, условиям теоремы Поста-Яблонского удовлетворяют только две функции: f8 - Стрелка Пирса и f14 Штрих Шеффера, которые обладают функциональной полнотой. Комбинации функций f11 и f12 или f4 и f9, а также некоторых других также образуют базисы. Наибольшее применение нашли описанные выше 5 базисов. Для обозначения функций на логических принципиальных схемах используют специальные изображения:  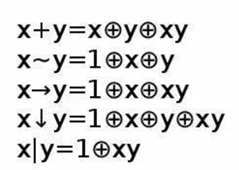 Состязания (гонки) в автоматах. Мат. аппарат исп-й при синтезе автоматов, строится на основе булевой алгебры, в к-й не учит. реальное время срабатывания лог. элементов.Однако реальные процессы переключения элементов, реализующих логические зависимости, происходит во времени с конечными задержками,если при синтезе автомата не учитывать фактор времени, то работа автомата может быть неправильной. Состязания или гонки - ситуация, при которых может появится риск сбоя. Критические состязания - состязания, приводящие автомат в устойчивые состояния, не предусмотренные законом функционирования. Переключение автомата в следующее состояние производится сигналами возбуждения, вырабатываемыми в комбинационной части автомата и поступающими на входы триггеров запоминающей части. Если при переходе автомата из состояния аi в состояние аj несколько триггеров должны изменить свое состояние, то из-за различия моментах срабатывания могут начаться состязания. Тот триггер, который выиграет состязания, может через цепь обратной связи при определенных условиях изменить сигналы на входах остальных триггеров раньше, чем те изменят свое состояние. В результате гонок триггеры могут перейти в состояние, не соответствующее закону функционирования автомата, т.е. состояния будут критическими. Для искл-я опасных состяназний исп. спец. противогоночное кодирование либо аппаратные средства.К ним относят:1)выравнивание задержек по различным цепям распространения сигналов;2)импульсную синхронизацию; 3)двухступенчатую (двойную) память;4)апериодические схемы |
