Лекции По Основам Светотехники (Шашлов А. Б.). Лекции По Основам Светотехники (Шашлов А. Б. Вопросы к экзамену. Вопрос 1

• Название: Вопросы к экзамену. Вопрос 1
• Анкор: Лекции По Основам Светотехники (Шашлов А. Б.).doc
• Дата: 18.05.2017
• Размер: 3.97 Mb.
• Имя файла: Лекции По Основам Светотехники (Шашлов А. Б.).doc
• Тип: Вопросы к экзамену; #7863
• Категория: Физика
• страница: 3 из 6

Вопрос №9

44. Закон Бугера - Ламберта- Бера. 45. Величины, связываемые законом. 46. Смысл показателей К и Х. 47. Аддитивность оптических плотностей. 48. Отклонения от закона. 49. Закон Ламберта. 50. Индикатрисы светорассеяния, мутность сред. 51. Типы светорассеяния.
44. Закон Бугера - Ламберта- Бера.

Для монохроматического излучения.

1) Бугер и Ламберт открыли закон, связывающий поглощение монохроматического излучения гомогенной средой с толщиной слоя этой среды. Ламберт предложил для закона математическое выражение:



Бэр установил, что при поглощении монохроматических излучений разбавленными растворами вещества в прозрачном растворителе коэффициент поглощения . Зависимость

- объединенный закон Бугера-Ламберта-Бэра

2) На практике закон Бугера-Ламберта и объединенный закон Бугера-Ламберта-Бэра записывают так:



т.е. переходят от основания натуральных логарифмов "е" к основанию "10", кроме того, обычно опускают индекс "".

3) логарифмическое выражение закона Бугера-Ламберта-Бэра:



где - ( )- удельный показатель поглощения. Это постоянная, не зависящая от толщины и концентрации светопоглощающего вещества, но зависящая от его природы и длины волны излучения. С – ()- концентрация светопоглощающего вещества, l- (м)- толщина.

Для сложного излучения. Для сложного излучения (дневной свет, свет реальных источников) выражение для Ф/Ф0 имеет более сложный вид, чем для монохроматического излучения: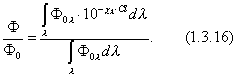


для нейтрально-серых оптических сред можно перейти от потоков излучения Ф к световым потокам F. закона Бугера-Ламберта-Бэра в виде


Закон применяют когда:

1) исключено отражение излучения (= 0) от поверхности материала или слоя вещества. Если , входящий в материал поток равен не

2) Среда гомогенная . Если оптическая среда мутная, т.е. гетерогенная, она рассеивает часть света. Для таких сред закон не соблюдается.

45. Величины, связываемые законом.

В Законе связываются поглощение монохроматического излучения гомогенной средой с толщиной слоя этой среды

- Закон Бугера - Ламберта –Бэра. Законом связываются - поток монохроматического излучения, падающий в виде пучка параллельных лучей на слой гомогенной поглощающей среды перпендикулярно ее поверхности; - поток излучения, прошедший через слой; - коэффициент поглощения, не зависящий от мощности излучения , но зависящий от природы вещества, составляющего слой, и длины волны падающего излучения. При поглощении монохроматических излучений разбавленными растворами вещества в прозрачном растворителе коэффициент поглощения К в формуле Бугера -Ламберта пропорционален концентрации светопоглощающего вещества .

В логарифмическом выражении закона Бугера-Ламберта-Бэра:

связываются величины

- удельный показатель поглощения (м²/г). Это постоянная, не зависящая от толщины и концентрации светопоглощающего вещества, но зависящая от его природы и длины волны излучения, концентрации вещества С (г/м³) и толщина слоя вещества l (м)

46. Смысл показателей χ ,К.

логарифмическое выражение закона Бугера-Ламберта-Бэра:



где - удельный показатель поглощения. Это постоянная, не зависящая от толщины и концентрации светопоглощающего вещества, но зависящая от его природы и длины волны излучения. Ее единица измерения определяется единицами измерения концентрации вещества С и толщины слоя вещества l. Если С выражена в , а l в метрах, то имеет размерность .

Из формулы , следует, что оптическая плотность зависит от природы светопоглощающего вещества и пропорциональна поверхностной концентрации вещества .

Бэром было установлено, что при поглощении монохроматических излучений разбавленными растворами вещества в прозрачном растворителе коэффициент поглощения К в формуле Бугера-Ламберта пропорционален концентрации светопоглощающего вещества . Зависимость



Называется объединенным законом Бугера-Ламберта-Бэра

47. Аддитивность оптических плотностей.

Если в материале имеется несколько (например, три) светопоглощающих вещества с концентрациями и удельными показателями поглощения , то для расчетов можно использовать выражения

- закон Бугера- Ламберта- Бэра

ЕСЛИ материал слоистый и слои различаются по всем параметрам (, С,l ), то для него справедливо выражение



((1.3.17)-( 1.3.19)) справедливы для двух случаев: а) любая среда в сочетании с монохроматическим излучением, б) любое видимое излучение в сочетании с нейтрально-серой средой.

Из выражения 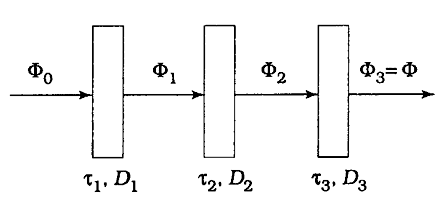следует аддитивность оптических плотностей: при сложении оптических сред их оптические плотности складываются см. рис.:




Перейдя от "Ф/Ф0" к "", можно записать: .Отсюда

т.е. при сложении оптических сред их коэффициенты пропускания перемножаются.
49. Закон Ламберта.

Это закон, связывающий поглощение монохроматического излучения гомогенной средой с толщиной слоя этой среды. Ламберт предложил для закона математическое выражение:



где - поток монохроматического излучения, падающий в виде пучка параллельных лучей на слой гомогенной поглощающей среды перпендикулярно ее поверхности; - поток излучения, прошедший через слой; - коэффициент поглощения, не зависящий от мощности излучения, но зависящий от природы вещества, составляющего слой, и длины волны падающего излучения. Закон был выведен для условия , Когда отсутствует отражение излучения от поверхности слоя вещества.
50. Индикатрисы светорассеяния, мутность сред.

1. Отраженный и пропущенный средой свет распространяется в пространстве во всех направлениях. Такое явление называется диффузным рассеянием света.

И. Ламбертом было установлено, что, если поверхность полностью рассеивает свет, ее яркости во всех направлениях одинаковы и не зависят от угла падения светового пучка на поверхность, т.е. В() = const, где В - яркость в направлении, создающем с нормалью N угол .

При В() = const сила света, отражаемого поверхностью, будет различной в разных направлениях. Это видно из выражения, связывающего яркость В с силой света I: , где dQ - площадь малого участка рассеивающей поверхности. Для направления, совпадающего с нормалью

Заменив в формуле для I через , получим математическое выражение закона Ламберта:



Распределение яркости и силы света, отраженного от малого участка рассеивающей поверхности, можно выразить в виде векторных диаграмм 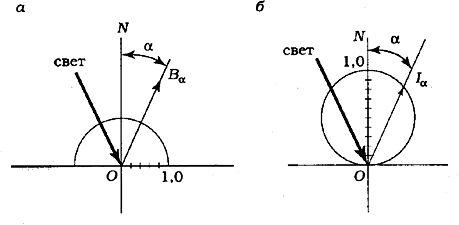, построенных в полярных координатах. Огибающая этих векторов представляет собой индикатрису рассеяния. Строятся они в относительных величинах. На рис.



показаны индикатриса яркости (а) и индикатриса силы света (б) для идеального диффузора. Индикатриса яркости имеет форму половины окружности с центром в точке падения света О. Индикатриса силы света имеет форму окружности, касающейся поверхности в точке падения света О.

Большинство окружающих нас физических тел частично рассеивают свет. Поэтому их яркости в разных направлениях будут различными и форма индикатрисы будет зависеть от угла падения света на поверхность тела (рис.), б (i1 = 0, i2 > 0, i3 > i2)).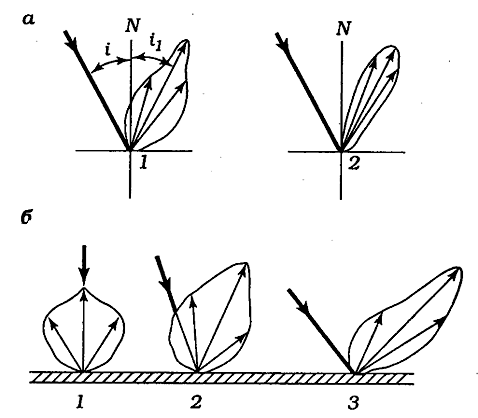



2. мутность сред.

Мутные среды

Известны три типа оптических систем, относящихся к мутным средам: системы с оптически тонким, средним (промежуточным) и толстым слоем.

Оптически тонкий слой. Рассеянный свет, наблюдаемый в оптически тонких системах, отражается лишь один раз; при этом большая часть нерассеянного света проходит сквозь образец [6]. Примером таких систем являются прозрачные красители, наносимые на текстильный материал.

Оптически средний слой. Большая часть рассеянного света многократно рассеивается, однако, часть света все же проходит сквозь образец [6]. Типичным примером такой среды является окрашенный полистирол. Большинство систем, которые относят к категории оптически тонких или оптически толстых сред, на самом деле относятся к оптически промежуточному слою. Полиграфические офсетные краски считаются оптически тонким слоем, а краски для трафаретной печати — оптически толстым. Однако и ту, и другую краску следует все же отнести к среднему слою.

Оптически толстый слой. Весь свет многократно отражается [6]. Примером оптически толстого слоя являются непрозрачные покрытия, в которых диоксид титана смешан с другими рассеивающими пигментами.

51. Типы светорассеяния.

Типы светорассеяния

1)угол падения равен углу отражения – зеркальное



2) диффузное



3) смешанное

Отражение


4) направленное



Вопрос № 10.

52. Закон Вебера-Фехнера. 53. Световая величина, называемая светлотой 54 Порог различения 55. Метод измерения светлоты в порогах

56. Связь светлоты с яркостью: разностный и дифференциальный пороги

57 Формула, выражающая закон Вебера-Фехнера.

58 Формула, выражающая закон Вебера-Фехнера. 59. Связь светлоты с оптической плотностью.
52. Закон Вебера-Фехнера

Закон Вебера — Фехнера — эмпирический психофизиологический закон, заключающийся в том, что приращение светлоты пропорционально приращению логарифма яркости.

53. Световая величина, называемая светлотой

Свеетлота – субъективная оценка, связанная с ощущением, поэтому разность светлот трудно поддается точному количественному измерению. В качестве единицы измерения разности светлот был предложен порог различения светлоты dW. Это минимальная разница, замечаемая глазом. Любая конечная разность светлот ΔW выражается числом порогов различения светлоты.

Светлота объекта определяется его яркостью, поэтому для удобства измерения полезно связать между собой порог различения и разницу яркостей, ему соответствующему.

54 Порог различения

В качестве единицы измерения разности светлот был предложен порог различения светлоты dW. Это минимальная разница, замечаемая глазом. Любая конечная разность светлот ΔW выражается числом порогов различения светлоты. Порог различения был определен в специальных колориметрических условиях, так как он неодинаков у разных людей и зависит от условий рассматривания.


55. Метод измерения светлоты в порогах

Схема прибора для оценки световых величин методом пороговых приращений.



Эксперимент был очень прост. На стороны белой призмы направлялось два потока света. Эти потоки можно было регулировать, например, по яркости, изменяя диафрагму, как в фотоаппарате. Наблюдатель рассматривал призму через окуляр, так что ее грани казались двумя прямоугольниками, не имеющими четкой границы. Если поля освещались по-разному, то одно, естественно, казалось светлее, а другое темнее. (Вот и еще одно понятие - светлота ). Наблюдатель регулировочными ручками уравнивал поля по светлоте. Затем находил, насколько больше яркость одного из полей, если оно едва заметно светлее другого. Оказалось, что в физическом измерении эта величина всегда одна и та же. Ее назвали порогом . Если измерить увеличение светлот в порогах, то оно будет пропорционально десятичному логарифму увеличения яркостей (или соответствующему уменьшению другой логарифмической величины, оптических плотностей ).

56. Связь светлоты с яркостью: разностный и дифференциальный пороги

Сопоставим изменение светлоты с изменением яркости, Фехнер установил, что порогу различения светлоты ΔWпор соответствует постоянное относительное изменение яркости

ΔB/B=Ψ

Названное им пороговым контрастом или дифференциальным порогом. Им было установлено, что в диапазоне яркостей 1-1000 кд/м^2 порогу различения соответствует дифференциальный порог около 2%.
57 Формула, выражающая закон Вебера-Фехнера

Приращение светлоты пропорционально приращению логарифма яркости

ΔW=k * Δ lg B

W- светлота

k – коэффициент , равный числу порогов различения, соотвутствующему десятикратному увеличению яркости

В – яркость
58 Формула, выражающая закон Вебера-Фехнера.

, где k- коэффициент пропорциональности. Эта формула является математическим выражением закона Вебера-Фехнера, утверждающего, что приращение светлоты пропорционально приращению логарифма яркости.
59. Связь светлоты с оптической плотностью.

Связь между оптической плотностью и светлотой описывается законом Вебера-Фехнера. Согласно этому закону, контраст изображения, равный разности светлот , определяется разностью оптических плотностей участков изображения.

, где k-коэффициент пропорциональности


Вопрос № 11

60 Оптическая плотность, определение термина.

61 Связь оптической плотности с концентрацией светопоглощающего вещества и видимыми свойствами изображения

62 Показательная и логарифмическая формы закона Бугера-Ламбера-Бера.

63 Принципы измерения оптической плотности.

64 Типы оптических плотностей (регулярная и диффузная).
.

60 Оптическая плотность, определение термина.

Оптическая плотность-степень пропускания света для прозрачных объектов и отражения для непрозрачных.

61 Связь оптической плотности с концентрацией светопоглощающего вещества и видимыми свойствами изображения. , где -удельный показатель поглощения, l-толщина слоя вещества, С-концентрация вещества.

62 Показательная и логарифмическая формы закона Бугера-Ламбера-Бера.

Показательная форма-,где -удельный показатель поглощения, l-толщина слоя вещества, С-концентрация вещества. Логарифмическая форма закона-


63 Принципы измерения оптической плотности.

Оптические плотности измеряют на приборах, называемых денситометрами. Современные денситометры имею набор различных светофильтров, позволяющих производить измерения в различных условиях. Черно-белые изображения и нейтрально-серые измеряются с использованием светофильтра видности.