Коллоквиум. Вопросы к коллоквиуму Материальная точка
 Скачать 2.08 Mb.
|
|
Вопросы к коллоквиуму 1.Материальная точка – тело, размерами которого можно пренебречь в условиях данной задачи. Поступательное движение – движение тела, при котором все точки тела движутся одинаково. Система отсчёта – система, которая состоит из тела отсчёта, связанная с ним системой координат и часов. 2. Траектория — это линия, вдоль которой движется тело. На рис. 1 траекторией точки  является синяя дуга, которую описывает в пространстве конец радиус-вектора  .Путь — это длина участка траектории, пройденного телом за данный промежуток времени. Перемещение — это вектор, соединяющий начальное и конечное положение тела. Предположим, что тело начало движение в точке  и закончило движение в точке 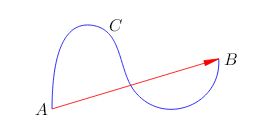 (рис. 2). Тогда путь, пройденный телом, это длина траектории  . Перемещение тела — это вектор  . Радиус-вектор {\displaystyle \mathbf {r} }— вектор, задающий положение точки в пространстве (например, евклидовом) относительно некоторой заранее фиксированной точки, называемой началом координат. Понятие используется в математике (геометрии) и физике. В кинематике изменение радиус-вектора со временем, то есть функция {\displaystyle {\vec {r}}(t)}  , определяет движение материальной точки. Если указанная функция известна, на её основе могут быть вычислены скорость и ускорение:{\displaystyle {\vec {v}}(t)={\frac {{\mbox{d}}{\vec {r}}(t)}{{\mbox{d}}t}}={\dot {\vec {r}}}(t)} {\displaystyle {\vec {a}}(t)={\frac {{\mbox{d}}^{2}{\vec {r}}(t)}{{\mbox{d}}t^{2}}}={\ddot {\vec {r}}}(t)} , 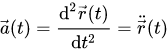 где точка сверху обозначает дифференцирование по времени, а две точки — двукратное дифференцирование. В таком виде запись применима к системе координат любого типа. Но переход к трём координатам декартовой, цилиндрической и сферической систем осуществляется по-разному. 3. Мгновенная скорость. Мгновенное ускорение (тангенциальное, нормальное, полное) Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, которая равна пределу, к которому стремится среднее ускорение при стремлении промежутка времени к 0. Другими словами – это ускорение, развиваемое телом за очень маленький отрезок времени: 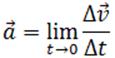 .Ускорение имеет такое же направление, как и изменение скорости Δ  в крайне маленьких промежутках времени, за которые скорость изменяется. Вектор ускорения можно задать при помощи проекций на соответствующие оси координат в заданной системе отсчета (проекциями аХ, aY, aZ).При ускоренном прямолинейном движении скорость тела увеличивается по модулю, т.е. v2 > v1, а вектор ускорения имеет такое же направление, как и у вектора скорости 2.Если скорость тела по модулю уменьшается (v2 < v1), значит, у вектора ускорения направление противоположно направлению вектора скорости 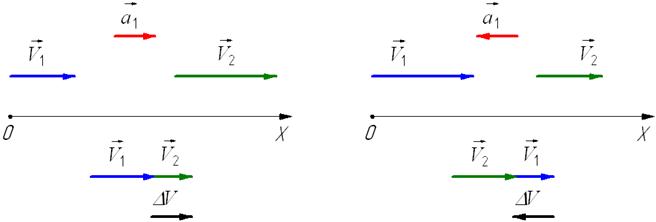2. Другими словами, в таком случае наблюдаем замедление движения (ускорение отрицательно, а < 0). На рисунке ниже изображено направление векторов ускорения при прямолинейном движении тела для случая ускорения и замедления. Если происходит движение по криволинейной траектории, то изменяется модуль и направление скорости. Значит, вектор ускорения изображают в виде 2х составляющих. Тангенциальное ускорение.Тангенциальным (касательным) ускорением называют ту составляющую вектора ускорения, которая направлена по касательной к траектории в данной точке траектории движения. Тангенциальное ускорение описывает степень изменения скорости по модулю при совершении криволинейного движения. 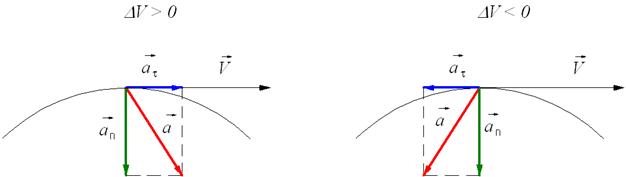 У вектора тангенциального ускорения  τ (см. рис. выше) направление такое же, как и у линейной скорости либо противоположно ему. Т.е. вектор тангенциального ускорения находится в одной оси с касательной окружности, являющейся траекторией движения тела.Нормальное ускорение.Нормальным ускорением является та часть вектора ускорения, которая направлена по нормали к траектории движения в заданной точке на траектории движения тела. Т.е. вектор нормального ускорения расположен перпендикулярно к линейной скорости движения (см. рис. выше). Нормальное ускорение описывает степень изменения скорости по направлению и обозначается как n. Вектор нормального ускорения направлен по радиусу кривизны траектории.Полное ускорение.Полное ускорение при криволинейном движении составляется из тангенциального и нормального ускорений по правилу сложения векторов и вычисляется при помощи формулы: 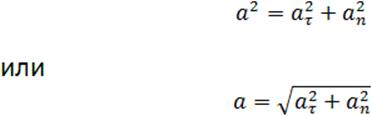 (по теореме Пифагора для прямоугольного прямоугольника). При помощи правила сложения векторов вычисляем и направление полного ускорения: = τ + n.4. Прямолинейное равнопеременное движение — движение тела вдоль прямой, характеризующееся постоянным по модулю и направлению линейным ускорением. Траектория такого движения — прямая, поэтому в задачах равнозначными являются понятия пути и модуля перемещения. Такое движение может быть описано несколькими соотношениями: вектор скорости тела при равнопеременном движении  (1)где  — вектор конечной скорости движения — вектор начальной скорости движения — вектор ускорения — время движениявектор перемещения тела при равнопеременном движении  (2)где Однако это векторные уравнения, с которыми работать достаточно сложно, а иногда, просто не хочется. Попробуем, анализируя условия задачи, составить уравнения скалярного вида, спроецировав вектора на некую ось. 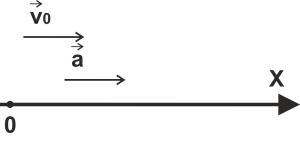 Рис. 1. Равноускоренное движение 1 Пример 1. Тело движется прямо с начальной скоростью  и ускоряется. По задаче выставляем вектора на ось OX (движение прямолинейное) (рис. 1). Сказано, что тело движется вдоль оси (вектор направлен по оси) и ускоряется (вектор также направлен вдоль оси). Осталось зафиксированные вектора спроецировать:Для уравнения (1):  Для уравнения (2):  В общем случае, мы не можем предугадать направления векторов  и , соответственно, мы не можем указать точный знак проекции этих векторов на выбранную ось. Но не заморачиваемся: в результате решения задачи мы получим одно и то же по модулю число, даже если ошибёмся. Т.е. выбираем направления как хотим, а потом анализируем ответ. Рис. 2. Равноускоренное движение-2 Пример 2. Тело движется в положительном направлении оси и затормаживает. По задаче тело движется вдоль оси (вектор направлен по оси), а торможение говорит о том, что вектор ускорения ( ) направлен против оси OX (рис. 2). Проецируем:Для уравнения (1):  Для уравнения (2): 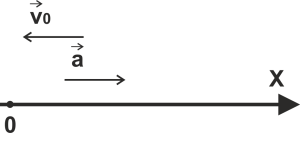  Рис. 3. Равноускоренное движение-3 Пример 3. Тело движется в отрицательном направлении оси и затормаживает. По задаче тело движется в обратную сторону оси OX (вектор направлен против оси), а торможение говорит о том, что вектор ускорения ( ) направлен против движения, а значит, по оси OX (рис. 3). Проецируем:Для уравнения (1):  Для уравнения (2):   Рис. 4. Равноускоренное движение-4 Пример 4. Тело движется в отрицательном направлении оси и ускоряется. По задаче тело движется в обратную сторону оси OX (вектор направлен против оси), а ускорение говорит о том, что вектор ускорения ( ) направлен в сторону движения, а значит, против оси OX (рис. 4). Проецируем:Для уравнения (1):  Для уравнения (2):  Вывод: только что мы получили восемь различных формул, применимых для решения задач. Очень не хотелось бы их помнить. К счастью, есть выход: запомнить и понять векторный вид этих уравнений (1) и (2), а далее, применительно к данной вам задаче, просто адаптировать их, используя проекции. Кроме формул (1) и (2), имеется ещё одна расчётная формула, которая чаще всего используется, когда в задаче на нужно найти время или его не дано. Воспользуемся уже имеющимися (1) и (2), считая движение тела равноускоренным. Выделим из (1) время:  (3)Подставим (3) в (2) при условии  := = =    (4)Таким образом, мы получили формулу, в которой нет параметра времени. 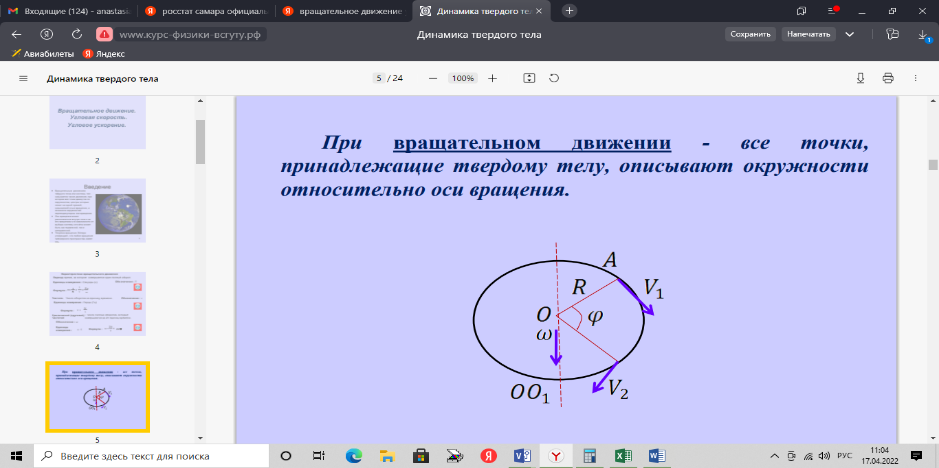 5. Вращательное движение характеризуется двумя величинами: • Линейная скорость V • Угловая скорость Угловой скоростью - называется отношение угла поворота радиуса R (угловой путь) к промежутку времени, за который этот поворот произошел.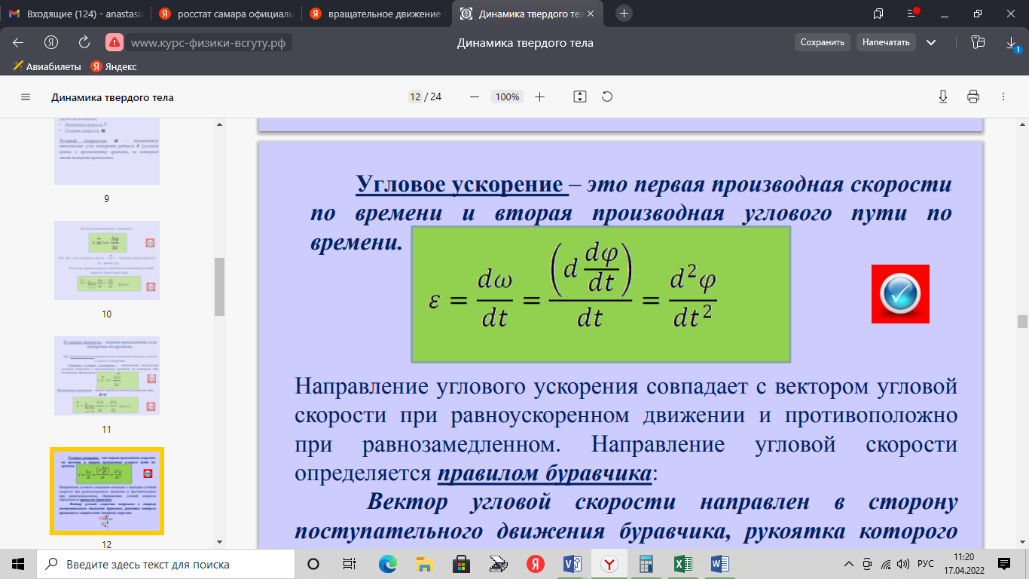 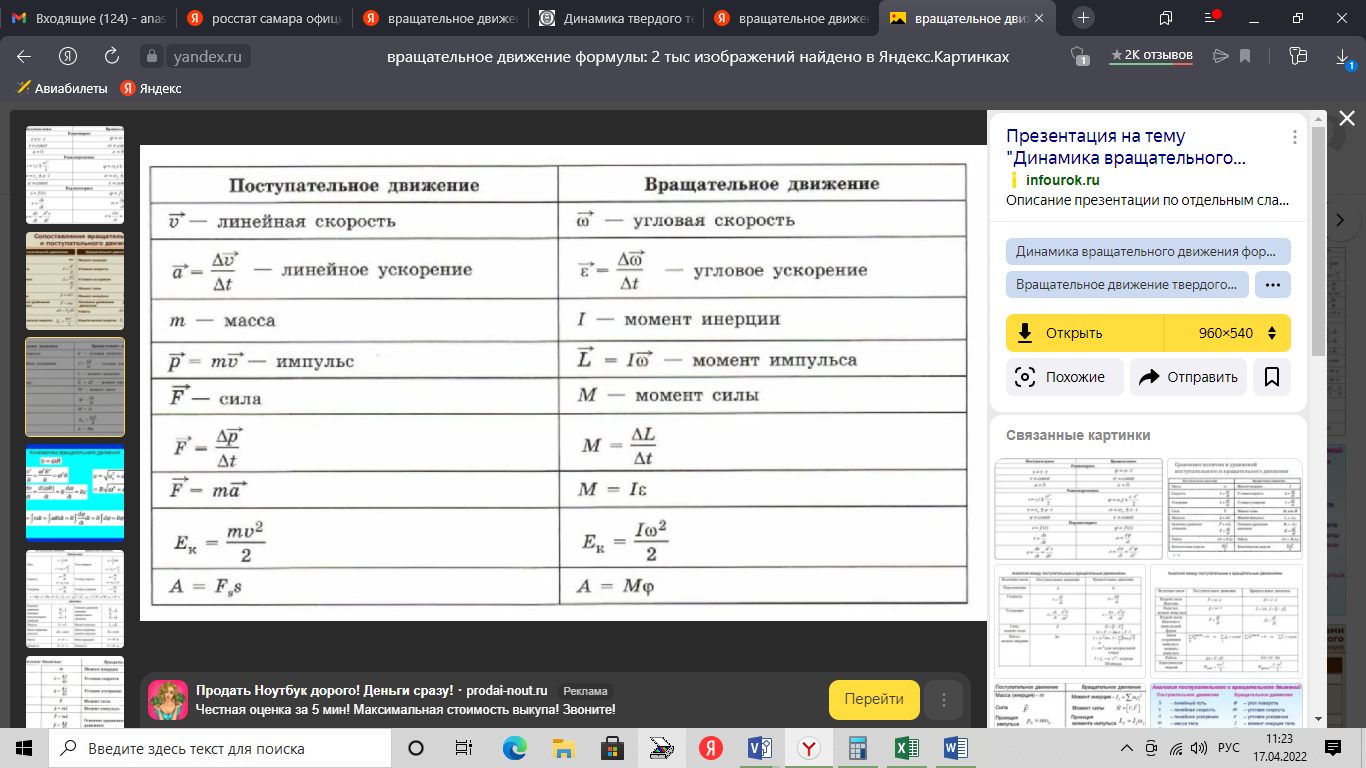  Угол поворота . В системе СИ измеряется в радианах = [1 рад] 2N Вопрос 6: Вопрос 7: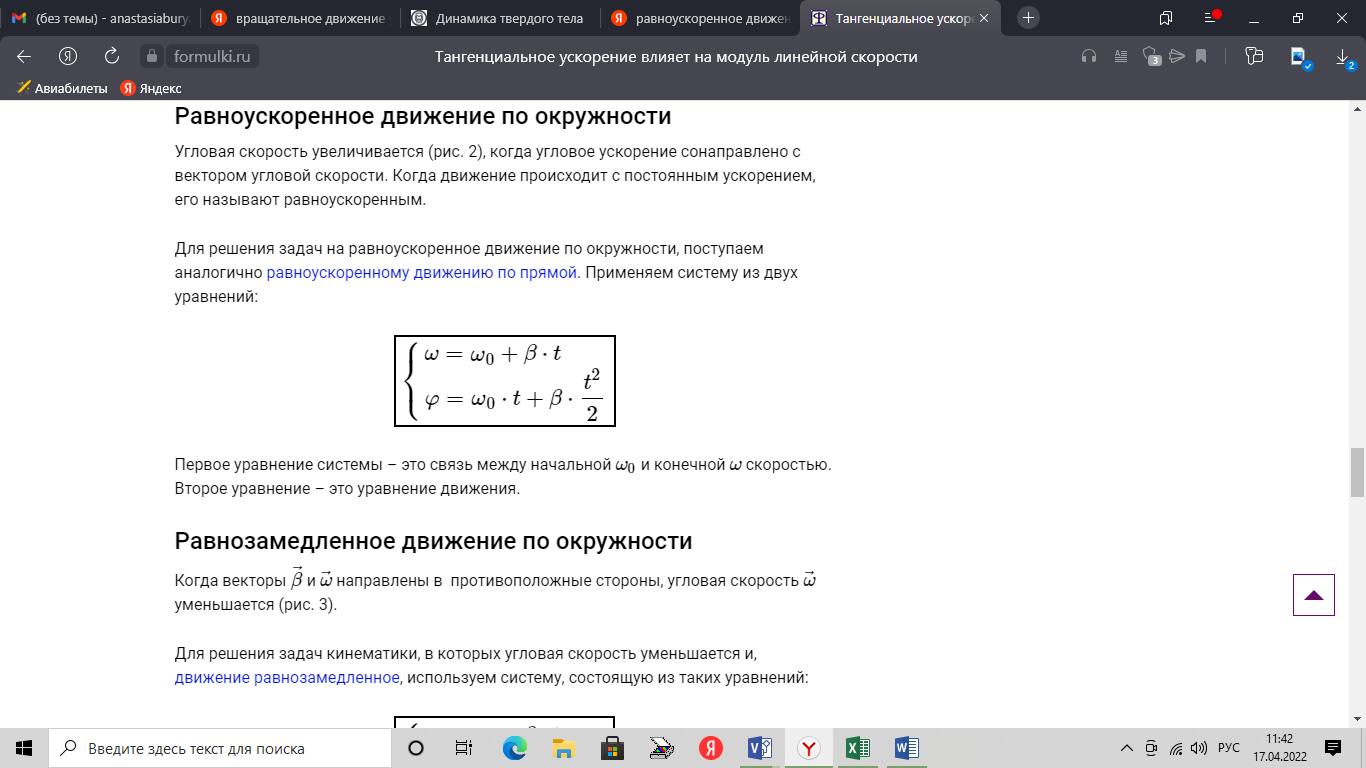 Вопрос 8:  9 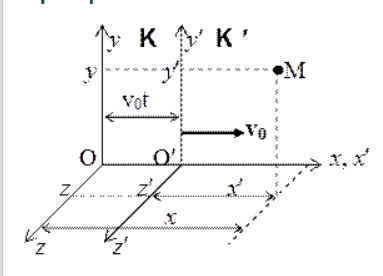 . Принцип Галилея. Никакими механическими опытами нельзя определить движется ИСО или покоится. Все ИСО равноправны. В неинерциальных системах отсчета (НИСО) тело может иметь ускорение без видимых на то причин, т.есть без взаимодействия. Инерция - это свойство тела сохранять состояние покоя или равномерного прямолинейного движения при отсутствии внешних воздействий или их взаимной компенсации.Инертность - это свойство тела изменять свою скорость при взаимодействии не мгновенно, а за конечный промежуток времени. Масса - это количественная мера инертности тела. Чем больше масса, тем медленнее тело изменяет свою скорость при взаимодействии. В системе СИ: m кг. 1  0. Второй закон Ньютона. 1. Произведение массы тела на вектор его ускорения равно векторной сумме сил, приложенных к телу (равнодействующей силе). Вектор ускорения тела прямо пропорционален вектору равнодействующей силы и обратно пропорционален массе тела. И   м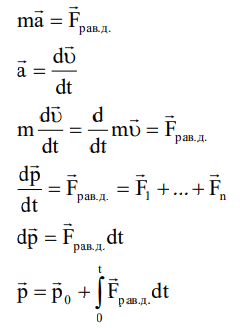пульс тела - это вектор, равный произведению массы тела на вектор его скорости. В системе СИ:  И  мпульс силы - это вектор, равный произведению вектора силы на время ее действия. В системе СИ:  3. Изменение импульса тела равно импульсу равнодействующей силы. Третья формулировка является наиболее общей формулировкой второго закона Ньютона и справедлива, даже если масса переменная. Т  ретий закон Ньютона.Силы, с которыми взаимодействуют два тела, равны по модулю и противоположны по направлению (сила действия равна по модулю и противоположна силе противодействия). Силы F12 и F21 приложены к разным телам. Складывать их нельзя. Можно складывать силы, приложенные к одному телу. 11. Импульсом тела называют векторную физическую величину, равную произведению массы тела на скорость его движения: p ⃗=mυ ⃗. Единицей импульса в СИ является килограмм на метр в секунду: 1 (кг·м)/с З  акон сохранения импульса: суммарный импульс тел, составляющих замкнутую систему, в результате взаимодействия тел системы не изменяется:Замкнутая система - это система, в которой внешние силы не действуют или сумма внешних сил равна нулю. 1 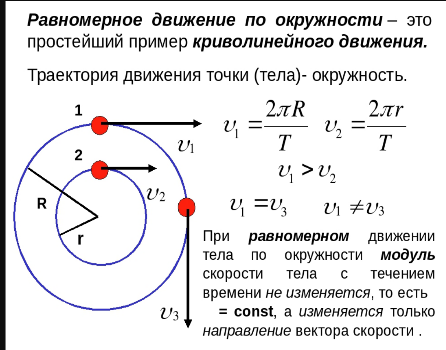 2.   13. Теорема Гюйгенса – Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс, и произведения массы тела на квадрат расстояния между осями. 1  4   15 16 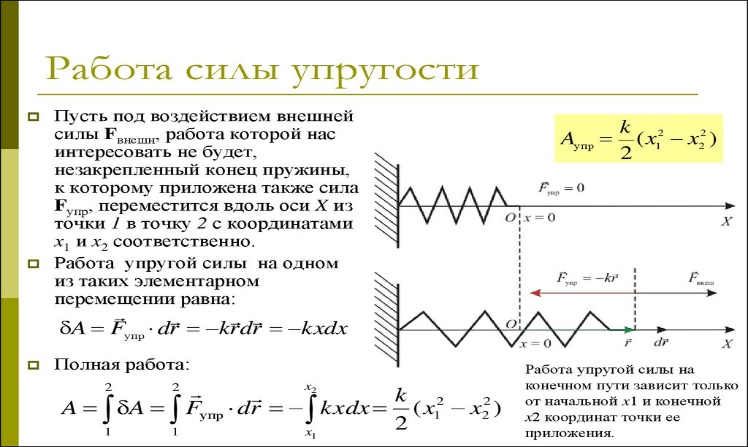   17.  |