яп зачет. Вопросы к япу 1 билет Понятие информации
 Скачать 0.51 Mb.
|
1 2 Классификация структур данныхПо сложности: простые интегрированные По способу представления: физическая логическая По наличию связей между элементами данных: несвязные связные По изменчивости: Статические полустатические динамические По характеру упорядоченности элементов в структуре: линейные нелинейные По виду памяти, используемой для сохранности данных: для оперативной для внешней памяти 18 билет Линейные структуры данных - это структуры данных, в которых переход от одного элемента данных к другому не зависит от каких-либо логических условий, т.е. в линейных структурах используются лишь безусловные связи элементов. АТД линейный список - базовая динамическая структура данных в информатике, состоящая из узлов, каждый из которых содержит как собственно данные, так и одну или две ссылки («связки») на следующий и/или предыдущий узел списка. Принципиальным преимуществом перед массивом является структурная гибкость: порядок элементов связного списка может не совпадать с порядком расположения элементов данных в памяти компьютера, а порядок обхода списка всегда явно задаётся его внутренними связями. Основные операции, представление и реализации Основные операции над линейным односвязным списком: перемещение по списку включение элемента в линейный односвязный список исключение элемента из линейного односвязного списка извлечение данных из любого элемента изменение данных любого элемента подсчет количества элементов списка Основные способы хранения линейных списков в памяти компьютера можно разделить на способы последовательного и связанного хранения. При последовательном хранении элементы списка располагаются в памяти в последовательных ячейках, при этом один элемент следует сразу же за другим. Связанное хранение представляет собой более гибкую схему, при которой каждый элемент списка содержит связь со следующим элементом, а их взаимное расположение в памяти может быть произвольным. Элементы такого списка линейно упорядочены. Кроме элементов в списке имеется навигатор, который может находиться в следующих позициях: в начале списка (то есть перед первым элементом списка); в конце списка (то есть за последним элементом списка); между элементами списка. Навигатор можно передвигать только от начала к концу списка на один элемент за раз. Кроме того, добавлять элементы списка можно только в позиции, на которую ссылается навигатор. А изменять/удалять/читать можно только элементы, которые находятся в позиции, предшествующей той, на которую ссылается навигатор, т.е. впереди по ходу его движения. АТД стек, очередь Стек — это набор данных, устроенный по принципу LIFO (Last In First Out) — последним пришел — первым вышел. Очередь (first-in, first-out - первым пришел, первым ушел, сокращенно FIFO) является еще одним фундаментальным АТД. Она похожа на стек магазинного типа, но с противоположным правилом удаления элемента: из очереди удаляется не последний вставленный элемент, а наоборот - элемент, который был вставлен в очередь раньше всех остальных. Основные операции, представление и реализации Над стеком реализованы следующие операции: инициализация стека init(s), где s — стек помещение элемента в стек push(s, i), где s — стек, i — помещаемый элемент удаление элемента из стека i=pop(s) получение верхнего элемента стека без его удаления i=stkTop(s), где s — стек получение количества элементов стека определение, пуст ли стек isempty(s) возвращает 1 если стек пустой и 0 в противном случае вывод элементов стека stkPrint(s), где s — стек Простейшие операции с очередью: init() инициализация очереди insert (q, x) — помещение элемента x в конец очереди q (q — указатель на очередь) x=remove (q) — удаление элемента x из очереди q isempty(q) — возвращает 1, если очередь пуста и 0 в противном случае print(q) – вывод элементов очереди q Существует несколько способов реализации стека: с помощью одномерного массива; с помощью связанного списка; с помощью класса объектно-ориентированного программирования. Существует несколько способов реализации очереди: с помощью одномерного массива; с помощью связанного списка; с помощью класса объектно-ориентированного программирования. Применение структур данных Структуры данных используются для хранения информации в упорядоченном виде. 19 билет Постановка задачи, основные определения Постановка задачи - это описание задачи по определенным правилам, которое дает исчерпывающее представление о ее сущности, логике преобразования информации для получения результата. Понятие внутренней и внешней сортировок, устойчивость сортировки, основные характеристики эффективности Внутренняя сортировка — разновидность алгоритмов сортировки или их реализаций, при которой объема оперативной памяти достаточно для помещения в неё сортируемого массива данных с произвольным доступом к любой ячейке и, собственно, для выполнения алгоритма. Внешняя сортировка — сортировка данных, расположенных на периферийных устройствах и не вмещающихся в оперативную память, то есть когда применить одну из внутренних сортировок невозможно. Стоит отметить, что внутренняя сортировка значительно эффективней внешней, так как на обращение к оперативной памяти затрачивается намного меньше времени, чем к магнитным дискам, лентам. Устойчивая сортировка — сортировка, которая не меняет относительный порядок сортируемых элементов, имеющих одинаковые ключи, по которым происходит сортировка. Устойчивость является очень важной характеристикой алгоритма сортировки, но тем не менее она практически всегда может быть достигнута путём удлинения исходных ключей за счёт дополнительной информации об их первоначальном порядке. Улучшенные алгоритмы внутренней сортировки Сортировка Шелла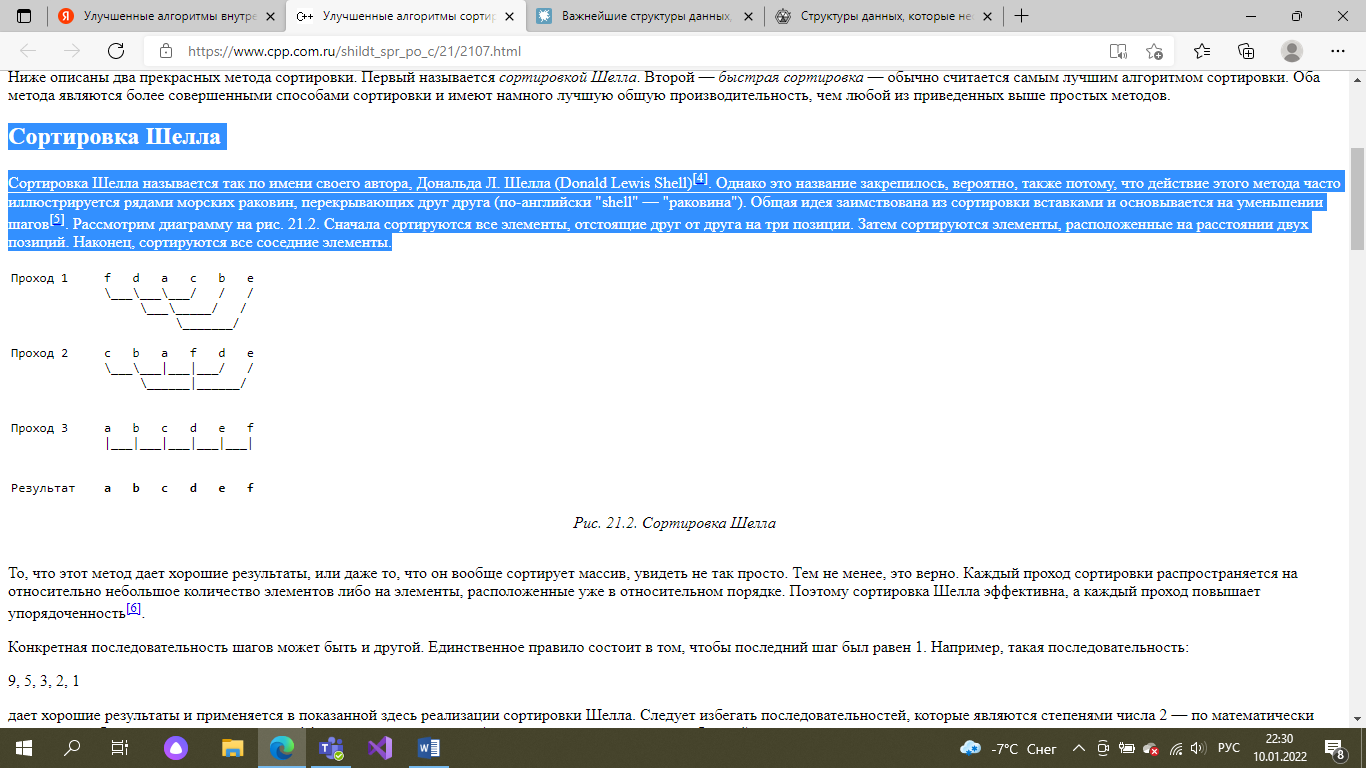 Общая идея заимствована из сортировки вставками и основывается на уменьшении шагов[5]. Рассмотрим диаграмму на рис. 21.2. Сначала сортируются все элементы, отстоящие друг от друга на три позиции. Затем сортируются элементы, расположенные на расстоянии двух позиций. Наконец, сортируются все соседние элементы.Быстрая сортировка В ее основе лежит сортировка обменами — удивительный факт, учитывая ужасную производительность пузырьковой сортировки! Быстрая сортировка построена на идее деления. Общая процедура заключается в том, чтобы выбрать некоторое значение, называемое компарандом (comparand)[10], а затем разбить массив на две части. Все элементы, большие или равные компаранду, перемещаются на одну сторону, а меньшие — на другую. Потом этот процесс повторяется для каждой части до тех пор, пока массив не будет отсортирован. Затем сортировка повторяется для обеих половин массива, то есть bса и def. Как вы видите, этот процесс по своей сути рекурсивный, и, действительно, в чистом виде быстрая сортировка реализуется как рекурсивная функция[11]. Значение компаранда можно выбирать двумя способами — случайным образом либо усреднив небольшое количество значений из массива. Для оптимальной сортировки необходимо выбирать значение, которое расположено точно в середине диапазона всех значений. Однако для большинства наборов данных это сделать непросто. В худшем случае выбранное значение оказывается одним из крайних. Тем не менее, даже в этом случае быстрая сортировка работает правильно. В приведенной ниже версии быстрой сортировки в качестве компаранда выбирается средний элемент массива. Модификации быстрой сортировки Вычисление порядковых статистик Описание алгоритмаБудем использовать процедуру рассечения массива элементов из алгоритма сортировки QuickSort. Пусть нам надо найти k-ую порядковую статистику, а после рассечения опорный элемент встал на позицию m. Возможно три случая: k = m. Порядковая статистика найдена. k < m. Рекурсивно ищем k-ую статистику в первой части массива. k > m. Рекурсивно ищем (k−m−1)-ую статистику во второй части массива. Сортировка слиянием Сортировки слиянием работают по такому принципу: Ищутся (как вариант — формируются) упорядоченные подмассивы. Упорядоченные подмассивы соединяются в общий упорядоченный подмассив. Сам по себе какой-нибудь упорядоченный подмассив внутри массива не имеет особой ценности. Но если в массиве мы найдём два упорядоченных подмассива, то это совершенно другое дело. Дело в том, что очень быстро и с минимальными затратами можно произвести над ними слияние — сформировать из пары упорядоченных подмассивов общий упорядоченный подмассив. Шейкерная сортировка (также известна как сортировка перемешиванием и коктейльная сортировка). Заметим, что сортировка пузырьком работает медленно на тестах, в которых маленькие элементы стоят в конце (их еще называют «черепахами»). Такой элемент на каждом шаге алгоритма будет сдвигаться всего на одну позицию влево. Поэтому будем идти не только слева направо, но и справа налево. Будем поддерживать два указателя begin и end, обозначающих, какой отрезок массива еще не отсортирован. На очередной итерации при достижении end вычитаем из него единицу и движемся справа налево, аналогично, при достижении begin прибавляем единицу и двигаемся слева направо. Асимптотика у алгоритма такая же, как и у сортировки пузырьком, однако реальное время работы лучше. 1 2 |