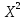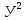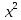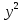ПЗ ЭКОНОМЕТРИКА. ЭКОНОМЕТРИКА. Вопросы Укажите основные этапы эконометрического исследования
 Скачать 25.36 Kb. Скачать 25.36 Kb.
|
|
Вопросы: 1. Укажите основные этапы эконометрического исследования. Определение цели исследования. Построение системы показателей и логический отбор факторов, которые в наибольшей степени влияют на каждый показатель. Выбор формы связи изучаемых показателей между собой и отобранными факторами. Сбор исходных данных, их преобразование и анализ. Построение эконометрической модели и определение ее параметров. Проверка качества построенной модели, в первую очередь, ее адекватности изучаемому экономическому процессу. Использование модели для экономического анализа и прогнозирования. 2. Назовите виды аналитических зависимостей, наиболее часто используются при построении моделей Линейная Степенная Полулогарифмическая Гиперболическая Экспоненциальная 3. Охарактеризуйте функции, которые чаще всего используются для построения уравнения парной регрессии Линейная регрессия Регрессии, нелинейные по объясняющим переменным: а) Полиномы разных степеней б) Равносторонняя гипербола Регрессии, нелинейные по оцениваемым параметрам а) Степенная б) Показательная в) Экспоненциальная 4. Укажите, по какой формуле вычисляется выборочный коэффициент парной корреляции rxy 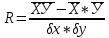 5. Объясните сущность метода анализа динамического ряда Комплексный анализ динамических рядов, как правило, включает не только расчет характеристик интенсивности изменения уровней ряда при переходе от одного момента или промежутка времени к другому (абсолютных приростов, коэффициентов и темпов роста и прироста), а также нахождение обобщенных средних характеристик (среднего уровня ряда, средних темпов роста и прироста), но и выявление основных закономерностей в развитии динамического ряда. ЗАДАНИЕ: Рассчитать коэффициенты для различных видов зависимостей. Исходные данные в табл.3 Таблица 3. Регрессионный анализ.
На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер. Линейное уравнение регрессии имеет вид y = bx + a Оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где ei – наблюдаемые значения (оценки) ошибок εi, a и b соответственно оценки параметров α и β регрессионной модели, которые следует найти. Для оценки параметров α и β - используют МНК (метод наименьших квадратов). Система нормальных уравнений. a·n + b·∑x = ∑y a·∑x + b·∑x2 = ∑y·x Для расчета параметров регрессии построим расчетную таблицу (табл. 1)
Для наших данных система уравнений имеет вид 5a + 150·b = 350 150·a + 5500·b = 12500 Получаем эмпирические коэффициенты регрессии: b = 2, a = 10 Уравнение регрессии (эмпирическое уравнение регрессии): y = 2 x + 10 Ковариация. cov xy = 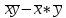 = 2500 – 30 * 70 = 400 = 2500 – 30 * 70 = 400Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции. r xy = 2500 – 30*70 / 14.142*28.284 = 1 Линейный коэффициент корреляции принимает значения от –1 до +1. Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока: 0.1 < rxy < 0.3: слабая; 0.3 < rxy < 0.5: умеренная; 0.5 < rxy < 0.7: заметная; 0.7 < rxy < 0.9: высокая; 0.9 < rxy < 1: весьма высокая; В нашем примере связь между признаком Y и фактором X весьма высокая и прямая. Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии b: r x,y = b * S(x) / S(y) = 2* 14.142/28.284 = 1 Вывод: Изучена зависимость Y от X. На этапе спецификации была выбрана парная линейная регрессия. Оценены её параметры методом наименьших квадратов. Возможна экономическая интерпретация параметров модели - увеличение X на 1 ед.изм. приводит к увеличению Y в среднем на 2 ед.изм. 2. Вычислить коэффициент корреляции для линейной зависимости. Исходные данные в таблице 4. Таблица 4. Корреляционный анализ.
Для этого построим вспомогательную таблицу:
r = (19610 – 150*(448/5)) / ( 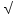 ((5500-150*150/5) * (87090-448*448/5))) = 0.9005 ((5500-150*150/5) * (87090-448*448/5))) = 0.9005Вывод: Полученное значение коэффициента корреляции говорит о наличии прямой связи между Х и У. Величина коэффициента корреляции показывает, что связь между Х и У сильная (очень тесная). |