Лабораторная работа 1 Построение уравнения парной регрессии по эмпирическим данным Цель и задачи выполнения лабораторной работы

• Название: Лабораторная работа 1 Построение уравнения парной регрессии по эмпирическим данным Цель и задачи выполнения лабораторной работы
• Дата: 25.05.2022
• Размер: 168.16 Kb.
• Имя файла: Laboratornaya (1).docx
• Тип: Лабораторная работа; #548231
• страница: 1 из 9

ВЫПОЛНИТЬ ОТЧЕТ ПО ЛАБОРАТОРНОЙ №1

Лабораторная работа № 1

Построение уравнения парной регрессии по эмпирическим данным

1. 
   Цель и задачи выполнения лабораторной работы
   

Лабораторная работа по дисциплине «Эконометрика» предусмотрена учебным планом специальности 080105 «Финансы и кредит» для очной формы обучения.

Целью работы является приобретение практических навыков построения эконометрических моделей парной регрессии с использованием наиболее доступного табличного процессора Microsoft Excel.

Основными задачами является: построения моделей парной регрессии, с использованием программного продукта Microsoft Excel и оценка адекватности модели.

2. 
   Теоретические основы метода построения эконометрических моделей парной регрессии
   

Парная регрессия - уравнение связи двух переменных у и х:
у = а + b ·x + u (1)
где у — зависимая переменная (результативный признак);

х - независимая, объясняющая переменная (признак-фактор);

u –случайная компонента.

Построение уравнения регрессии сводится к оценке ее парамет­ров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических ŷ_хминимальна, т.е.
∑ ( у- ŷ_i )² → min.
Для линейных и нелинейных уравнений, приводимых к линей­ным, решается следующая система относительно а и Ь:
n · a + b ·∑x = ∑y,

a ·∑x + b ·∑x² = ∑x ·y.
Можно воспользоваться готовыми формулами, которые вытека­ют из этой системы:

a = yср – b ·xср,

b = cov ( x, y ) / σ² (x)
Расчетные соотношения имеют вид:

a = yср – b ·xср,

b = ( ∑ x_i· y_i – n ·xср ·y_ср) / (∑ x_i²- n (·x_ср)² ) (2)


Оценку качества построенной модели даст коэффициент (ин­декс) детерминации ( R² )

_ _
R² = ( ∑ ( ŷ_i - yср)² ) / ( ∑ ( y_i - yср)² ) (3)
где yср – среднее значение y;

xср – среднее значение x;

ŷ_i – вычисленные по уравнению регрессии значения;

y_i – эмпирические значения зависимой переменной.

При этом выполняется соотношение:

∑ ( y_i – yср )² = ∑ ( ŷ_i - yср)² + ∑ (y_i – ŷ_i)² (4)

где ∑ ( y_i – yср )² - общая сумма квадратов отклонений;

∑ ( ŷ_i–yср)² - сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);

∑ (y_i– ŷ_х)² - остаточная сумма квадратов отклонений.

Коэффициент детерминации может быть преобразован с учетом (4)

R² =1– ( ∑ ( ŷ_i – y_i)² ) / ( ∑ (y_i – yср)² ) (5)
Вычисление по приведенным выше зависимостям (1-5) удобно производить воспользовавшись расчетной таблицей № 1.

Таблица 1.

№ наблюдения	xi	yi	xi· yi	ŷi = a+b·xi	( yi - ŷi)²	( yi – yср )²	xi²	( xi – xср )²
1
2
...
n
Сумма	∑ xi	∑ yi	∑ xi· yi	∑ ŷi	∑(yi- ŷi)²	∑( yi – yср )²	∑ xi²	∑( xi– xср )²
Сумма/n	_ x	_ y	-	-	-	-	-	σ² (x)

3. 
   Оценка адекватности уравнения регрессии и значимости параметров уравнения
   

Для оценки адекватности модели в целом используется F – критерий Фишера. По этому критерию проверяется нулевая гипотеза о статистической не значимости уравнения регрессии. Согласно общей методике проверки статистических гипотез сперва необходимо назначить уровень значимости – вероятность ошибочного решения принятия нулевой гипотезы. Эту величину назначают исходя из последствий ошибочного решения обычно в интервале (1 – 10)%. Затем вычисляют фактическое значение F – критерия (Fф).

Fф = (( ∑ (ŷ_i – yср)²/m)/(( ∑ ( ŷ_i – y_i)² ) /(n-m-1))

где n - объем выборки;

m – число объясняющих переменных.

Критическое значение F – критерия (Fкр) можно определить пользуясь соответствующими таблицами или встроенными стандартными статистическими функциями при числе степеней свободы числителя к1= m и числе степеней свободы знаменателя к2= n-m-1. Если Fф > Fкр, то нулевая гипотеза отвергается – модель адекватна; если Fф < Fкр, то нулевая гипотеза принимается и модель может быть отвергнута. Проверка значимости коэффициентов уравнения регрессии производится по t – критерию Стьюдента. Проверка осуществляется для каждого коэффициента при ранее принятом уровне значимости в следующей последовательности. Определяют фактическое значение t – критерия (t_ф).

t _ф(b) = (b-0)/σ(b), при b>0 и t _ф(b) = (0-b)/σ(b), при b< 0,

где σ(b) – стандартная ошибка коэффициента b.

σ(b) = 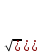((∑ ( y_i - ŷ_i) ²)/(n-2))/ ∑( x_i– xср )²)

Содержание нулевой гипотезы: коэффициент b =0.

Если tкр > tф, то принимается нулевая гипотеза и значение коэффициента следует принять равным 0. Если tкр < tф, то нулевая гипотеза отвергается и значение коэффициента принимается равным ранее вычисленному по формулам (2).

Аналогично будет производится проверка для коэффициента a уравнения. Значение стандартной ошибки определяем по формуле

σ(a) = 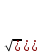((∑ ( y_i - ŷ_i )² ∑x_i²) /(n-2)/ n/∑( x_i– xср )²).

4. 
   Содержание задания
   

Построить уравнение регрессии, вычислить коэффициент детерминации, воспользовавшись табличным процессором Excel в режиме непосредственных вычислений, используя форму расчетной таблицы №1 и соотношения (1-5); вычислить коэффициенты уравнения регрессии осуществить проверку адекватности модели и значимость коэффициентов уравнения регрессии для примера согласно табл.2 и индивидуального задания, содержащегося в приложении (табл.1).

В отчете по лабораторной работе должны содержаться основные расчетные соотношения, результаты вычислений по индивидуальному заданию, результаты прогноза по модели для значения объясняющей переменной (x=26), а также выводы по работе.

5. 
   Пример расчетов в табличной форме
   

Имеются эмпирические данные зависимости прибыли (y) от стоимости основных фондов (x).