Лабораторная работа 1 Построение уравнения парной регрессии по эмпирическим данным Цель и задачи выполнения лабораторной работы
 Скачать 168.16 Kb. Скачать 168.16 Kb.
|
|
Отчет должен содержать: цель работы, исходные данные, результаты расчетов, выводы по работе. Лабораторная работа № 3 Построение нелинейных регрессионных моделей Цель работы: изучение методов построения моделей нелинейных процессов. Одним из недостатков линейного регрессионного анализа является то, что он может быть использован для описания результативного признака только приближенного линейно зависящего от независимых переменных. Это, безусловно, не удовлетворяет ученых и практиков, работающих в области финансов. Некоторые функции достаточно просто могут быть прообразованы к линейному виду, например: y1=b0+b1/x; (1) y2= b0+b1  +b2·x22; (2) +b2·x22; (2)y3=b0·xb1. (3) Уравнения (1) и (2) легко могут быть приведены к линейным путем простой замены переменных. Для (1) заменой может служить z=1/x, а для (2) z1=  ; z2=x22. В этом случае уравнения (1) и (2) примут вид линейных: ; z2=x22. В этом случае уравнения (1) и (2) примут вид линейных:y1=b0+b1·z; y2=b0+b1·z1+b1·z2. Такие уравнения принято считать внутренне линейными и для использования алгоритма линейной регрессии достаточно преобразовать массивы независимых переменных согласно известной функциональной зависимости. Уравнение (3) описывает степенную зависимость результативного показателя (y) от переменной (х). Замена z= xb1 не позволит решить проблему, т. к. показатель степени b1 не известен. Такое уравнение будет нелинейным по параметрам, которые и необходимо определить. Уравнения вида (3) могут быть легко приведены к линейному виду путем логарифмирования обеих его частей по любому основанию. y= b0·xb1; ln y=ln b0+b1·ln x. (4) Обозначим: ln y=Y; ln b0=B0; ln x=X; тогда (4) примет вид: Y=B0+b1X. Значения B0, b1 находим пользуясь обычной методикой для линейных зависимостей. Значение b0 найдем потенцируя B0: b0=exp (B0). Аналогично может быть преобразована к линейному виду и показательная функция. y=b0·b1x. ln y=ln b0+x·ln b1. (5) Обозначим: ln b0=B0; ln b1=B1; ln y=Y; тогда (5) примет вид: Y=B0+B1·x. Значения неизвестных параметров найдем: b0=exp (B0); b1=exp (B1). Пример: Производственная функция. Эта функция показывает зависимость показателей реального объема выпуска (Y) от капитальных затрат (К) и затрат труда (L). В практике исследований используется несколько функциональных зависимостей: Линейная y= b0+b1·K+b2·L; Кобба-Дугласа y=A·Kα·Lβ; С постоянной эластичностью замещения и т. д. Имеются значения индексов реального объекта производства, капитальных затрат и затрат труда в промышленности США за 1899-1922 гг. (1899 г. взят за 100%) [7]. Таблица 1. Производственная функция.
Построить уравнения линейной регрессии с использованием логарифмического преобразования. Сравнить результаты на основе R2, сделать выводы. Прежде чем использовать методику построения уравнения регрессии, необходимо выявить тип закономерности, лежащей в основе изучаемого явления. Часто общий вид закономерности можно получить по литературным источникам, относящимся к изучаемому явлению. Однако не учет влияния каких-то важных факторов может существенно исказить проявление изучаемого процесса. Поэтому предварительно необходимо ответить на следующие вопросы: Насколько однородными являются выборочные данные? Каков количественный характер действия факторов на результативный показатель? Происходили ли какое-либо качественные изменения объекта в изучаемый период времени? Начинать исследование целесообразно (за исключением тех случаев, когда точно известна функциональная зависимость) с линейной функции: y=b0+b1·x1+b2·x2+..., являющийся частным случаем полиномиальной зависимости порядка более 1. Далее можно использовать следующие функции: гиперболическая зависимость: y=1/( b0+b1·x1+b2·x2+... ) k; показательная зависимость: y=b0·b1x1·b2x2... (bi>0); логарифмическая зависимость: y=b0+b1·ln x1+... ; степенная зависимость: y=b0·x1b1·x2b2..., bi могут принимать положительные и отрицательные значения; логистическая зависимость: y= 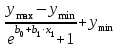 . .При наличии периодичностей могут использоваться функции y=А·sin x или y=B·cos x. Однако определение параметров уравнения в последних двух случаях возможно с использованием специальных процедур, базирующихся на приближенных методах. Пример: (К. Доугерти. Введение в эконометрику): Функция спроса на продукты питания (определяется естественными потребностями) в зависимости от дохода характеризуется насыщением. Имеются данные по потреблению продукта питания (у) в зависимости от дохода (х) [7]. Таблица 2. Потребление продукта в зависимости от дохода.
Построить уравнения, используя: линейную функцию y=b0+b1·x; степенную функцию y=b0+b1·xα, при этом подобрать наилучшую функциональную зависимость, используя прием замены переменной, изменяя показатель степени исходя из критерия max R2 ( -1≤α≤1). степенную функцию вида: y=b0·x1b1 показательную функцию: y=b0·b1·exp(x). Варианты 3) и 4) реализовать, используя логарифмическое преобразование. Задание: В соответствии с вариантом индивидуального задания построить уравнение линейной регрессии, подобрать функциональную зависимость и ее параметры наилучшим образом (по R2) описывающие эмпирические данные. Оценить точность описания моделью эмпирических данных, оценить значимость уравнения и значимость параметров уравнения регрессии. Сделать выводы. Отчет должен содержать: Результаты моделирования производственный функции; Результаты моделирования функций спроса; Результаты моделирования по варианту выбранного задания. Варианты индивидуального задания
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
