Лабораторная работа 1 Построение уравнения парной регрессии по эмпирическим данным Цель и задачи выполнения лабораторной работы
 Скачать 168.16 Kb. Скачать 168.16 Kb.
|
Таблица 2.млн. руб.
Воспользовавшись таблицей 1 и расчетными соотношениями (1-4), получим таблицу 3. Таблица 3.
R² = 0,944718 σ(b) = 0,035; t ф(b)=8,268; σ(а) = 12,797; t ф(a)=1,934; Fф =68,35; Fкр = 7,71 при уровне значимости 5% и Fкр =3,16 при уровне значимости 15%. Условие Fф > Fкр выполняется, уравнение адекватно. Значения tкр=2,777 при уровне значимости 5% В этом случае (tф(b)=8,268) > (tкр=2,777), а (tф(a)=1,934) < (tкр=2,777).Коэффициент a следует принять равным нулю, а коэффициент b =0,291. При принятии уровня значимости равным 15% tкр=1,778. В этом случае оба коэффициента значимо отличаются от нуля; a=24,752; b=0,291. Окончательно уравнение регрессии будет иметь вид: Y=24.752 +0.291*X. Лабораторная работа № 2 Построение эконометрических моделей множественной регрессии Цель работы: Ознакомление с ППП «Пакет анализа», «Регрессия»; построение моделей множественной регрессии. Общие сведения о надстройке «Пакет анализа» MS Excel Модель парной регрессии может иметь высокий уровень прогностических возможностей, если влиянием других факторов можно пренебречь. Как правило это справедливо при незначительном интервале изменения объясняющей переменной. Однако следует считать, что в большинстве случаев использование уравнения парной регрессии не обеспечивает требуемой точности. В уравнении множественной регрессии присутствует несколько объясняющих переменных, что позволяет учесть влияние требуемого количества факторов. у = а +∑(bi ·xi ) + u В настоящее время для получения множественной модели может быть использовано множество пакетов прикладных программ. Наибольшее распространение в деловой сфере получил табличный процессор Microsoft Excel, который, по данным еженедельника ComputerWeek, еще в конце 1995 г. использовали в своей деятельности более 60 % московских организаций, в том числе и для статистического анализа информации. В последние годы популярность Excel еще более возросла, что объясняется его органичной интеграцией в пакет Microsoft Office (начиная с Microsoft Excel 7.0 for Windows 95). Для проведения статистической обработки информации табличный процессор Microsoft Excel включает в себя программную надстройку «Пакет анализа» и библиотеку из 78 статистических функций. В повседневной деятельности такого набора инструментов бывает, как правило, вполне достаточно для проведения довольно полного и качественного статистического анализа информации. Технология работы с «Пакетом анализа» в режиме «Анализ данных» Выберем в меню Сервис пункт Анализ данных..., появится окно с одноименным названием (рис. 1). Это окно - по существу «центр управления» надстройки Пакет анализа, главным элементом которого является область Инструменты анализа. В данной области представлен список реализованных в Microsoft Excel методов статистической обработки данных: • «Гистограмма»; • «Выборка»; • «Описательная статистика»; • «Ранг и персентиль»; • «Генерация случайных чисел»; • «Двухвыборочный z-тест для средних»; • «Двухвыборочный t-тест с одинаковыми дисперсиями»; • «Двухвыборочный t-тест с различными дисперсиями»; • «Двухвыборочный F-тест для дисперсий»; • «Парный Двухвыборочный t-тест для средних»; • «Однофакторный дисперсионный анализ»; • «Двухфакторный дисперсионный анализ без повторений»; • «Двухфакторный дисперсионный анализ с повторениями»; • «Ковариация»; • «Корреляция»; • «Регрессия»; • «Скользящее среднее»; • «Экспоненциальное сглаживание»; • «Анализ Фурье». 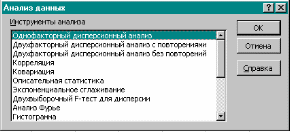 Рис. 1 Каждый из перечисленных методов реализован в виде отдельного режима работы, для активизации которого необходимо выделить соответствующий метод указателем мыши и щелкнуть по кнопке ОК. После появления диалогового окна вызванного режима можно приступать к работе. Диалоговое окно каждого режима включает в себя элементы управления (поля ввода, раскрывающиеся списки, флажки, переключатели и т. п.), которые задают определенные параметры выполнения режима (в качестве примера на рис. 2 изображено диалоговое окно режима «Регрессия»). Одна часть параметров является специфической и присуща только одному (или малой группе) режиму работы. Назначение таких параметров будет рассмотрено при изучении технологий работы с соответствующими режимами. Другая часть параметров универсальна и присуща всем (или подавляющему большинству) режимам работы. Элементами управления, задающими такие параметры, являются: 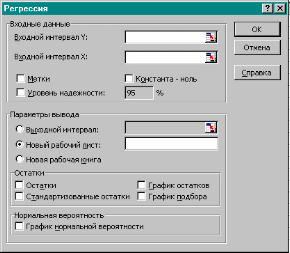 Рис. 2. 1. Поле Входной интервал - вводится ссылка на ячейки, содержащие анализируемые данные. 2. Переключатель Группирование - устанавливается в положение По столбцам или По строкам в зависимости от расположения данных во входном диапазоне. 3. Флажок Метки - устанавливается в активное состояние, если первая строка (столбец) во входном диапазоне содержит заголовки. Если заголовки отсутствуют, флажок следует дезактивировать. В этом случае будут автоматически созданы стандартные названия для данных выходного диапазона. 4. Переключатель Выходной интервал/Новый рабочий лист/Новая рабочая книга. В положении Выходной интервал активизируется поле, в которое необходимо ввести ссылку на левую верхнюю ячейку выходного диапазона. Размер выходного диапазона будет определен автоматически, и на экране появится сообщение в случае возможного наложения выходного диапазона на исходные данные. В положении Новый рабочий лист открывается новый лист, в который начиная с ячейки А1 вставляются результаты анализа. Если необходимо задать имя открываемого нового рабочего листа, введите его имя в поле, расположенное напротив соответствующего положения переключателя. В положении Новая рабочая книга открывается новая книга, на первом листе которой начиная с ячейки А1 вставляются результаты анализа. Содержание задания Задание 1. По данным табл.2 из лабораторной работы №1 построить уравнение парной регрессии. Задание 2. По индивидуальному заданию (приложение (табл.1)) построить уравнение множественной регрессии. Оба задания предполагают проведение следующих работ: используя табличный процессор Excel, надстройку «Пакет анализа», «Регрессия» оценить точность модели по коэффициенту детерминации; провести проверку адекватности модели и значимости ее коэффициентов, записать доверительные интервалы для коэффициентов. Обратимся к меню «Пакет анализа», «Регрессия» и введем исходные данные в диалоговом окне согласно рис. 3. С порядком ввода исходной информации, а также представлением результатов расчета можно ознакомиться, активизировав кнопку «справка» (рис.3). 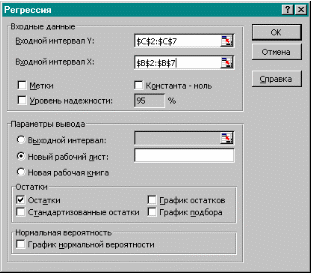 Рис. 3. Результаты вычислений приведены в таблицах 4, 5, 6, и 7. Таблица 4.
Таблица 5.
Таблица 6.
Таблица 7.
Результаты расчетов, приведенных в табл.4-7 позволяют получить значения параметров модели, все необходимые выводы относительно адекватности полученной модели, значимости ее параметров, точности описания моделью фактических данных. Из табл. 4 – 7 следует, что получено уравнение регрессии Y = 24.75+0.29·X. Полученная модель адекватна с вероятностью ошибки не более р=0,0011;коэффициенты модели значимо отличаются от 0 с вероятностями ошибки р(а) < 0,125 для коэффициента а=24,75 и р(b) < 0,0011 для коэффициента b = 0,29. Этот пакет прикладных программ позволяет получить множественную регрессионную модель с числом объясняющих переменных до 16. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

