Навигация по странице:Ответ
|
Возобновляемые и ресурсосберегающие источники энергии (1). Возобновляемые и ресурсосберегающие источники энергии
Задача 1. Ширина запрещенной зоны для Gа1-х AlxAs при х = 0,6 равна 1,8 эВ, Вычислить оптимальную длину волны излучения для фотоэлектрической генерации в солнечном элементе, изготовленном из этого материала.
Решение.
Оптимальная длина волны определяется соотношением
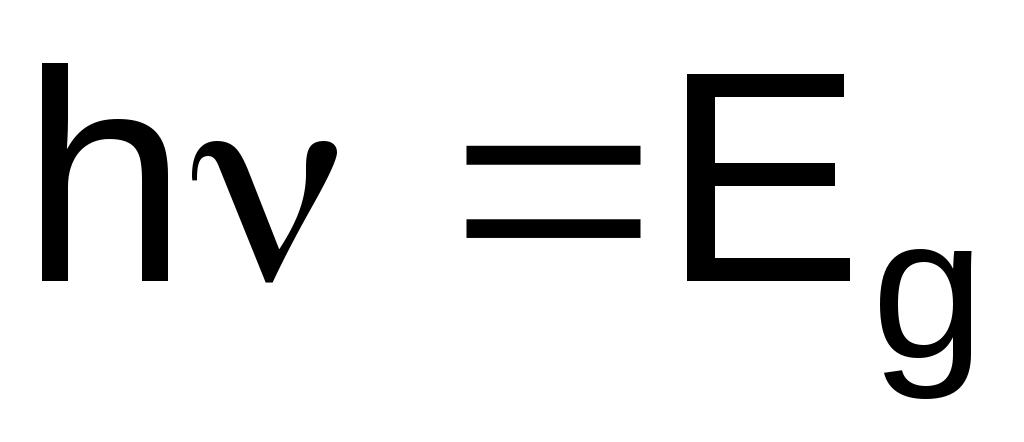 , (1) , (1)
где ν – оптимальная частота излучения; h – постоянная Планка;
Eg – ширина запрещенной зоны.
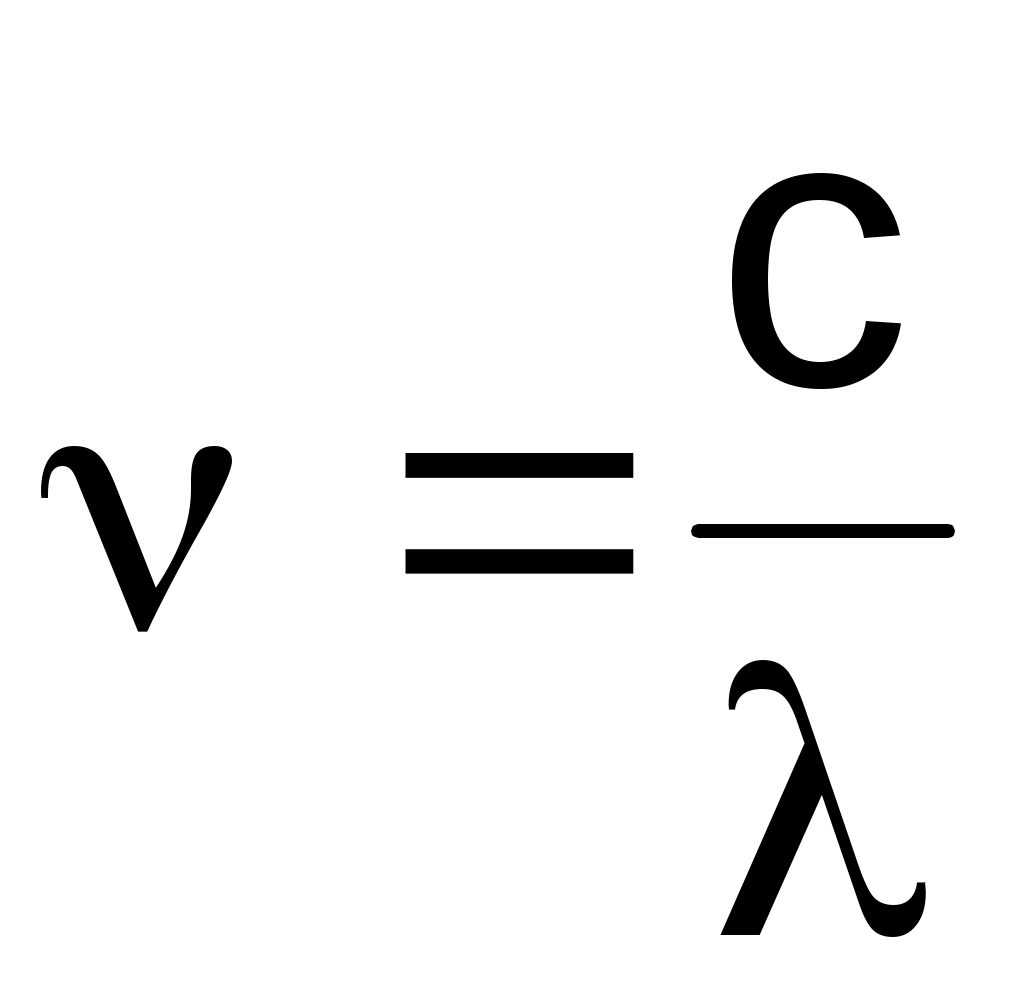 , (2) , (2)
где – длина волны падающего излучения.
Подставив (2) в (1), получим
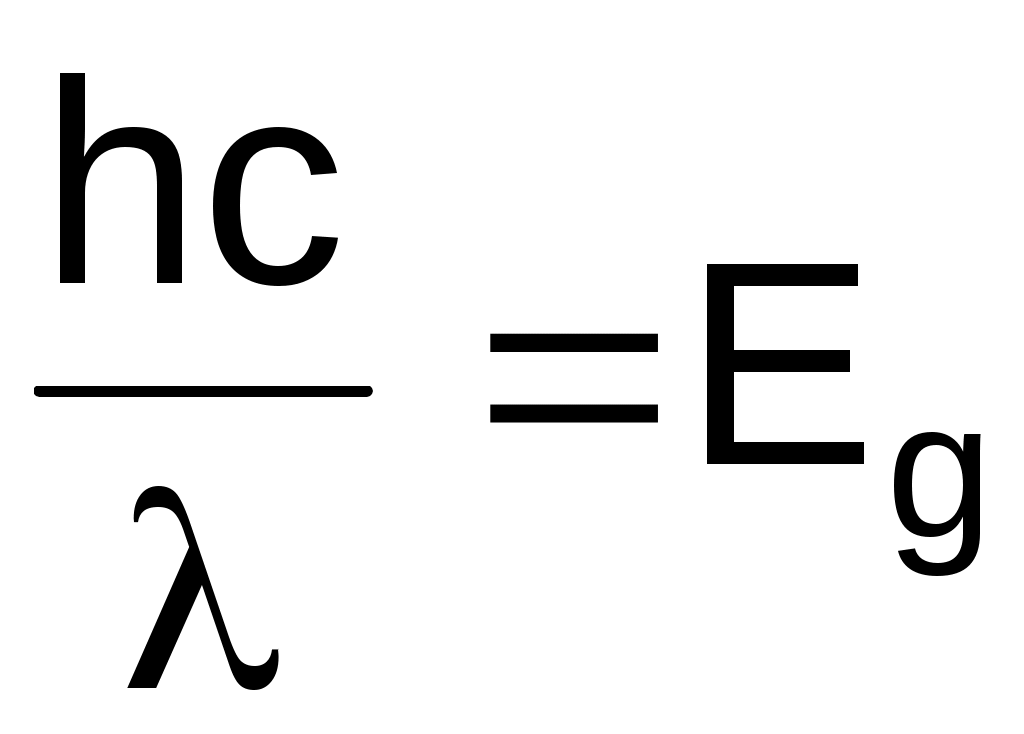 . (3) . (3)
Из (3) имеем
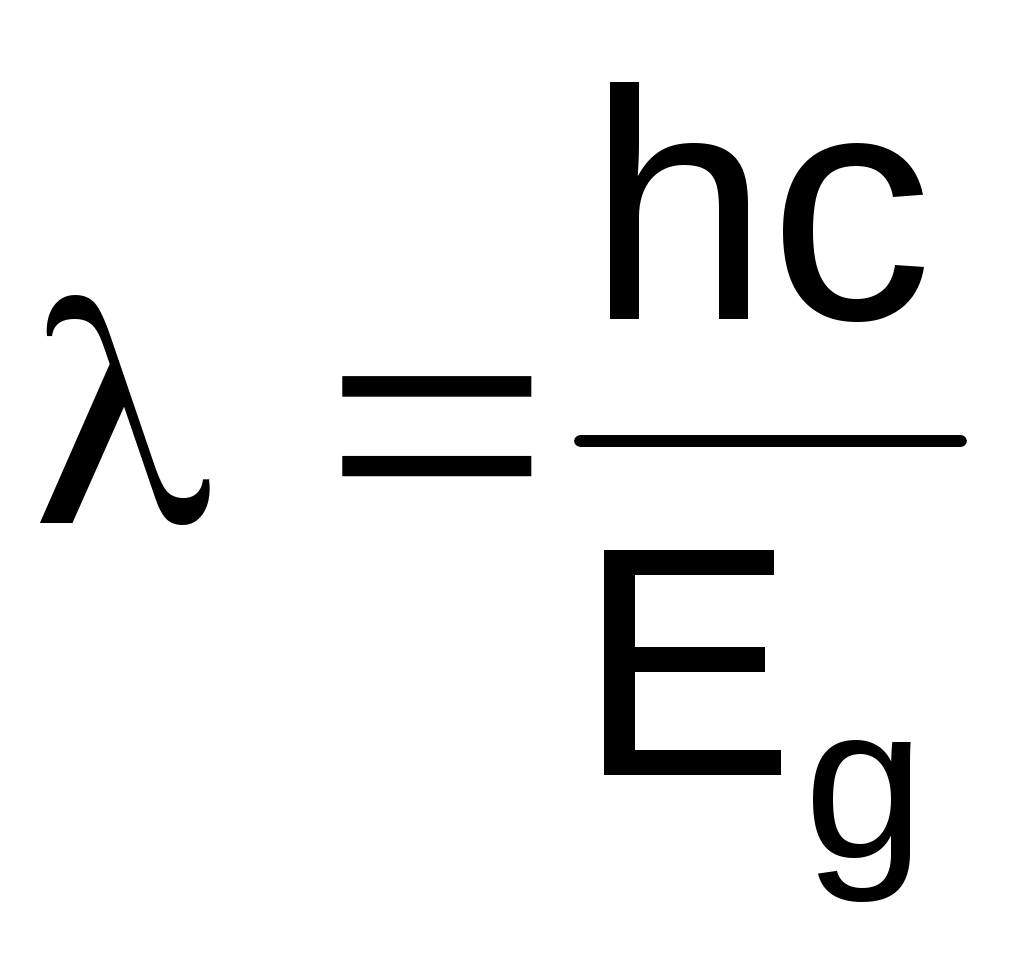 . (4) . (4)
Подставив числовые данные в системе СИ, получим
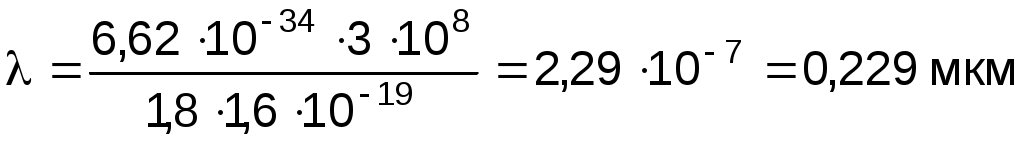 . .
Ответ: = 0,229 мкм.
Задача 2. Небольшая домашняя энергетическая система питается от аккумуляторной батареи, напряжением 12 В, имеющей емкость до 45 Ач. Освещение включается каждый вечер на 4 часа, потребляемый ток 3 А. Какой должна быть фотоэлектрическая энергетическая система, чтобы заряжать аккумуляторную батарею? Как будут соединены солнечные элементы? Световой поток падающий на батарею 1 кВтм-2.
Решение
Для того чтобы зарядить аккумуляторную батарею до 12 В солнечная батарея должна давать напряжение до 15 В. При использовании кремниевого СЭ напряжение на одном элементе при пиковой нагрузке – около 0,5 В. Таким образом, чтобы обеспечить напряжение 15 В, необходимо 15 В/0,5 В = 30 элементов. Так как каждый вечер потребляется 12 Ач электроэнергии, то при КПД аккумулятора 0,8 от СЭ требуется ежедневно 12 Ач / 0,8 = 15 Ач. Пусть элементы освещены Солнцем каждый день в течение 3 часов, тогда требуемый ток составляет 15 Ач/ 3 ч = 5 А. При последовательном соединении такой ток может быть получен с площади 5 А / 210-2 Асм-2 = 250 см2. Тогда на каждый из 30 СЭ приходится площадь 8,33 см2 8,4 см2 (радиус каждого элемента 1,62 см). Таким образом, 30 последовательно соединенных элементов радиусом 1,62 см каждый достаточно для зарядки аккумуляторной батареи в условиях заданного радиационного потока.
Если солнечная батарея работает параллельно с аккумулятором, то необходимо иметь в виду следующее. Каждый модуль обычно состоит из 33 кремниевых фотоэлементов, и такой модуль отдает 1,5 А. Поэтому необходимо 5 А / 1,5 А = 3,33 – округляем до 4. Таким образом, батарея сможет обеспечить ток 6 А. Эти четыре модуля должны быть соединены параллельно. Таким образом, в полной солнечной батарее будет 120 элементов, а общая площадь 1,0 м2 (без учета фактора заполнения).
3.12. Задачи
1. На крыше здания размещены солнечные батареи. Длина крыши L = 40 м, ширина S = 12 м, ЭДС СЭ V0 = 0,5 В. Эффективность СЭ = 210-2 А/см2. Определить экономию электроэнергии летом (время освещения t = 4 часа) и зимой (t = 2,5 часа).
Ответ: 66,12 МДж, 43,2 МДж.
2. Станции полярников для внутренних нужд требуется ежедневно 3 кВтч энергии. Известно, что суммарная площадь СЭ S = 20 м2,
V0 = 0,5 В, эффективность = 210-2 А/см2. Определить суточное время освещения СЭ.
Ответ: 1,5 часа.
3. Группе фермерских хозяйств ежесуточно необходимо 1000 кВтч электроэнергии. Какую площадь должны занимать СЭ при суточном времени освещения СЭ З часа. ЭДС CЭ V0 = 0,5 B, эффективность
= 210 -2А/см2.
Ответ: 3333 м2.
4. Район X имеет следующие среднегодовые солнцеэнергетические ресурсы: мощность светового потока приходящего на 1 м2 – 0,6 кВт; Среднесуточное время освещения имеющегося СЭ 3,5 часа; КПД солнце-энергетической установки = 7%. Какую энергию способна давать солнцеэнергетическая установка при площади коллекторов S = 15 м2 за месяц работы.
Ответ: 238,14 МДж.
5. Карманный калькулятор имеет такие параметры: U = 1,5 В, I = 60 мкА. Определить, каким образом соединены и сколько СЭ (V0 = 0,5 В, = 210-2 А/см2, SСЭ = 1 см2) содержатся в этой батарее.
Ответ: Параллельно 3 ветви из 3 элементов каждая.
6. Для освещения бакенов в течение 12 часов используются лампочки (U = 12 В, Р = 6 Вт). Какую площадь должна занимать солнечная батарея, если rсэ = 2,5 см, V0 = 0,5 В, = 310 А/см2 – при суточном освещении 4,5 часа.
Ответ: 68 элементов займут 1 335 см2.
7. Определить солнечную постоянную G0 вне атмосферы Земли.
Ответ: G0= 1340 Вт/м2.
8. Если Земля характеризуется средней поглощательной способностью , средней излучательной способностью , определить отношение / в случаях, когда равновесная температура равна 10 °С и 25 °С. Диаметр Солнца = 1,389109 м. Диаметр Земли = 1,278107м. Расстояние от Земли до Солнца 1,4981011 м, эквивалентная температура Солнца Ts = 5760 °К.
Ответ: / = 1,08 при Т = 283 °К; / = 1,33 при Т = 298 °К.
9. Ширина запрещенной зоны полупроводника GaAs равна 1,4 эВ. Подсчитайте оптимальную длину волны излучения для фотоэлектрической генерации в СЭ из GaAs.
Ответ: = 0,88 мкм.
10. Записать уравнение вольтамперной характеристики (ВАХ) с р-п–переходом в темноте, если Is = 10-8 Ам2.
Ответ: I = 10-8[ exp (eV / кТ) – 1].
11. При Is = 10-8 Ам2, рассчитать и начертить график ВАХ солнечного элемента до U = 2 В, используя 15…20 точек.
12. Определить отношение средней поглощательной способности к средней излучательной способности /, когда равновесная температура тела равна 30 °С.
Ответ: / = 1,43.
13. Определить значение равновесной температуры, если
/ = 1,16.
Ответ: Т=15 °С.
14. Осветительная система подстанции питается от аккумуляторной батареи напряжением U= 16 В, заряженной до 50 Ач, потребляемый ток I = 5 А. Батарея работает ежедневно 5 часов.
1) Как расположены СЭ? 2) Как собрана электрическая цепь? Дополнительные данные: аккумулятора = 80%, ЭДС СЭ V0 = 0,5 В, суточное время освещения СЭ = 4 часа, эффективность СЭ 2 10-2 А см2.
Ответ: N = 40 штук при последовательном соединении. Площадь солнечной батареи = 781,25 см2. Площадь СЭ = 19,6 см2.
15. Определить температуру кремниевого СЭ, 1КЗ которого увеличивается в 1,08 раза. Облученность СЭ 1 кВт/м2. Первоначальная температура 35 °С.
Ответ: = 161 0С.
16. Во сколько раз изменится мощность кремниевого СЭ при облученности 1 кВт/м2, если собственная температура материала СЭ изменилась от 40 °С до 100 °С.
Ответ: Уменьшится в 1,343 раза.
17. Определить температуру кремниевого СЭ, если его мощность уменьшилась в 1,5 раза. Облучаемость СЭ 1кВт/м2. Первоначальная температура СЭ 45 °С.
Ответ: = 122 °С.
18. Определить мощность солнечной батареи для железнодорожной станции площадью 10 м2, если ЭДС одного элемента
0,45 В. Эффективность в течение дня изменяется по закону:
= 1/1250 (-t2 + 26t – 144).
Ответ: Р = 650 Вт.
19. Определить плотность полного тока через р-n–переход
(без освещения), если плотность тока насыщения для данного СЭ = 10-8 Асм-2 , температура Т = 298 °К V0 = 0,25 В.
Ответ: I =17 мА см2..
20. Аккумулятор заряжается от солнечной батареи, составленной из СЭ: V0 = 0,4 В. Эффективность = 210-2 Асм-2. Время зарядки
6 ч. Напряжение аккумулятора U = 20 В, КПД = 75%,емкость
батареи 30 Ач. Определить параметры солнечной батареи, если
SСЭ = 4 см2.
Ответ: Батарея – 63 параллельно соединенных модулей, каждый из которых состоит из 53 последовательно соединенных заданных элементов.
21. Мощность солнечной батареи при 25 °С 300 Вт, U = 30 В, Батарея составлена из СЭ: V0 = 0,5 В, эффективность = 210-2 Асм-2, SСЭ = 2 см2. Определить параметры батареи, если она собирается при 30 °С.
Ответ: Солнечная батарея из 14 750 СЭ, 250 параллельно соединенных модулей, каждый из которых состоит из 59 последовательно соединенных заданных СЭ.
22. Мощность солнечной батареи при 25 °С равна 250 Вт, ЭДС равна 15 В. Батарея составлена из СЭ V0 = 0,5 В. Эффективность равна = 210-2 Асм-2 , SСЭ = 4 см2. Определить параметры батареи, если она собирается при t = 32 °С.
Ответ: Солнечная батарея из 6225 СЭ; 207 параллельно соединенных модулей, каждый из которых состоит из 97 последовательно соединенных СЭ.
23. Определить во сколько раз изменится V0 кремниевого СЭ, если первоначальная его температура 25 °С, облученность 1 кВт/м2 и его температура: а) 90 °С; б) 110 °С.
Ответ: а) в 0,76 раза; б) в 0,68 раза.
24. Во сколько раз изменится IКЗ солнечной, кремниевой батареи, при нагревании этой батареи до 120 °С, если облученность батареи 1 кВт/м2; первоначальная температура СЭ 50 °С.
Ответ: Увеличится в 1,059 раза.
25. Определить собственную температуру материала солнечного элемента, если произошло понижение V0 в 1,8 раза. Облученность 1 кВт/м2, первоначальная температура кремниевого СЭ t = 40 °С.
Ответ: = 153,4°.
26. Определить мощность солнечной батареи и ее площадь,
если ее ЭДС равна 27 В. Эта батарея составлена из N = 2000 элементов; площадь каждого СЭ 8СЭ = 16 см2 Эффективность (плотность тока)
= 210-2 Асм-2, V0 = 0,5 В.
Ответ: Мощность батареи площадью 3,2м2 равна 320 Вт.
27. Определить энергию, полученную от солнечной батареи за солнечный день. Батарея составлена из N = 3000 СЭ, площадь каждого SСЭ = 12 см2 , V0 = 0,5 В, если эффективность в течение дня изменяется по закону: = 1/2450 (-t2 + 28t – 147).
Ответ: Е= 12,2 МДж.
28. Определить мощность солнечной батареи площадью 2 м2, если ЭДС одного элемента 0,5 В. Эффективность в течение дня изменяется по закону: = 1/2450 (-t2 + 28t – 132).
Ответ: Р = 147 Вт.
29. ЭДС солнечной батареи = 150 В. Мощность 225 Вт. Определить вид соединения СЭ в батарею, если V0 = 0,45 В, эффективность = 1,810-2 Асм-2.
Ответ: Последовательное соединение 334 СЭ площадь каждого 100 см2.
30. Аккумуляторная батарея напряжением 15 В и КПД = 70 % заряжена до 30 Ач, питается от солнечной батареи каждый день в течение 5 часов. Определить параметры солнечной батареи для зарядки аккумулятора в указанный срок, если V0 = 0,4 В. Эффективность СЭ = 210-2 Асм-2 .
Ответ: Требуется 54 последовательно соединенных солнечных батареи, каждая площадью 300 см2.
31. Солнечная батарея мощностью 80 Вт и напряжением 150 В состоит из 4 параллельно соединенных батарей. Определить параметры одной солнечной батареи, если эффективность = 2102 Асм2.
Ответ: Для обеспечения заданных параметров требуются 1040 СЭ, 30 последовательно соединенных блоков, в каждом из которых – 34 параллельно соединенных СЭ.
32. Промышленная солнечная батарея мощностью 60 Вт и напряжением 15 В состоит из трех параллельно соединенных солнечных батарей. Эффективность = 210-2 Асм-2, SСЭ = 1 см2, V0 = 0,5 В, Определить число последовательно соединенных СЭ, количество параллельно включенных блоков, а также общее число солнечных элементов в батарее.
Ответ: Для обеспечения заданных параметров требуется 2010 СЭ; 30 последовательно соединенных блоков, каждый из которых состоит из 67 параллельно соединенных СЭ.
33. Аккумулятор, заряженный от солнечной батареи, составленной из СЭ с V0 = 0,5 В. Эффективность = 210-2 Асм-2, время зарядки 5 ч. Напряжение аккумулятора 16 В. КПД = 80%. Емкость аккумулятора 50 Ач. Определить параметры солнечной батареи, если SСЭ = 2 см2.
Ответ: Батарея – 250 параллельно соединенных модулей, каждый из которых состоит из 40 последовательно соединенных заданных элементов.
34. Мощность солнечной батареи железнодорожной станции при 25 °С равна 500 Вт; Выходное напряжение 50 В, Батарея составлена из СЭ с V0 = 0,4 В. Эффективность = 210-2 Асм-2, SСЭ = 1см2. Определить параметры батареи, если она собирается при температуре 35 °С.
Ответ: Солнечная батарея состоит из 4840 СЭ; 499 параллельно соединенных модулей, каждый из которых 97 последовательно соединенных заданных СЭ.
35. Определить плотность тока через p-n-переход (без освещения), если плотность тока насыщения для данного СЭ I0 = 10-8 Ам-2, а V0 = 0,35 B, T = 290 °K.
Ответ: IД = 12 МА/м2.
36. Солнечная батарея для небольшой железнодорожной станции = 30 В, Р = 400 Вт составлена из СЭ площадью 2 см2. Определить вид соединения солнечных элементов в солнечную батарею, если ЭДС одного СЭ V0 = 0,45 В. Эффективность (плотность тока) = 210-2 Асм-2 .
Ответ: Для обеспечения заданной мощности и напряжения необходимо из 22278 СЭ составить 333 параллельно соединенных блоков, каждый из которых – 67 последовательно соединенных, заданных СЭ.
37. Найти размеры солнечной батареи небольшой железнодорожной станции. Определить количество и размеры СЭ, если ЭДС батареи Е = 220 В, мощность 10 кВт, эффективность СЭ в часы пик = 210-2 Асм-2. ЭДС при типовой нагрузке одного СЭ V0 = 0,45В.
Ответ: Последовательное соединение из 489 СЭ, площадью 0,2275 м2 каждый дает напряжение 220 В и обеспечивает мощность 10 кВт при заданном радиационном потоке.
38. Солнечная батарея (Е = 127 В, Р = 3 кВт) составлена из квадратных СЭ, площадью 4 см2. Определить вид соединения СЭ в солнечную батарею, если ЭДС одного СЭ равна 0,5 В. Эффективность = 210-2 Асм-2.
Ответ: Для обеспечения заданной мощности и напряжения необходимо из 74930 СЭ составить 254 последовательно соединенных заданных СЭ.
39. Определить мощность солнечной батареи, ЭДС которой Е = 110 В и которая составлена из N = 1000 элементов, площадь каждого СЭ равна 25 см2. Эффективность = 210-2 Асм-2, V0 = 0,5 В.
Ответ: Мощность батареи площадью 2,5 м2 составляет Р = 250 Вт.
40. Выходное напряжение солнечной батареи 380 В. Мощность 3 кВт. Определить вид соединения СЭ в батарею, если
V0 = 0,5 В. Эффективность = 210-2 Асм-2.
Ответ: Последовательное соединение 360 СЭ. Площадь каждого равна 315,5 см2.
41. Аккумуляторная батарея напряжением 12В и КПД 80 % заряжена до 40 Ач, питается от солнечной батареи в течение 4 ч. Определить параметры солнечной батареи для зарядки аккумуляторной батареи в указанный срок, если: V0 = 0,3 В. Эффективность СЭ = 210-2 Асм-2 .
Ответ: Требуется 50 последовательно соединенных солнечных батарей, каждая площадью 500 см2.
42. Мощность кремниевой солнечной батареи, при температуре материала 50 °С равна 25 кВт. Определить температуру материала батареи, если ее мощность снизилась до 24,5 кВт. Облученность солнечной батареи 1 кВт/м2.
Ответ: = 55 °С.
43. Определить оптимальную длину волны для фотоэлектрической генерации в солнечном элементе, если ширина запрещенной зоны для материала данного элемента Eg =1,6 эВ.
Ответ: λ = 0,78 мкм.
44. Определить ширину запрещенной зоны для материала СЭ, если оптимальная длина волны излучения для фотоэлектрической генерации в солнечном элементе λ = 1,02 мкм.
Ответ: Eg = 1,23 эВ.
45. Ширина запретной зоны для германия равна 0,6 эВ. Определить оптимальную длину волны для фотоэлектрической генерации в солнечном элементе из Ge.
Ответ: λ = 2 мкм.
46. Ширина запретной зоны для CdTe равна 1,4 эВ. Определить оптимальную длину волны для фотоэлектрической генерации в солнечном элементе из CdTe.
Ответ: λ = 0,89 мкм.
47. Во сколько раз изменится IКЗ солнечной батареи при нагревании этой батареи до 150 °С (облученность батареи 1 кВт·м-2). Первоначальная температура материала 25 °С.
Ответ: В 1,08 раза.
48. Определить собственную температуру материала элемента, если произошло понижение V0 в 2 раза, с учетом, что облученность элемента 1 кВт·м-2 и данный элемент сделан из кремния. Первоначальная температура материала = 25 °С.
Ответ: =160 °С.
49. Определить температуру СЭ, IКЗ которого увеличился в 1,1 раза. Облученность СЭ 1 кВт·м2. Начальная температура данного кремниевого СЭ 25 °С.
Ответ: =181 °С.
50. Первоначальная температура СЭ 25 °С. Его температура изменилась дважды. После первого изменения V0 понизилось в 1,4 раза. После второго изменения IКЗ, по сравнению с первоначальным состоянием, повысился в 1,09 раза. Определить повысилась или понизилась температура кремниевого СЭ после второго изменения по сравнению с первым и на сколько, если облученность СЭ 1 кВт·м2
Ответ: Температура повысилась на 64 °С.
51. Мощность солнечной батареи для питания небольшой станции 5 кВт при температуре 25 °С. Облученность кремниевой солнечной батареи 1 кВтм2 Построить график зависимости мощности данной батареи от температуры в диапазоне 25…150 °С.
52. Во сколько раз изменится мощность кремниевого СЭ, если собственная температура материала СЭ изменилась от 25 °С до 110 °С. Облученность СЭ 1 кВт·м2.
Ответ: Понизится в 1,5 раза.
53. Определить температуру кремниевого СЭ, если его мощность уменьшилась в 1,4 раза. Облученность СЭ 1 кВт·м2. Первоначальная температура СЭ 25 °С.
Ответ: = 96,4 °С.
54. Во сколько раз уменьшится ЭДС кремниевой батареи при увеличении температуры от t 1= 25 °С до t2 =150 °С при облученности 900 Втм2.
Ответ: В 1,86 раза.
55. Во сколько раз увеличится ток короткого замыкания кремниево-солнечной батареи при облученности 900 Вт·м2, если температура её изменяется от t1 =25 °C до12 =200 °С.
Ответ: В 1,11 раза.
56. Вычислить мощность солнечной батареи в условиях облученности 1 кВт·м2 при изменении температуры от t1 = 25 °C до
t2 = 200 °C, если при температуре t = 25 °С ее мощность была
Р = 300 Вт.
Ответ: P(t2) = 99 Вт.
57. Определить плотность тока через р-п-переход (без освещения), если плотность тока насыщения для данного СЭ I0=10 -8 А·м-2, 1) V = 0,3 В; 2) V = 0,4 В (Т = 300 К).
Ответ: 1) ID =1,1 мА·м-2; 2) ID = 52 мА·м-2.
58. Определить во сколько раз изменится V0 кремниевого СЭ, при облученности данного СЭ 1 кВт/м2. Его температура: а) 80 °С; б) 100 °С; в) 120 °С. Первоначальная температура СЭ 25 °С.
Ответ: а) в 0,79 раза; б) в 0,72 раза; в) в 0,64 раза,
59. Ширина запрещенной зоны для кремния Eg = 1,1 эВ. Подсчитать оптимальную длину волны излучения для фотоэлектрической генерации в солнечном элементе из кремния.
Ответ: λ = 1,1З мкм.
60. Ширина запрещенной зоны для CdS равна 2,4 эВ. Определить оптимальную длину волны для фотоэлектрической генерации в солнечном элементе из CdS.
Ответ: λ = 0,52 мкм.
61. Для Ga1-x Alx As (0Eg=l,4-l,9 эВ. Вычислить оптимальную длину волны для фотоэлектрической генерации в солнечной батарее из Ga1-x Al x As при х1 = 0 и х2 = 0,34.
Ответ: λ = 0,88 мкм, λ 2 = 0,65 мкм.
62. Ширина запрещенной зоны для Ga1-x Ai x As при 0,34 < х < 1,0 изменяется от 1,9 эВ до 2,2 эВ. Вычислить оптимальный диапазон длин волн для фотоэлектрической генерации в солнечной батарее из этого полупроводника.
Ответ: λ1 = 0,65 мкм; λ2 = 0,56 мкм.
63. Солнечная батарея имеет площадь 0,5 м2, напряжение холостого хода Uxx = 15 В, ток короткого замыкания IКЗ = 2,5 А. Величина фактора заполнения нагрузочной характеристики равна 0,3. Батарея находится в земных условиях, и на нее падает поток 800 Вт·м-2. Определить величину тока IН при UH = 12 В. Вычислить КПД батареи.
Ответ: IН = 0,94 А, η= 2,8 %.
64. Вычислить мощность солнечной батареи при облученности 900 Вт·м-2 при температуре t = 100 °С и 200 °С, если мощность, отдаваемая ею в нагрузку при t = 25 °С, равна 100 Вт.
Ответ: Р1 = 70 Вт; Р2 = 30 Вт.
65. Солнечное излучение с плотностью потока энергии 0,8 к Вт·м-2 приходит на одиночный кремниевый элемент площадью 100 см2. Пусть 10% фотонов участвуют в генерации электронно-дырочных пар в зоне перехода, ведущей к появлению тока во внешней цепи. Каков будет ток короткого замыкания IКЗ элемента. Нарисовать вольт-амперную характеристику элемента.
Ответ: I = (0,5 · 1021 м-2 с-1 · 2 носитель /фотон) · 10-2 м–2
1,6…10-19 Кл/нос = 1,6 А.
66. Небольшая домашняя осветительная система питается от аккумулятора напряжением 8 В, заряженной до 30 А·ч. Освещение включается каждый вечер на 4 часа, потребляемый ток 3 А.
Какой должна быть фотоэлектрическая энергетическая система, содержащая СЭ, чтобы заряжать аккумуляторную батарею? Как будут соединены солнечные элементы? Как будет собрана электрическая цепь? Как Вы будете проверять цепь и определять КПД. Радиус одного элемента 2,5 см, лучи падают нормально.
Ответ: Если для каждого элемента V = 0,5 В, то при U = 10 В потребуется параллельное соединение 20 последовательных цепочек элементов. Площадь 250 см2.
67. КПД солнечного элемента равен 10%, а радиус солнечного элемента гсэ = 2 см, интенсивность солнечного излучения 1 кВт/м2. Определить: 1) какую мощность вырабатывает батарея, составленная из таких элементов, размещенных на площадке, длина стороны которой 1 м; 2) число солнечных элементов.
Ответ: 1) 78,5 Вт. 2) 625 элементов.
68. "Солнечный пруд" площадью S = 1 км2 дает 60 м горячей воды в сутки с температурой равной 90 °C. Какой площади должен быть солнечный пруд, чтобы обеспечить горячей водой 100 квартирный дом, если каждая семья потребляет около 4 литров горячей воды в час.
Ответ: 160 000 м2.
69. На берегу Апшанского озера в Крыму станция мощностью 5 МВт имеет башню h = 70 м с водяным котлом на вершине. Солнечные лучи концентрируются на стенах котла при помощи зеркал. Зеркала размещаются в чашеобразной выемке диаметром 500 м. Определите мощность, получаемую с квадратного метра поверхности.
Ответ: Р0 = 25,5 Вт.
70. На площадку 6 м2 приходит мощность излучения 6 кВт.
На площадке размещено 9600 солнечных элементов диаметром
d = 2,5 см. Определить КПД СЭ, если известно, что выходная мощность установки 895 Вт.
Ответ: = 19 %.
71. Определите КПД сульфидно-кадмиевого элемента при следующих условиях: г = 2,5 см, V0 = 0,5 В; = 1,6 · 10 -2 А/см2, интенсивность светового потока 1 кВт/м2.
Ответ: = 29 % .
72. Какова эффективность СЭ при облученности 1 кВт/м2, если известно, что КПД такого элемента равен 27 %, V0 = 0,5 В, г = 2,5 см.
Ответ: = 5,4 · 10 -2 А/см2.
73. Определить константу b для тонкопленочного СЭ, если при повышении температуры до 35 °С ток короткого замыкания IКЗ вырос в 1,005 раза.
Ответ: b = 5·10 -4 С -1.
74. Определить до какой температуры нагрели СЭ, если известно, что IКЗ сульфидно-кадмиевого элемента изменился в 1,0638 раза при нагревании этой батареи, а константа b для этого типа элемента равна b = 5,8· 10 -4.
Ответ: t= 135 °С.
75. Мощность первой батареи, состоящей из 5 элементов, соединенных параллельно, равна 250 Вт. Известно также, что три таких же элемента, соединенных последовательно, вырабатывают = 50 В. Определить ток первой батареи.
Ответ: I = 1,66(6) А.
76. Определить схему соединения 20 элементов, если V0 = 0,5 В, I = 0,5 А, Р = 5 Вт.
Ответ: Две параллельных ветви по 10 последовательно соединенных элементов каждая. S = 0,15 м2.
77. Площадь солнечных батарей метеорологического спутника S = 4 м2. Найдите мощность батареи, если КПД равен 15%.
Ответ: Р = 800 Вт.
78. Во сколько раз уменьшится мощность солнечного (кремниевого) элемента при повышении температуры от 0° до 25 °С.
Ответ: В 1,25 раза.
79. Определить константу С для солнечного элемента, если мощность батареи при 25 °С Р = 1 кВт, а при 50 °С – 0,9 кВт. Какому элементу соответствует эта константа?
Ответ: С = 4 · 10 -3 С -1. Кремний.
80. Кремниевый солнечный элемент при 25 °С вырабатывал мощность Р = 1 кВт. При длительном нахождении под прямыми солнечными лучами батарея нагрелась, и мощность ее уже не превышала 0,95 кВт. Определить рабочую температуру батареи.
Ответ: tpaб = 37,5 °С.
81. Под каким углом должна быть наклонена поверхность в 10 часов утра первого февраля, расположенная в Глазго, если угол падения радиации равен = 38,5°, а площадка ориентирована на 20° восточнее направления на юг.
Ответ: Наклонена на 40° к горизонтальной плоскости.
82. На широте 50° в период летнего солнцестояния при
Ghmax = 900 Вт/м2 продолжительность светового дня N = 16 ч. Определить количество энергии, получаемой от солнца за первые четыре часа после восхода.
Ответ: Н = 4,8 МДж.
83. Определить долготу, если локальное солнечное время
tsolar = 10 ч, декретное время tzone = 8 ч, а долгота, на которой находится солнце zone в полдень, равна 30°.
Ответ: 60°.
84. Определить декретное время tzone, если известна долгота = 50°, zone = 25°, а часовой угол = – 30°.
Ответ: 8 часов 20 минут.
85. Определить среднюю температуру Земли Те, если известен радиус Земли R, интенсивность солнечного излучения G0 =1,3 кВт/м, коэффициент отражения р0 = 0,23, излучательная способность Земли =1.
Ответ: Т0 = 250 К = -23 °С.
86. Рассчитать внеатмосферный поток Hоh для = 48° в периоды летнего и зимнего солнцестояний.
Ответ: Летом Hoh = 42,9 МДжм -2;зимой Hoh = 8,2 МДжм -2.
87. Определить угол 2 между направлением потока и вертикалью, а также найти облученность G* = (Gb + Gd), измеренную в направлении потока в Суве ( = -18). В 9 часов утра 20 мая измеренная в горизонтальной плоскости облученность составляет Gh = 1 МДж/м2 в час.
Ответ: 2 = 58°, G* = 0,9 МДж ·ч-1м-2.
88. Вычислить продолжительность дня в периоды летнего и зимнего солнцестояний на широте 12°.
Ответ: 12,7 ч; 11,3 ч.
89. Вычислить продолжительность дня в периоды летнего и зимнего солнцестояний на широте 60°.
Ответ: 18,5 ч; 5,5 ч.
90. Определить поток тепла Ри от приемника с площадью Ар = 15 м2 к теплоносителю при облученности в плоскости приемной площади G = 1 кВт/м2, и эффективности приемника = 60 %.
Ответ: Ри = 9 кВт.
91. Определить продолжительность светового дня 7 ноября в Хабаровске ( = 48,5°).
Ответ: 9,3 часа.
92. Зная, что плотность потока солнечного излучения в момент измерения была h = 450 Вт/м2, продолжительность светового дня 12 часов, а max = 900 Вт/м2, определить, сколько часов прошло с того момента, как встало солнце?
Ответ: 2 часа.
93. В первую половину дня небо было чистым и солнце светило ярко (mах= 900 Вт/м2), во второй половине дня погода испортилась (hmax = 0,5 hmax). Определить суточную облученность одного квадратного метра поверхности солнечной батареи, время освещения N = 16 ч.
Ответ: 22 МДж.
94. Определить продолжительность солнечного дня, если в середине светового дня п = 900 Вт/м2, а через час п = 700 Вт/м2.
Ответ: 4,6 часа.
95. Сравнить энергию, получаемую от солнца в июне, сентябре, январе, если для июня nmax = 900 Вт/м2, N = 16 ч; для сентября – 550 Вт/м2, N = 11,4; для января – 200 Вт/м2, N = 7,2 ч. Построить график зависимости Нп от времени года.
|
|
|
 Скачать 7.49 Mb.
Скачать 7.49 Mb.