Всероссийская олимпиада школьников. ВСЕРОССИЙСКАЯ ОЛИМПИАДА ШКОЛЬНИКОВ. Всероссийская олимпиада школьников по математике. 20172018 уч г. Школьный этап. 8 Класс задания
 Скачать 115.45 Kb. Скачать 115.45 Kb.
|
|
ВСЕРОССИЙСКАЯ ОЛИМПИАДА ШКОЛЬНИКОВ ПО МАТЕМАТИКЕ. 2017—2018 уч. г. ШКОЛЬНЫЙ ЭТАП. 8 КЛАСС Задания (7 баллов) В рамке 8 × 8 шириной в 2 клетки (см. рисунок) всего 48 клеточек. Сколько клеточек в рамке 254 × 254 шириной в 2 клетки?  (7 баллов) В числе 3141592653589793 зачеркните 7 цифр так, чтобы осталось как можно большее число. (7 баллов) Фирма изготавливает лимонный напиток, разбавляя лимонный сок водой. Сначала фирма производила напиток, содержащий 15% лимонного сока. Через некоторое время генеральный директор отдал указание снизить содержание лимонного сока до 10%. На сколько процентов увеличится количество производимого лимонного напитка при тех же объёмах поставок лимонов? (7 баллов) Высоты 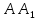 и и 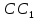 остроугольного треугольника остроугольного треугольника  пересекаются в точке О. Докажите, что если пересекаются в точке О. Докажите, что если  , то треугольник , то треугольник  равнобедренный. равнобедренный.(7 баллов) Малыш и Карлсон поочередно берут конфеты из одного пакета. Малыш берет одну конфету, Карлсон – 2, затем Малыш берет 3 конфеты, Карлсон – 4 и так далее. Когда количество оставшихся в пакете конфет станет меньше необходимого, тот, чья очередь наступила, берет все оставшиеся конфеты. Сколько конфет было в пакете первоначально, если у Малыша в итоге оказалась 101 конфета. (7 баллов) Четыре блохи играют в чехарду на большом листе клетчатой бумаги. Каждую секунду одна из блох перепрыгивает через какую-то другую и, летя над той же прямой, пролетает расстояние, вдвое большее, чем было между блохами до прыжка. Сейчас блохи сидят в четырёх вершинах одной клетки. Могут ли все четыре блохи через некоторое время оказаться на одной прямой? Максимальный балл за все выполненные задания — 42. ВСЕРОССИЙСКАЯ ОЛИМПИАДА ШКОЛЬНИКОВ ПО МАТЕМАТИКЕ. 2016—2017 уч. г. ШКОЛЬНЫЙ ЭТАП. 8 КЛАСС Задания, ответы и критерии оценивания (7 баллов) В рамке 8 × 8 шириной в 2 клетки (см. рисунок) всего 48 клеточек. Сколько клеточек в рамке 254 × 254 шириной в 2 клетки?  Ответ. 2016. Р  ешение. Первый способ. Разрежем рамку на четыре одинаковых прямо- угольника так, как показано на рисунке. Ширина прямоугольников равна ширине рамки, т. е. 2 клетки. Длина каждого прямоугольника на 2 меньше стороны рамки: 254 — 2 = 252 клетки. Тогда площадь одного прямоугольника равна 2 · 252 = 504. А значит, всего в рамке 4 · 504 = 2016 клеток. ешение. Первый способ. Разрежем рамку на четыре одинаковых прямо- угольника так, как показано на рисунке. Ширина прямоугольников равна ширине рамки, т. е. 2 клетки. Длина каждого прямоугольника на 2 меньше стороны рамки: 254 — 2 = 252 клетки. Тогда площадь одного прямоугольника равна 2 · 252 = 504. А значит, всего в рамке 4 · 504 = 2016 клеток.Второй способ. Площадь рамки можно получить, если из площади квадрата 254 × 254 вычесть площадь внутреннего квадрата. Сторона внутреннего квадрата на 4 клетки меньше стороны большого. Значит, площадь рамки равна  Замечание. Если обозначить сторону рамки через n, то можно доказать (например, описанными выше способами), что её площадь будет равна 8n — 16 клеток. (7 баллов) В числе 3141592653589793 зачеркните 7 цифр так, чтобы осталось как можно большее число. Решение: Число тем больше, чем больше цифра старшего разряда. Чтобы число начиналось с 9, на до зачеркнуть первые пять цифр 3141592653589793. Осталось зачеркнуть еще 2 цифры. Зачеркивая 2, получаем на втором месте 6 (больше 6 нам получить не удастся). Чтобы вторая цифра числа была как можно больше, мы можем зачеркнуть только 2. Наибольшей цифрой из возможных на третьем и четвертом местах могут быть 5. Для этого нам надо зачеркнуть 3. Ответ: 965589793. (7 баллов) Фирма изготавливает лимонный напиток, разбавляя лимонный сок водой. Сначала фирма производила напиток, содержащий 15% лимонного сока. Через некоторое время генеральный директор отдал указание снизить содержание лимонного сока до 10%. На сколько процентов увеличится количество производимого лимонного напитка при тех же объёмах поставок лимонов? Ответ: На 50%. Решение: 1 способ. Содержание лимонного сока в напитке после указания генерального директора снизилось в полтора раза. Значит, из тех же лимонов можно приготовить в полтора раза больше лимонного напитка. Иными словами, количество производимого лимонного напитка увеличится в полтора раза или на 50%. 2 способ. Пусть х – количество производимого напитка до указания генерального директора. Тогда количество лимонного сока в этом напитке – 0,15·х. Пусть теперь у – количество производимого напитка после указания генерального директора. Тогда количество лимонного сока в этом напитке – 0,1·у. Так как подразумевается, что количество лимонного сока не изменилось, получаем равенство 0,15·х = 0,1·у. Умножив обе части этого равенства на 10, получим: у = 1,5·х; или: у = х + 0,5·х. Значит, количество производимого напитка увеличилось на 50%. (7 баллов) Высоты 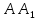 и и 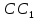 остроугольного треугольника остроугольного треугольника  пересекаются в точке О. Докажите, что если пересекаются в точке О. Докажите, что если  , то треугольник , то треугольник  равнобедренный. равнобедренный.Д  оказательство: оказательство:  по гипотенузе и острому углу. Из равенства треугольников получаем по гипотенузе и острому углу. Из равенства треугольников получаем  , поэтому , поэтому  по катету и острому углу. Откуда получаем по катету и острому углу. Откуда получаем  , то есть , то есть  равнобедренный. равнобедренный.(7 баллов) Малыш и Карлсон поочередно берут конфеты из одного пакета. Малыш берет одну конфету, Карлсон – 2, затем Малыш берет 3 конфеты, Карлсон – 4 и так далее. Когда количество оставшихся в пакете конфет станет меньше необходимого, тот, чья очередь наступила, берет все оставшиеся конфеты. Сколько конфет было в пакете первоначально, если у Малыша в итоге оказалась 101 конфета. Ответ: 211 Решение: Решение: Так как 1+3+5+…+17+19=100, то следует, что Малыш в предпоследний раз взял 19 конфет, а в последний раз – одну оставшуюся конфету. Поэтому первоначально в пакете находилось 1+2+3+4+…+19+20+1=211 (конфет) (7 баллов) Четыре блохи играют в чехарду на большом листе клетчатой бумаги. Каждую секунду одна из блох перепрыгивает через какую-то другую и, летя над той же прямой, пролетает расстояние, вдвое большее, чем было между блохами до прыжка. Сейчас блохи сидят в четырёх вершинах одной клетки. Могут ли все четыре блохи через некоторое время оказаться на одной прямой? Ответ. Нет, не могут. Решение. Предположим, что это случилось, и рассмотрим тот момент, когда все четыре блохи впервые оказались на одной прямой. Попросим ту блоху, которая совершала последний прыжок, прыгнуть обратно. При этом она должна будет снова перелететь через какую-то из других блох вдоль соединяющего их отрезка, т. е. должна будет остаться на той же прямой. Значит, секунду назад все блохи тоже сидели на одной прямой! Но мы рассматривали тот момент, когда четыре блохи впервые оказались на одной прямой. Полученное противоречие доказывает, что наше предположение неверно и все четыре блохи не могли оказаться на одной прямой. Замечание. Другой, более сложный способ решения задачи можно получить, если ввести систему координат, в которой вершины исходного квадрата имеют координаты (0; 0), (0; 1), (1; 0), (1; 1), и разделить все целочисленные точки на четыре типа: те, у которых обе координаты чётны: (Ч; Ч), те, у которых обе нечётны: (Н; Н), и те, у которых чётна только одна из координат: (Ч; Н) и (Н; Ч). Можно точки каждого типа покрасить в свой цвет. Заметим, что при каждом прыжке обе координаты прыгнувшей блохи меняются на чётное число единиц, т. е. чётность координат не меняется. Четыре вершины квадрата имеют разный тип: (Ч; Ч), (Ч; Н), (Н; Ч) и (Н; Н). Однако можно доказать, что на любой прямой встречаются вершины только двух каких-то типов (например, только (Ч; Н) и (Ч; Ч)). Значит, на каждой прямой могут оказаться максимум две блохи (сидевшие вначале в вершинах тех двух типов, которые присутствуют на прямой). Итак, оказывается, что не только четыре, но и три блохи на одной прямой оказаться не могут. Критерии оценивания заданий по математике 8 класс Математическая олимпиада оценивается целым числом баллов от 0 до 7. Итог подводиться по сумме баллов, набранных участником олимпиады.
|
