клапан. Введение 1 Трубопроводная арматура, её применение
 Скачать 3.25 Mb. Скачать 3.25 Mb.
|
5 Расчеты на прочностьРасчет на прочность служит для проверки прочности деталей арматуры и приводов. Пользуясь данными силового расчета по усилиям и моментам, действующим в деталях, определяют величину напряжений в материале деталей и запас прочности. При расчете по методу предельных нагрузок определяется величина наибольшего из допускаемых усилий или моментов. В конструкциях арматуры необходимо обеспечить статическую прочность деталей, поскольку они, как правило, воспринимают статические нагрузки. В этих условиях опасное состояние материала определяется либо возникновением больших остаточных деформаций в пластичных металлах, либо возникновением трещин (разрушение) в хрупких металлах. Соответственно этому при расчете статической прочности деталей критерием прочности пластичных металлов считается предел текучести, а хрупких — предел прочности. В соответствии с первой теорией прочности - теорией наибольших нормальных напряжений — опасное состояние материала возникает в том случае, когда наибольшее по абсолютной величине нормальное напряжение приближается к пределу прочности при растяжении. Исходя из этого, прочность обеспечивается при условии, что σ1 ≤ σдоп Эта теория используется для определения прочности деталей в условиях сложнонапряженного состояния материала, так как она не подтверждается практикой. По второй теории прочности — теории наибольших деформаций — считается, что опасное состояние материала является результатом возникновения относительных деформаций, по величине равных деформациям при достижении предела прочности. Прочность обеспечивается при условии, что σ1-ʋ·(σ2+ σ3) ≤ σдоп Эта теория применима для хрупкого состояния материала. По третьей теории прочности — теории наибольших касательных напряжений — опасное состояние материала возникает при значениях касательных напряжений, которых они достигают при разрушении материала путем растяжения. При растяжении наибольшие касательные напряжения достигают величины полуразности главных растягивающих, поэтому прочность будет обеспечиваться при условии, что Эта теория применима для пластически деформируемых материалов. Четвертая — энергетическая теория прочности признает опасным состояние материала тогда, когда потенциальная энергия деформации, вызывающая изменение формы, достигает определенного предела. Прочность обеспечивается при условии Результаты, получаемые на основании этой теории, хорошо согласуются с практикой. По обобщенной теории прочности Мора нарушение прочности зависит лишь от σ1 и σ3. Пространственная картина напряжений заменяется плоской с изображением круга Мора, построенного на главных напряжениях ах и σ3 в координатах а и т. Графическим путем определяется предельное напряженное состояние и допускаемое напряженное состояние. Явление пластической деформации и разрушение путем среза отражаются хорошо, но явление отрыва отражается неправильно. Эта теория имеет ограниченное применение. Здесь условия прочности выдерживаются при следующей зависимости Объединенная теория Давиденкова — Фридмана учитывает возможные явления разрушения материала как путем отрыва, так и путем сдвига. Учитываются напряженное состояние и свойства материала. Прочность оценивается на основе теории наибольших касательных напряжений и теории наибольших удлинений. При расчете на прочность по этой теории необходимо для каждого из материалов построить диаграмму его механического состояния, учитывающую свойства материала и вид напряженного состояния. Напряженное состояние материала оценивается по отношению наибольшего касательного напряжения к наибольшему растягивающему напряжению в данной точке. 5.1 Расчет корпуса на статическую прочность Расчет на статическую прочность (рис. 5.1 и 5.2) выполнен в соответствии с требованиями Норм АЭУ для режимов НЭ и гидроиспытаний. Задачей расчета на статическую прочность является определение следующих групп категорий напряжений: (σ)1 –приведенные общие мембранные напряжения; (σ)2 –приведенные напряжения, определяемые по суммам составляющих общих или местных мембранных, общих изгибных напряжений; (σ)R –размах приведенных напряжений, определяемый по суммам составляющих общих или местных мембранных, общих и местных изгибных, общих температурных напряжений и напряжений компенсации мембранных, кручения и изгиба. Условия прочности: В режиме НЭ: (σ)1 ≤ [σ]1 = [σ]; (σ)2 ≤ [σ]2 = 1.3·[σ]; (σ)R ≤ [σ]R = min[(2.5-Rp0.2/Rm)·Rp0.2 ;2Rp0.2; Rm); В режиме гидроиспытаний: (σ)1 ≤ [σ]1=1.35·[σ]; (σ)2 ≤ [σ]2 = 1.7·[σ]. Допускаемые напряжения определяются в соответствии с разделом 3 Норм АЭУ. Расчет выполнен МКЭ с использованием программного комплекса ANSYS Workbench. Конечно-элементная модель (далее КЭМ) корпуса представлена на рисунке 5.1.1. Модель образована объемными элементами для решения задач механики деформируемого твердого тела. Результаты расчета приводятся для сечений А-А, Б-Б, В-В и узлов 1, 2, 3, 4 (рисунок 5.3.), в которых определены максимальные величины групп напряжений. В силу симметрии корпуса расчетная модель представляет собой половину. Граничные условия предоставлены на рисунке 5.4 Приложенные нагрузки (рис.5.5): - давление среды в режиме НЭ и гидроиспытаний по таблице 2.1 и разделу 2; - напряжение на торцевой поверхности отрезков трубы (σ)m от действия внутреннего давления; - усилие затяга втулки, приложенное по наружному диаметру внутренней резьбы корпуса (значение усилия по разделу 3); - усилие закрытия по шпинделю, приложенное по диаметру седла корпуса; - расчетное давление Рр и давление гидроиспытаний Рh раздел 2 и таблица 2.1; - момент МВ и сила FВ от веса трубопровода, приложенные к торцам патрубков, принятые по таблице 2.1; - размах момента МР и силы FP от температурной компенсации трубопровода, принятые по таблице 2.1. Моменты учитываются со знаком "плюс" и "минус". Направление моментов выбирается наиболее опасным по условиям прочности. Места приложения нагрузок указаны на рисунке 5.5. Усилие от действия внутреннего давления Qm на свободных концах патрубков, определяемое по формуле: Qm= 0.785·Рр·Dv2 где Dv –внутренний диаметр патрубка. Моменты от трубопровода задаются на торцевых поверхностях в виде изгибающего момента M, который определяется по формуле: М=М/2, где М - изгибающие моменты Мр и Мв. Исходные данные и результаты расчета корпуса представлены в таблице 5.1. 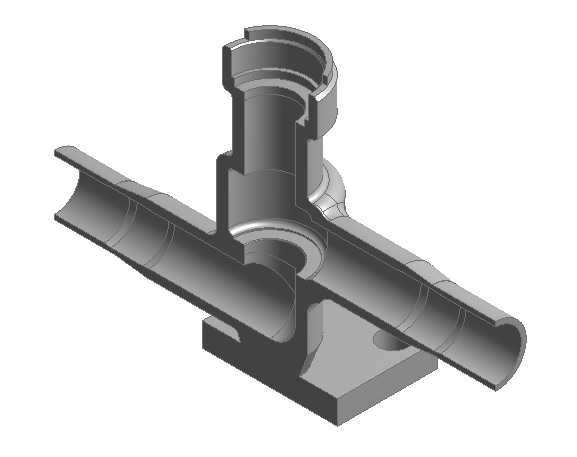 Рис. 5.1 – Твердотельная модель корпуса 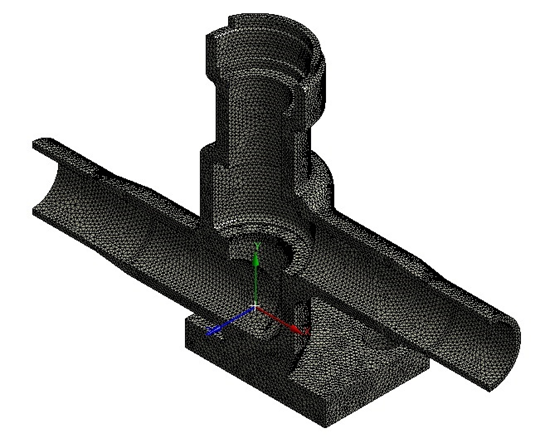 Рис. 5.2 – КЭ модель корпуса 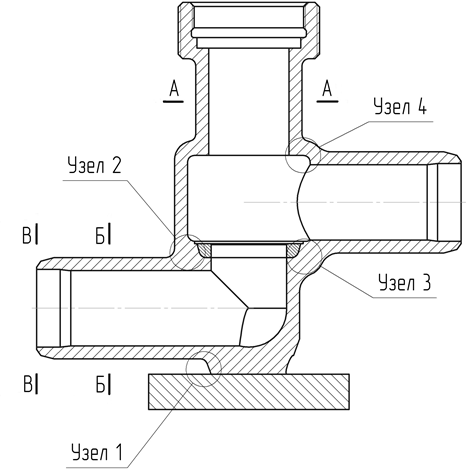 Рисунок 5.3 – Рассматриваемые узлы и сечения корпуса 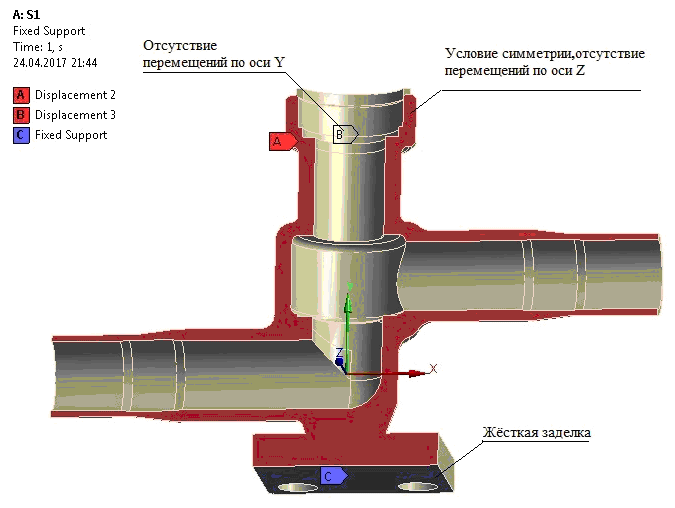 Рисунок 5.4 – Условия закрепления в режиме НЭ 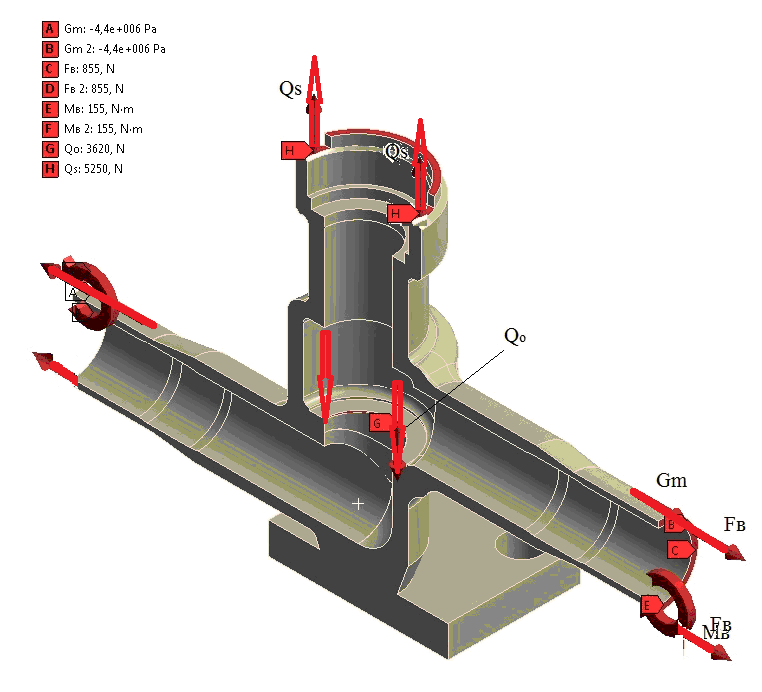 Рисунок 5.5 – Действующие нагрузки в режиме НЭ Таблица 5.1 Расчет корпуса из стали 08Х18Н10Т
5.2 Теплопрочностной расчет корпуса Коэффициент теплоотдачи на внутренней 20000 Вт/(м2 · оС), на наружной поверхности 20 Вт/(м2 · оС). Температуры рабочей среды на внутренней поверхности 220оС; на наружной 20оС. Уравнение конвекции q=hA(Tпов –Токр). Поле распределения температур {Т(хi)} задачи стационарной тепловодности определяется решением уравнения [H]{Т}={Q} . Здесь [H] – матрица коэффициентов теплопроводности, {Т} - вектор температур, {Q} - вектор тепловых нагрузок, формируемый теплопотоками на поверхности, теплоисточниками и конвективной теплопередачей в контактируемую среду. Вычисляется вектор узловых температур в узлах конструкции {Т}. По найденному полю температур решается задача статического нагружения конструкции и определяются узловые перемещения {х}: [К]{x}={F} Здесь [К] – матрица жесткости, а {F} вектор сил, образованный градиентом теплового поля, изменяющего геометрию. В нашем случае система компенсирует тепловые смещения, находясь в составе трубопроводной арматуры. Поэтому напряжения малы и не превышают порядка 3 МПа. 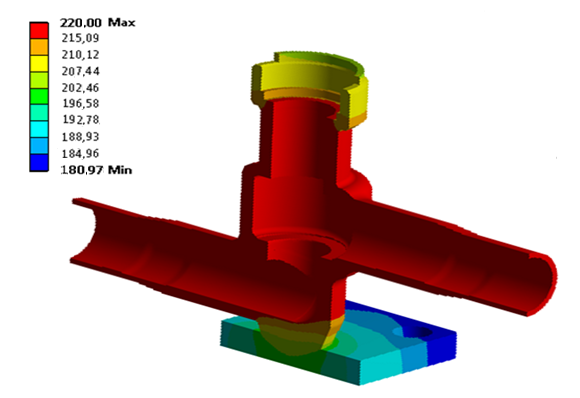 Рис. 5.6 Поле распределения температур 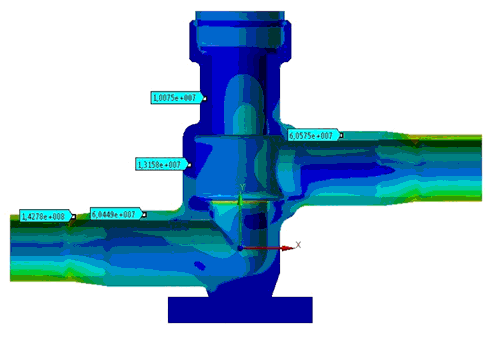 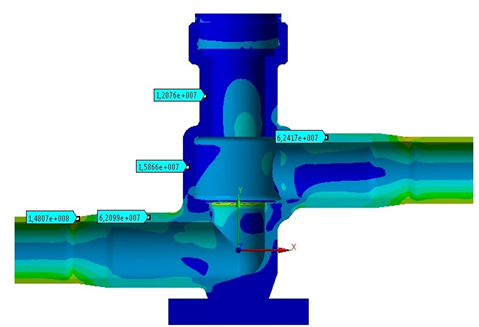 Режим НЭ, σmax= 183 МПа Режим ГИ, σmax= 187 МПа Рис. 5.7 Поле распределения напряжений В расчетах по программе ANSYS использовались объёмные конечные элементы, так как корпус вентиля толстостенный и трехмерный (Рис. 5.1). 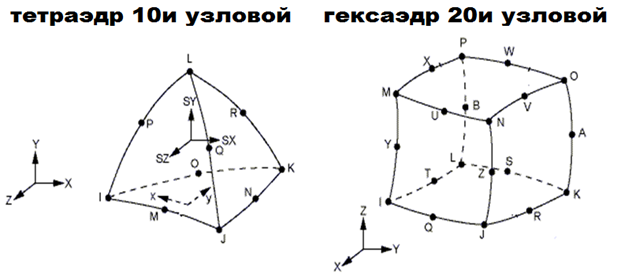 Рис. 5.8 Трехмерные элементы пространства материала корпуса. Изопараметрические элементы Сетка элементов составлена из 10 узловых тетраэдров и 20 узловых гексаэдров (рис. 5.8). Применялись изопараметрические элементы, в которых пространство и искомое поле величин описывается одними функциями формы, здесь квадратичными. Значения напряжений в опасных сечениях корпуса приведены в таблице внизу.
*допускаемое перенапряжение 2% 5.3 Расчет узла золотник-шток на статическую прочность Задачей расчета является определение следующих величин: - (σ)2 – приведенное напряжение в дне золотника, определяемое по сумме составляющих общих мембранных и общих изгибных напряжений (таблица 5.1); - (τ)ср – напряжение среза в штифте (таблица 5.5.2). Условия прочности (Нормы АЭУ, раздел 5, пункт 5.4): Режим НЭ: (σ)2≤ 1.3·[σ] ; (τ)ср ≤ 0.5· [σ]; Режим ННЭ: (σ)2≤ 1.6· [σ], где [σ]- номинальное допускаемое напряжение. Расчет выполнялся программным комплексом ANSYS Workbench в осесимметричной постановке. Конечно-элементная модель, условия закрепления и приложение нагрузок приведено на рисунке 5.5. Значение усилия вдоль шпинделя определяется в разделе 3, берем максимальное значение для электропривода. Контактное давление q определяется по Справочнику машиностроителя под редакцией С.В. Серенсена, Москва 1962г. (том 3, стр.463, случай 5). В качестве напряжения (σ)2 принимается среднее значение приведенного напряжения на нижней поверхности дна золотника на участке до середины стенки. Исходные данные и результаты расчета золотника приведены в таблице 5.2. 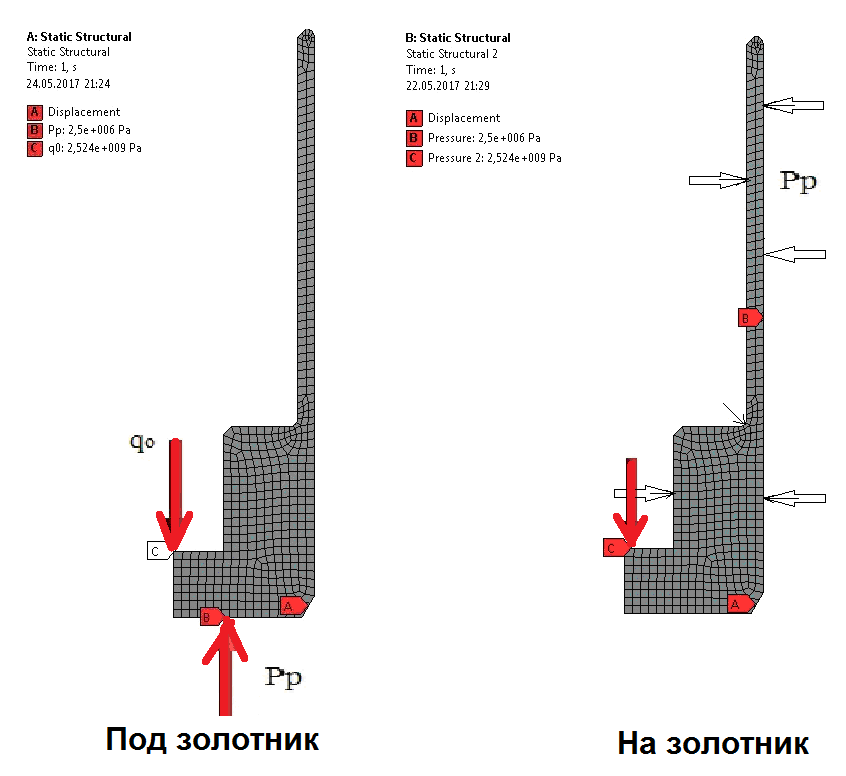 Рисунок 5.9 Расчетная схема  Рис.5.10 Максимальные напряжения max= 1898 МПа
Таблица 5.2 Расчет золотника
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
