кран с лапами. Введение 2 Общие схемы крана, описание устройства, конструкция, работа 3
 Скачать 2.58 Mb. Скачать 2.58 Mb.
|
|
G(1 бл) бл Smax= 2(1 iПЛ) , (3.1.1.3) где G суммарный вес груза, траверсы с лапами и электромагнитом, и штанг, с учетом сил трения, возникающих в штангах; G=341,71 (кН) см. разд. 2.5.1; ηбл КПД подвижных блоков закрепленных на траверсе; ηбл=0,99; iпл кратность полиспаста; iпл=2. Расстояние между соседними витками каната для канатов механизма подъема t=32 (мм) (см. разд. 2.1.3). По формуле 3.1.1.3 Smax= 341,71 (1 0,99) =85,86 (кН). 2(1 0,992 ) По формуле 3.1.1.2 1 88260 325,42 106 2 Ψ=1 186300 0,01 0,032 =0,82. По формуле 3.1.1.1 85,86 103 δ=1,07∙0,82 0,032 127,5 106 =0,0185 (м); Принимаем δ=20 (мм). Необходимо проверить устойчивость цилиндрической части барабана по формуле (см. форм. 5.5 [8]) n= к н >[n], (3.1.1.4) где n запас устойчивости; допускаемое его значение для стальных барабанов [n]≥1,7; ζн номинальное напряжение в цилиндрической стенке, МПа; ζк критическое напряжение, МПа. Номинальное напряжение (см. форм. 5.5 [8]) ζн= Smax ; (3.1.1.5) t ζн= 85,86 0,02 0,032 =134,16 (МПа). Критическое напряжение 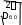 ζк=0,92∙Eб∙ , (3.1.1.6) ζк=0,92∙Eб∙ , (3.1.1.6)lт где lт расстояние между торцевыми стенками, м; lт=600 (мм). 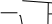 ζк=0,92∙186300∙106 ∙ 0,02 ζк=0,92∙186300∙106 ∙ 0,020,6 2 0,02 =1356,9 (МПа). 0,71 Полученное значение не должно быть более ζк=0,8ζт; для стали ВСт3сп ζт=245 (МПа). ζк=0,8∙245=196 МПа. В расчетах используем ζк=196 МПа. По формуле 3.1.1.4 n= 196 0,82 134,16 =1,78. При длине барабана L<3Dб0 цилиндрическую стенку следует проверить на действие кручения. ζк= Тк Wэ ≤[ζ]к, (3.1.1.7) где Тк крутящий момент, Н∙м; Wэ экваториальный момент сопротивления, м3. Крутящий момент на барабане равен Тк=(S1+S2)∙Dбп/2, (3.1.1.8) где S1, S2 натяжения в ветви каната подъема и управления соответственно; S1=75,68 (кН), S2=20,21 (кН) (см. разд. 2.5.1); Dбп диаметр барабана, м; Dбп=739 (мм) (см. разд. 2.1.3). Тк=(75,68+20,21)∙0,739/2=35,44 (кН∙м). Экваториальный момент сопротивления сечения (D4 (D 2 )4 ) Wэ= б0б0 32 Dб0 3,14 (0,714 (0,71 2 0,02)4 ) Wэ= 32 0,710 =0,0073 (м3). (3.1.1.9) По формуле 3.1.1.7 35,44 103 ζк= 0,0073 =4,85 (МПа) Расчет узла крепления каната к барабану Канат к барабану крепится прижимными планками (см. рис. 3.1.2.1). Согласно правилам ГГТН, число болтов прижимной планки должно быть не менее двух. Необходимое число болтов (см. форм. 5.7 [8]) d z= 1,3kP Pf1lk , (3.1.2.1) 2 1 [ ] р4 [ ] р0,1d 3 где k коэффициент запаса надежности крепления каната к барабану; k≥1,5; P суммарное усилие растяжения болтов, Н; f1 приведенный коэффициент трения между канатом и поверхностью планки; l расстояние от дна канавки на барабане до верхней плоскости прижимной планки, м; l=39 (мм) (см. рис. 3.1.2.1); [ζ]р допускаемые напряжения растяжения в болте; для стали Ст.3 [ζ]р=117 МПа; d1 диаметр болта, м. 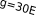  Рис. 3.1.2.1. Прижимная планка. Рис. 3.1.2.1. Прижимная планка.Суммарное усилие растяжения болтов, прижимающих канат к барабану (см. форм. 5.6 [8]) P= 2Smax , (3.1.2.2) 1 2ff f sin 1(e 1)e где f=0,1 коэффициент трения между канатом и барабаном; γ угол наклона боковой грани трапециевидного выреза в планке к вертикали; γ=300 (см. рис. 3.1.2.1); α угол обхвата барабана неприкосновенными витками; α=3π; е основание натурального логарифма. P= 1 2 85,86 23,140,1 0,133,14 =77,17 (кН). 0,1 sin 300 1 (2,73 1) 2,73 Приведенный коэффициент трения между канатом и поверхность планки f1= f; (3.1.2.3) sin f1= 0,1 sin 300 =0,2. Принимаем болт М36, тогда необходимое число болтов для крепления каната подъема (см. форм. 3.1.2.1) 1,3 1,5 77,17 103 z= 6 3,14 0,0362 77,17 103 0,2 0,04 1,5 117 106 0,1 0,0363 =3. l=40 117 10 4 Суммарное усилие растяжения болтов, прижимающих канат управления к барабану (см. форм. 3.1.2.2) P= 1 2 20,21 23,140,1 0,133,14 =18,17 (кН). 0,1 sin 300 1 (2,73 1) 2,73 Считаем длину l=23,5 (мм). Принимаем болт М16, тогда необходимое число болтов для крепления каната управления (см. форм. 3.1.2.1) 1,3 1,5 18,17 103 z= 6 3,14 0,0182 18,17 103 0,2 0,0235 1,5 117 106 0,1 0,0183 =3. 117 10 4 Расчет оси барабана Для компенсации несоосности опор ось барабана помещается на самоустанавливающихся сферических двухрядных роликовых подшипниках. Нагрузки на ступицы барабана (при пренебрежении его весом), для случая, когда груз опущен, найдем из уравнений моментов (см. рис. 3.1.3.1): ΣМАi=0; Smax∙l1+Smax2∙(lн2+lгл+lн1+l1)-P2∙(lн2+lгл+lн1+l2+l1)=0, отсюда P2= |
