|
|
Введение Основные определения Основные пояснения и термины
3. Анализ электрических цепей постоянного тока
с одним источником энергии 3.1. Расчет электрических цепей постоянного тока
с одним источником методом свертывания
В соответствии с методом свертывания, отдельные участки схемы упрощают и постепенным преобразованием приводят схему к одному эквивалентному (входному) сопротивлению, включенному к зажимам источника. Схема упрощается с помощью замены группы последовательно или параллельно соединенных сопротивлений одним, эквивалентным по сопротивлению. Определяют ток в упрощенной схеме, затем возвращаются к исходной схеме и определяют в ней токи.
Рассмотрим схему на рис. 3.1. Пусть известны величины сопротивлений R1, R2, R3, R4, R5, R6, ЭДС Е. Необходимо определить токи в ветвях схемы. .
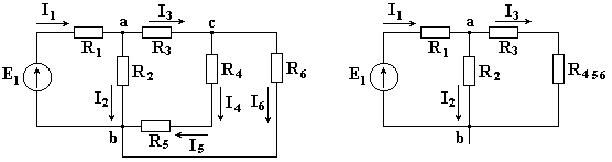
Рис. 3.1 Рис. 3.2 Сопротивления R4 и R5 соединены последовательно, а сопротивление R6 - параллельно с ними, поэтому их эквивалентное сопротивление
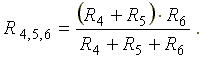
После проведенных преобразований схема принимает вид, показанный на рис. 3.2, а эквивалентное сопротивление всей цепи
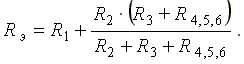
Ток I1 в неразветвленной части схемы определяется по формуле:
Найдем токи I2 и I3 в схеме на рис. 3.2 по формулам:
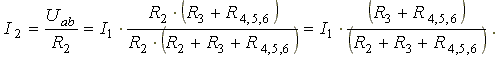
I3 = I1 - I2 - формула получается из уравнения, составленного по первому закону Кирхгофа:
I1 - I2 - I3 = 0.
Переходим к исходной схеме на рис. 3.1 и определим токи в ней по формулам:
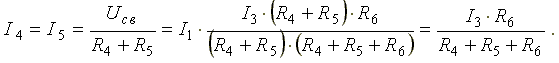
I6 = I3 - I4 (в соответствии с первым законом Кирхгофа I3 - I4 - I6 =0).
4. Анализ сложных электрических цепей с несколькими источниками энергии 4.1. Метод непосредственного применения законов Кирхгофа
На рис. 4.1 изображена схема разветвленной электрической цепи. Известны величины сопротивлений и ЭДС, необходимо определить токи.
В схеме имеются четыре узла, можно составить четыре уравнения по первому закону Кирхгофа. Укажем произвольно направления токов. Запишем уравнения::
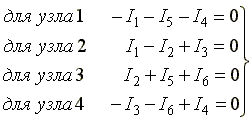 (4.1) (4.1)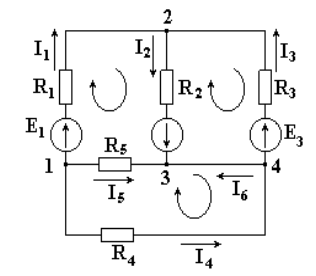
Рис. 4.1
Сложим эти уравнения. Получим тождество 0 = 0. Система уравнений (4.1) является зависимой.
Если в схеме имеется n узлов, количество независимых уравнений, которые можно составить по первому закону Кирхгофа, равно n - 1.
Для схемы на рис. 4.1 число независимых уравнений равно трем.
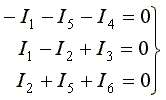 (4.2) (4.2)
Недостающее количество уравнений составляют по второму закону Кирхгофа. Уравнения по второму закону составляют для независимых контуров. Независимым является контур, в который входит хотя бы одна новая ветвь, не вошедшая в другие контуры.
Выберем три независимых контура и укажем направления обхода контуров. Запишем три уравнения по второму закону Кирхгофа.
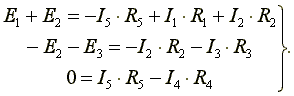 (4.3) (4.3)
Решив совместно системы уравнений (4.2) и (4.3), определим токи в схеме.
Ток в ветви может иметь отрицательное значение. Это означает, что действительное направление тока противоположно выбранному нами.
Метод непосредственного применения законов Кирхгофа громоздок. Имеется возможность уменьшить количество совместно решаемых уравнений системы. Число уравнений, составленных по методу контурных токов, равно количеству уравнений, составляемых по второму закону Кирхгофа.
Метод контурных токов заключается в том, что вместо токов в ветвях определяются, на основании второго закона Кирхгофа, так называемые контурные токи, замыкающиеся в контурах.
На рис. 4.2 в качестве примера изображена двухконтурная схема, в которой I11 и I22 - контурные токи.
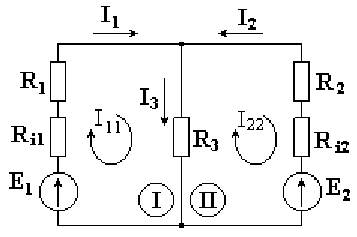
Рис. 4.2
Токи в сопротивлениях R1 и R2 равны соответствующим контурным токам. Ток в сопротивлении R3, являющийся общим для обоих контуров, равен разности контурных токов I11 и I22, так как эти токи направлены в ветви с R3 встречно.
|
|
|
 Скачать 5.72 Mb.
Скачать 5.72 Mb.